[Python] 버블 정렬, 선택 정렬, 삽입 정렬

버블 정렬

인접한 원소들을 비교하고 필요에 따라 위치를 교환하는 방식이다. 큰 값(또는 작은 값)이 배열을 통해 버블(거품)처럼 서서히 상단(또는 하단)으로 이동하며 정렬한다.

1. 배열의 처음부터 끝까지 순회를 시작한다.
2. 현재 원소와 바로 다음에 있는 원소를 비교. 정렬하려는 순서(오름차순 또는 내림차순)에 따라, 현재 원소가 다음 원소보다 크거나(오름차순 정렬) 작다면(내림차순 정렬), 두 원소의 위치를 교환한다.
3. 배열의 모든 원소에 대해 이 과정을 반복한다. 한 번의 순회로 가장 큰(또는 가장 작은) 원소가 배열의 끝으로 이동한다.
4. 배열에 더 이상 교환할 원소가 없을 때까지, 또는 정렬이 완료될 때까지 전체 과정을 반복한다.

💡 특징

• 최악의 경우와 평균적인 경우 모두 (O(n^2))의 시간 복잡도를 가짐.
• 공간 복잡도 (O(1))의 추가 공간을 사용.
• 동일한 값을 가진 원소의 상대적인 순서가 정렬 후에도 유지되서 안정적임.
• 대규모 데이터에서는 상대적으로 비효율적이나 작은 데이터셋이나 거의 정렬된 데이터셋에 대해서는 효율적임.

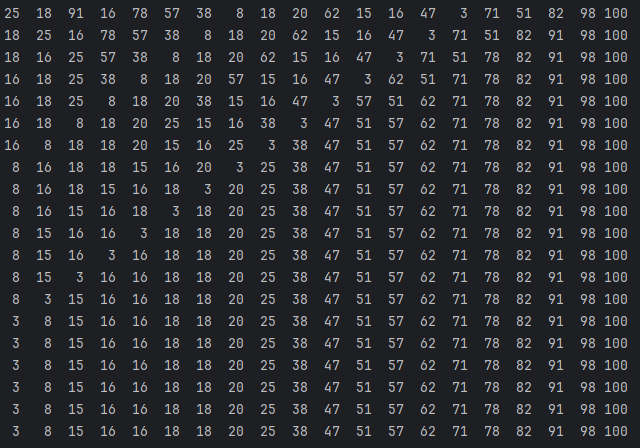
def bubble_sort(arr):
    n = len(arr)
    for i in range(n):
        for j in range(0, n-i-1):
            if arr[j] > arr[j+1]:
                arr[j], arr[j+1] = arr[j+1], arr[j]
    return arr

# 예시 배열
arr = [64, 34, 25, 12, 22, 11, 90]
bubble_sort(arr)
print("Sorted array is:", arr)

선택 정렬

전체 배열을 순회하며 각 위치에 올바른 값을 찾아서 배치하는 방식이다.

1. 배열 전체에서 최소값을 탐색한다.
2. 최소값을 배열의 현재 위치와 교체하고 첫 번째 위치에서 시작한다.
3. 현재 위치를 한 칸 옮기고 남은 배열에 대해 최소값을 다시 탐색한다.
4. 배열의 모든 요소가 올바르게 정렬될 때까지 반복한다.

💡 특징

• 배열의 크기가 n일 때, 약 n(n-1)/2번의 비교가 이루어짐. ->시간 복잡도가 O(n^2)
• 교환 횟수가 적음. 최악의 경우에도 n-1번의 교환만을 수행함.
• 값이 같은 레코드가 입력에 있을 경우, 그 순서가 정렬 후에도 유지되지 않을 수 있기 때문에 안정적이지 않음.
• 추가적인 메모리 공간을 거의 사용하지 않음.

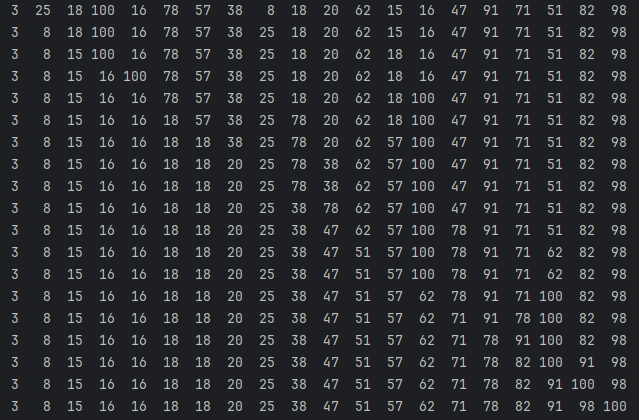
def selection_sort(arr):
    n = len(arr)
    for i in range(n):
        min_idx = i
        for j in range(i+1, n):
            if arr[j] < arr[min_idx]:
                min_idx = j
        arr[i], arr[min_idx] = arr[min_idx], arr[i]
    return arr

삽입 정렬

각 반복에서 하나의 데이터를 적절한 위치에 삽입함으로써 작업을 수행한다. 이미 정렬된 부분과 정렬되지 않은 부분으로 배열을 나누고, 정렬되지 않은 부분의 각 요소를 차례대로 이미 정렬된 부분의 적절한 위치에 삽입하는 방식으로 작동한다.

1. 배열의 두 번째 요소부터 시작하여, 해당 요소가 삽입될 적절한 위치를 이미 정렬된 배열 부분에서 찾는다.
2. 선택된 요소를 그보다 큰 모든 요소 뒤로 이동시킨 후, 적절한 위치에 삽입한다.
3. 정렬이 완료될 때 까지 반복한다.

💡 특징

• 동일한 값을 가진 요소의 상대적 순서가 변경되지 않아 안정적이다.
• 공간 복잡도 O(1)의 추가 메모리만을 사용한다.
• 시간 복잡도는 최선의 경우 O(n), 평균 및 최악의 경우 O(n^2)이다.
• 배열이 이미 정렬되어 있으면 빠르게 작동하지만, 역순으로 정렬되어 있거나 무작위일 때는 느리다.
• 작은 데이터 세트에 대해 사용하거나, 거의 정렬된 배열을 정렬할 때 효율적이다.

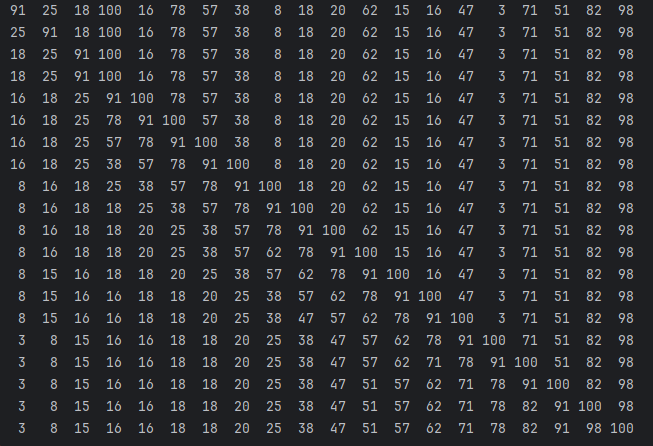
def insertion_sort(arr):
    for i in range(1, len(arr)):
        key = arr[i]
        j = i-1
        while j >= 0 and key < arr[j]:
            arr[j + 1] = arr[j]
            j -= 1
        arr[j + 1] = key

# 예시 배열
arr = [12, 11, 13, 5, 6]
insertion_sort(arr)
print("정렬된 배열:", arr)