[Python] 퀵 정렬, 병합 정렬, 기수 정렬

퀵 정렬

평균적으로 매우 빠른 실행 시간을 가지는 비교 기반 정렬 알고리즘이다. 분할 정복(divide and conquer) 방식을 통해 큰 문제를 작은 문제로 나누어 해결한다. '피벗(pivot)'을 사용하여 배열을 분할하는 것이 핵심이며, 피벗을 기준으로 피벗보다 작은 모든 요소는 피벗의 왼쪽에, 큰 모든 요소는 피벗의 오른쪽에 위치하도록 배열을 재배치한다.

1. 배열에서 하나의 요소를 피벗으로 선택한다. (첫 번째, 마지막, 중간, 무작위 등)
2. 선택된 피벗을 기준으로 배열을 좌우로 분할. 피벗보다 작은 모든 요소는 피벗의 왼쪽에, 피벗보다 큰 모든 요소는 피벗의 오른쪽에 오도록 한다. -> 피벗 스스로는 정렬된 상태가 됨.
3. 피벗을 제외한 왼쪽 부분과 오른쪽 부분 각각에 대해 재귀적으로 위의 과정을 반복.

💡 특징

• 평균적으로 매우 빠른 실행 시간(O(n log n))을 가짐.
• 추가적인 메모리 사용이 거의 없으며, 제자리 정렬(in-place sorting)이 가능함.
• 대규모 데이터셋에 대해 효율적으로 작동하며, 자주 사용됨. -> 재귀적 접근을 하기 때문에 재귀의 깊이가 깊어질수록 처리해야 할 데이터의 양이 줄어들기 때문
• 피벗 선택이 불균형적으로 이루어졌을 때 최악의 경우 시간 복잡도가 O(n^2)까지 증가할 수 있음.
• 안정 정렬이 아니기 때문에, 동일한 값을 가진 요소의 원래 순서가 유지되지 않을 수 있음.

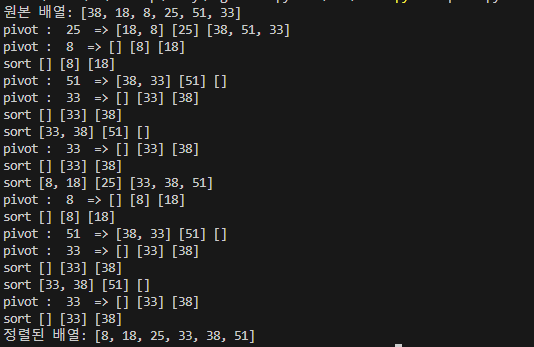
def quickSort(arr):
    if len(arr) <= 1:
        return arr
    pivot = arr[len(arr) // 2]
    left = [x for x in arr if x < pivot]
    middle = [x for x in arr if x == pivot]
    right = [x for x in arr if x > pivot]
    return quickSort(left) + middle + quickSort(right)

# 예시 배열
arr = [3, 6, 8, 10, 1, 2, 1]
sorted_arr = quickSort(arr)
print("정렬된 배열:", sorted_arr)

병합 정렬

분할 정복(Divide and Conquer) 알고리즘으로, 큰 문제를 작은 문제로 나눈 뒤 각각 해결한 다음 결과를 합쳐 전체 문제의 답을 얻는 방법이다. 평균적으로 O(n log n)의 시간 복잡도를 가지며, 안정적인 정렬 방법으로 동일한 값을 가진 원소의 상대적인 순서가 변경되지 않는다.

1. 정렬되지 않은 리스트를 계속해서 절반으로 나누어, 각 부분 리스트의 크기가 1이 될 때까지 분할한다.
2. 각각의 부분 리스트를 재귀적으로 정렬한다.
3. 정렬된 부분 리스트들을 하나의 정렬된 리스트로 병합한다.

💡 특징

• 분할 정복 전략을 사용하여 O(n log n)의 시간 복잡도를 가짐.
• 재귀 호출을 사용하기 때문에, 시스템의 스택 크기가 큰 데이터를 정렬할 때 제한적일 수 있음.
• 분할된 리스트를 합치는 과정에서 추가적인 메모리 공간이 필요함. -> 매우 큰 데이터셋을 다룰 때는 메모리 사용량을 고려해야 함.
• 적은 양의 데이터에 대해서는 삽입 정렬이나 버블 정렬과 같은 간단한 정렬 알고리즘이 더 효율적일 수 있음.

def merge_sort(arr):
    if len(arr) > 1:
        mid = len(arr)//2
        L = arr[:mid]
        R = arr[mid:]

        merge_sort(L)
        merge_sort(R)

        i = j = k = 0

        while i < len(L) and j < len(R):
            if L[i] < R[j]:
                arr[k] = L[i]
                i += 1
            else:
                arr[k] = R[j]
                j += 1
            k += 1

        while i < len(L):
            arr[k] = L[i]
            i += 1
            k += 1

        while j < len(R):
            arr[k] = R[j]
            j += 1
            k += 1

    return arr

# 예시 데이터를 사용한 정렬
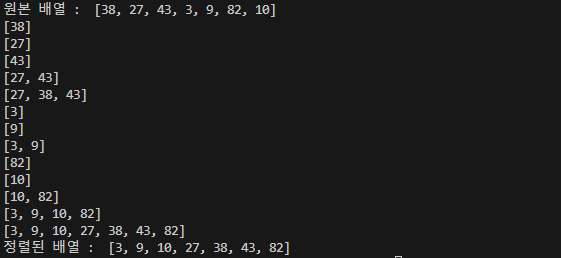
arr = [38, 27, 43, 3, 9, 82, 10]
sorted_arr = merge_sort(arr)
print(sorted_arr)

기수 정렬

데이터의 자릿수나 문자의 위치를 기준으로 그룹을 나누어 정렬한다. 특히 정수를 정렬할 때 효율적이며, 내부적으로 안정적인 카운팅 정렬(Counting Sort)이나 버킷 정렬(Bucket Sort)을 사용하여 각 자릿수별로 정렬을 수행한다. 기수 정렬의 시간 복잡도는 O(nk)로, n은 정렬할 원소의 수, k는 원소의 최대 자릿수를 의미한다.

1. 가장 낮은 자릿수부터 시작하여 가장 높은 자릿수까지 순차적으로 정렬을 수행.
2. 각 자릿수에 대해 안정적인 정렬 알고리즘(예: 카운팅 정렬)을 사용하여 정렬.
3. 모든 자릿수에 대한 정렬이 완료되면, 전체 데이터가 정렬된다.

💡 특징

• 숫자와 같은 특정 유형의 데이터에만 적용됨.
• 추가적인 메모리 공간을 요구함.
• 성능은 자릿수의 길이(k)에 크게 의존하기 때문에 매우 큰 숫자를 정렬할 때는 성능 저하가 발생할 수 있음.

def counting_sort(arr, exp1):
    n = len(arr)
    output = [0] * n
    count = [0] * (10)

    for i in range(0, n):
        index = arr[i] // exp1
        count[index % 10] += 1

    for i in range(1, 10):
        count[i] += count[i - 1]

    i = n - 1
    while i >= 0:
        index = arr[i] // exp1
        output[count[index % 10] - 1] = arr[i]
        count[index % 10] -= 1
        i -= 1

    for i in range(0, len(arr)):
        arr[i] = output[i]

def radix_sort(arr):
    max1 = max(arr)
    exp = 1
    while max1 // exp > 0:
        counting_sort(arr, exp)
        exp *= 10

arr = [170, 45, 75, 90, 802, 24, 2, 66]
radix_sort(arr)
print(arr)