딥러닝 특화 과정을 수강하고 러닝을 정리합니다.

Convolutional Neural Networks

CNN의 레이어(컨볼루션,풀링)을 학습하고 다중분류문제 해결을 위한 심층신경망 모델을 구현해본다.

• Convolution operation, Pooling operation
• CNN에서 사용되는 용어 (Padding, Stride, filter, channel, ...)
• Advantages of Conv layer
• CNN 모델 훈련 과정

Computer Vision

• 활용 분야 : 이미지 분류, 객체 탐지, 신경망 전이학습
• 입력 데이터가 크다.
  • cat non-cat 분류 실습에서 사용된 저해상도의 이미지(3 color channels)는 input feature가 64*64(*3) → 12288의 크기를 가졌다.
  • 고해상도의 이미지(1mega pixel) 1000*1000(*3) → 3millions 크기를 가진다.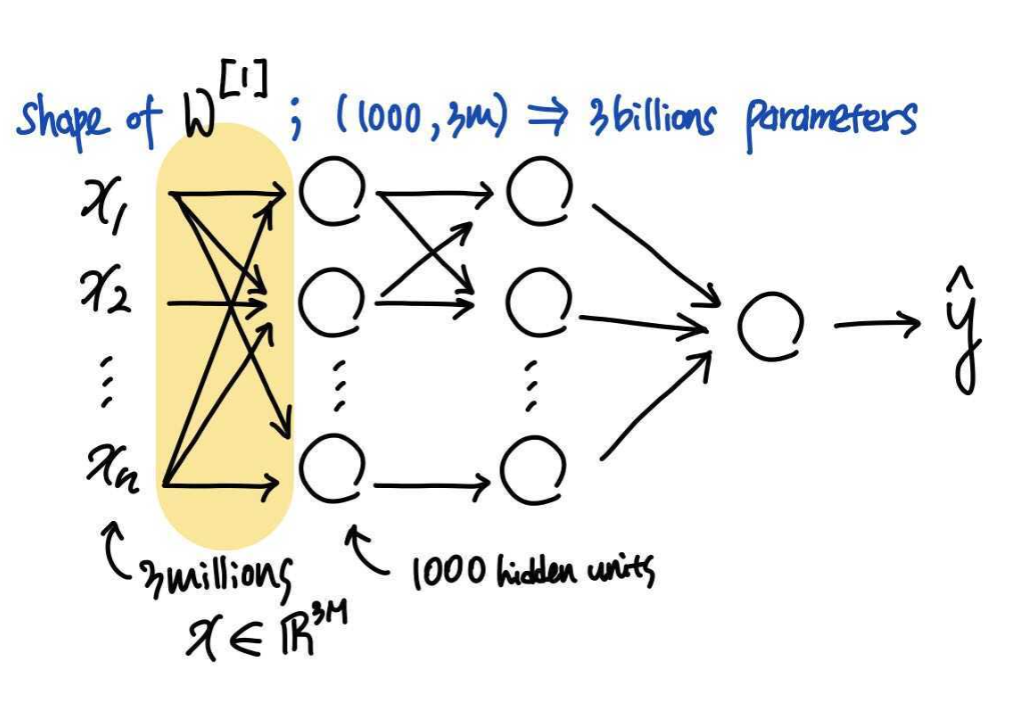 이러한 input feature와 첫번째 은닉레이어에 1000개의 은닉유닛이 있다고 가정하면, $W^{[1]}$이 (1000,3millions) 형태가 되고, 30억개의 모수를 가지게 되는 것이다.
  • 모수가 이렇게 많으면 충분한 데이터를 얻어 과적합을 방지하는 것이 어렵고, 연산과 메모리에 대한 부담이 있을 수 있다.

## Edge Detection Example ### Computer Vision Problem  ConvolutionNN에서는 하위층(earlier layers)가 **윤곽선을 감지** → 이후의 레이어들이 가능성있는 물체를 감지 → 더 이후의 층들이 온전한 물체의 부분을 감지한다.

📍 Convolution Operation

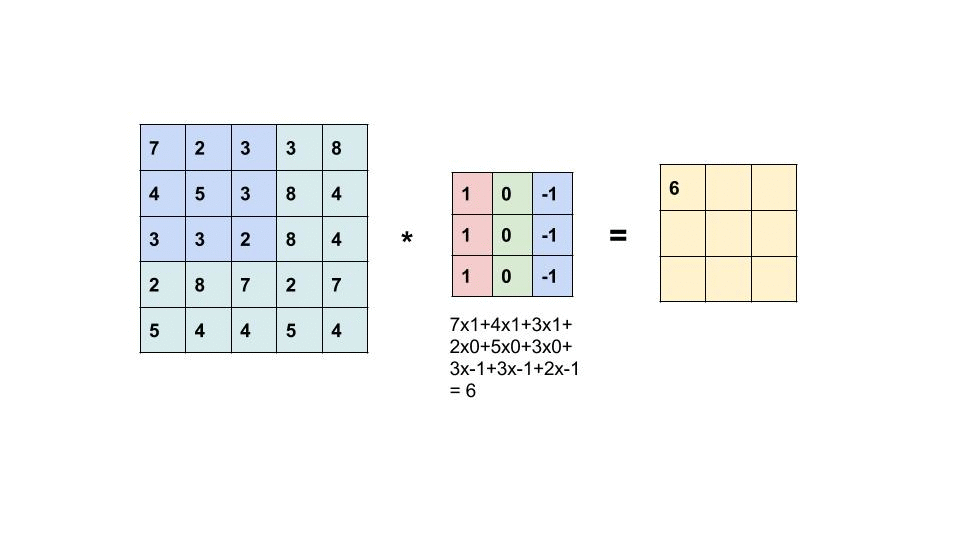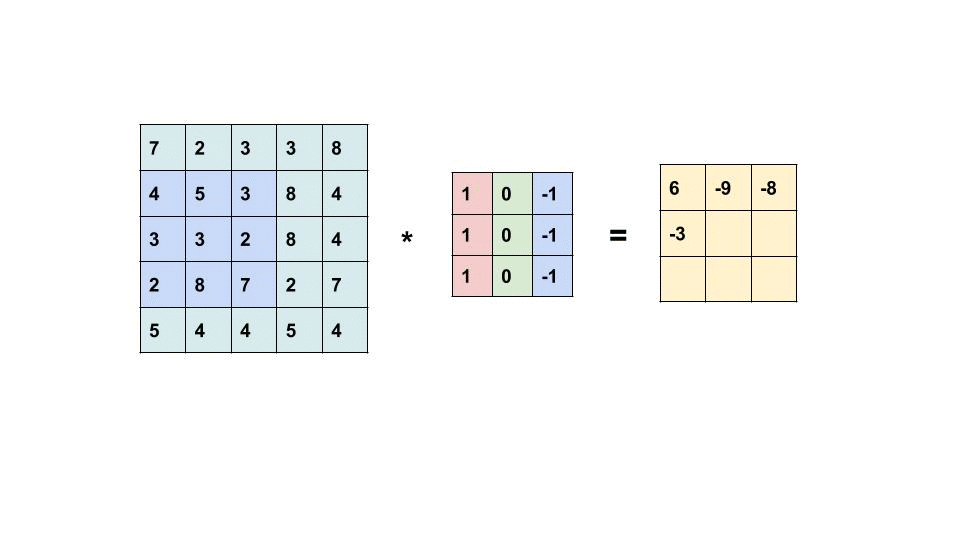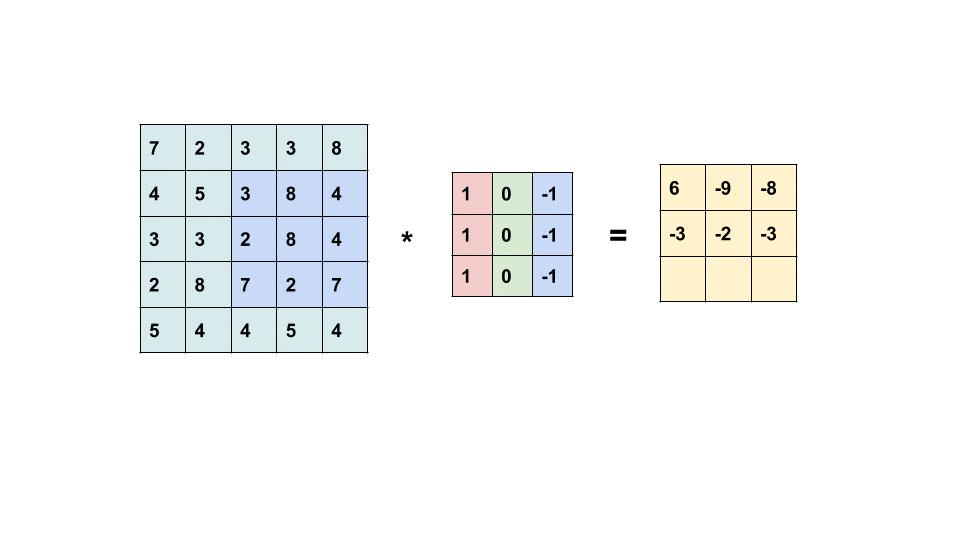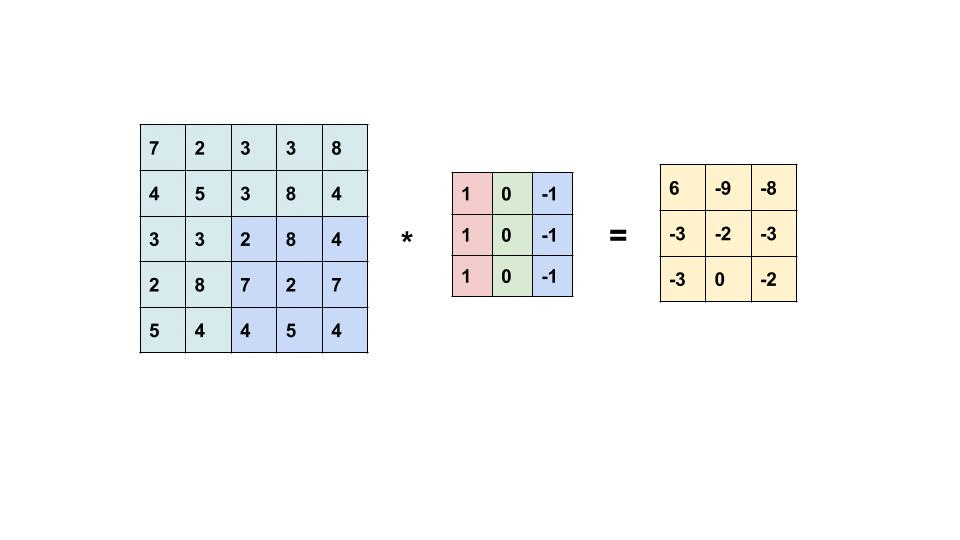
Convolution layer는 Convolution연산으로 입력 이미지의 특징을 추출한다. 연산과정을 살펴보자.
입력과 필터/커널의 원소값을 곱한 값을 모두 더한 값을 출력한다.

• Filter(kernel) 는 보통 3x3 or 5x5를 사용한다.
• 합성곱 연산의 결과를 특성맵 feature map이라고 한다.
• 위의 예시에서 필터의 크기는 3x3이고, 필터의 이동 범위 stride는 1이지만, 다르게 정할 수도 있다.
• 딥러닝 프레임워크에는 합성곱 convolution 연산 함수가 구현되어 있다.
  • python : conv_forward
  • tensorflow : tf.nn.conv2d
  • keras:conv2D

Vertical Edge Detection

합성곱 연산으로 어떻게 윤곽선/모서리(vertical edges, horizontal edges)를 감지할 수 있을까?

vertical edges 수직 윤곽선을 감지하는 사례를 convolutional operation 관점에서 살펴보자.

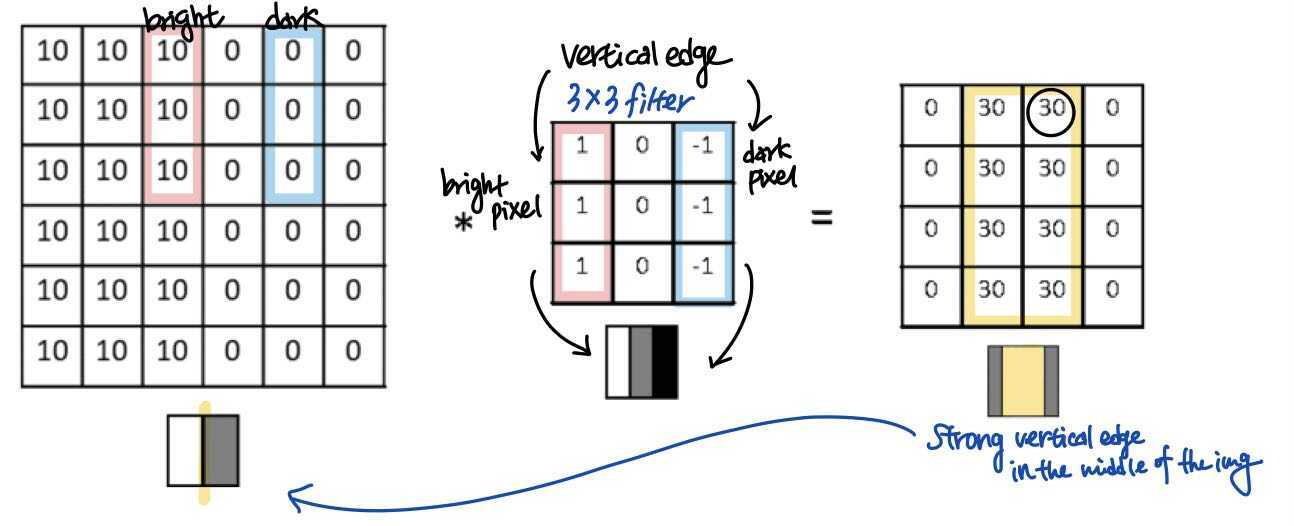
• 입력 이미지의 10과 0 사이의 경계선이 vertical edge 수직윤곽선이다.
• 3x3 필터를 통과해 합성곱 연산의 결과 특징맵은 밝은 부분이 중앙에 나타난다. 이는 입력 이미지의 경계선에 해당하는 부분이다.
• 예시에서 크기가 맞지 않고 감지된 경계선이 다소 두껍지만, input이미지가 작기 때문이다.

More Edge Detection

Vertical edge detection examples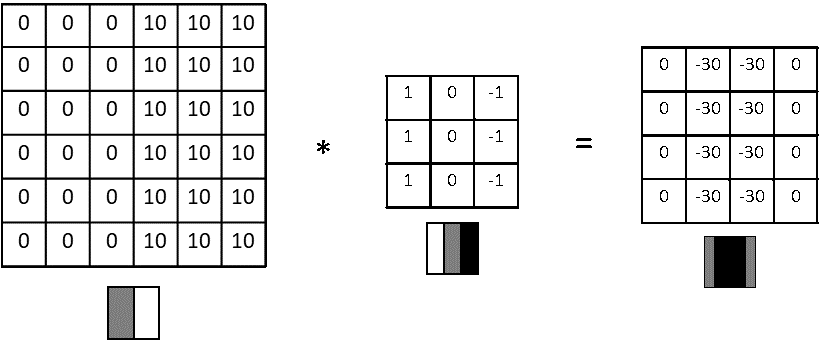

앞서 살펴본 예시와 반대인 케이스를 살펴보자.

• shade of the transitions is reversed : 30 > -30
  • 두 예시가 입력 이미지에서 차이가 있는 어두운 부분에서 밝은 부분으로 가는 것으로 바뀐 것이다.
  • 이러한 차이가 중요하지 않다면 결과 행렬에 절댓값을 씌워도 된다.

Vertical and Horizontal Edge Detection

세로, 가로 윤곽선을 검출해내는 필터는 다른 형태를 보인다.

Horizontal Edge

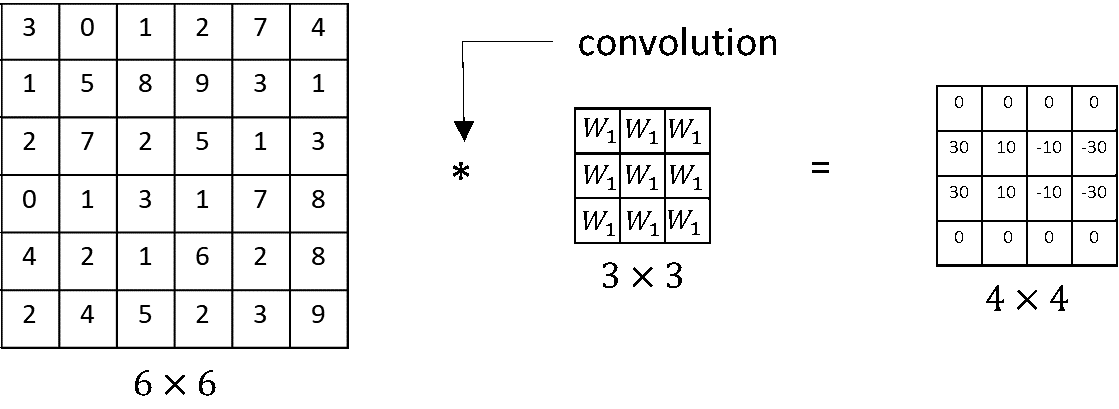
Horizontal Edge도 작은 이미지 예시를 보자.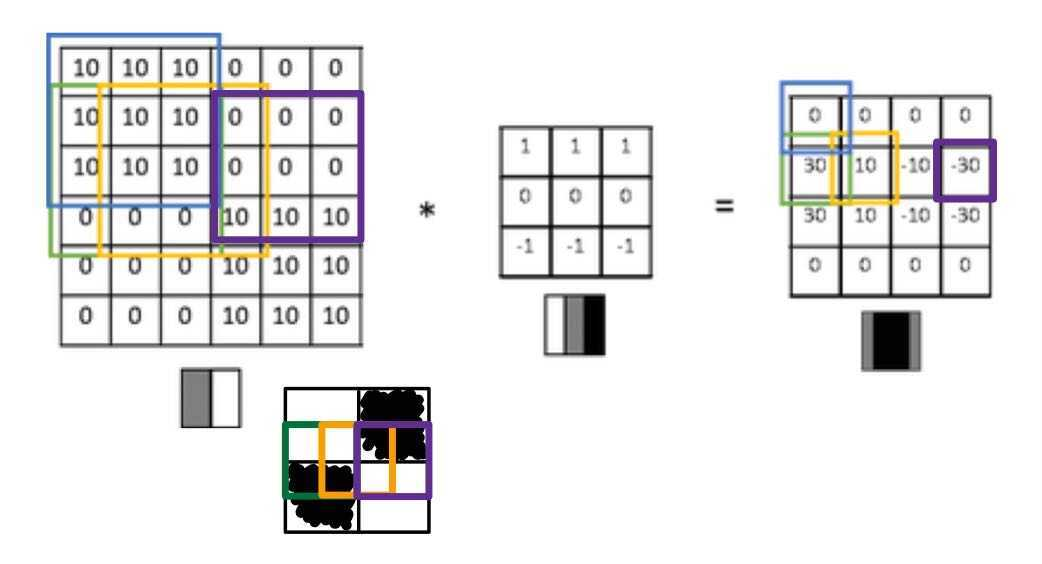

• 30 (green)이라는 숫자가 나온 것은 입력 이미지의 3x3영역이 확실히 위쪽이 밝은 픽셀, 아랫쪽이 어두운 픽셀이기 때문이다.
• -30 (purple)이라는 숫자는 30(green)과는 반대로 위쪽이 어두운 픽셀, 아랫쪽이 어두운 픽셀이기 때문이다.
• 10 (yellow)이라는 숫자가 나온 것은 필터가 그 부분의 왼쪽에 있는 positive edge(10)와 오른쪽에 있는 negative edge(0)을 인식해, 두가지가 섞여(blending) 중간 크기의 값 10이 나온 것이다.
  • 큰 이미지 데이터 (ex.1000 x 1000)에서는 이런 중간값은 상대적으로 작기 때문에 눈에 띄지 않는다.

Learning to detect edges

필터에 어떤 숫자 조합을 사용해야할까?!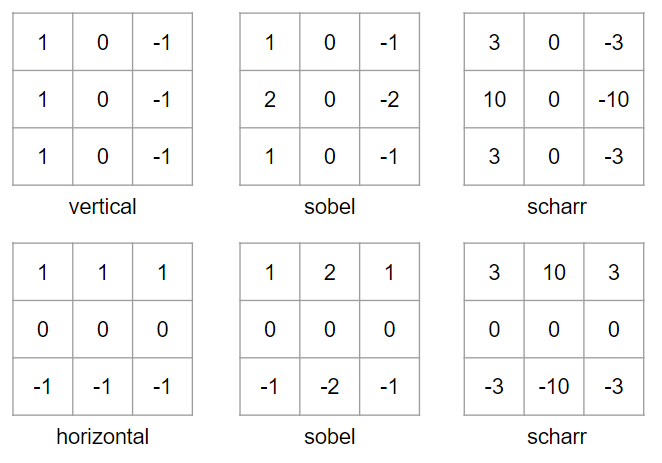

• Sobel filter : 중간 부분 픽셀에 중점을 둔다.
• Scharr filter

딥러닝에서는 복잡한 이미지의 윤곽선을 검출할 때 9개의 숫자를 직접 고를 필요없다. 이 숫자를 변수로 설정한 뒤, backpropagation을 사용해 학습된 3x3 filter의 숫자를 합성곱 연산으로 입력 이미지의 전체에 적용해 어떤 형태의 윤곽선도 검출할 수 있도록 할 것이다.

## Padding 앞서 살펴본 예시에서는 두가지 단점이 있다. - 반복해서 합성곱 연산을 하게되면 이미지가 축소된다. Convolution layer 여러개를 쌓았다면 최종 output은 input 보다 훨씬 작아지는 현상이 발생한다. - 가장자리 픽셀은 단 한번만 사용되어, 이미지 윤곽에 대한 정보 information near the border of the image를 버리게 된다.

단점을 해결하기 위해서 합성곱 연산을 하기 전에 이미지 주위에 추가로 하나의 경계를 덧대는 방법 패딩 Padding을 살펴보자. 일반적으로 값을 0으로 채우는 제로 패딩(zero padding) 을 사용하고, $p$=1인 경우는 다음과 같다.

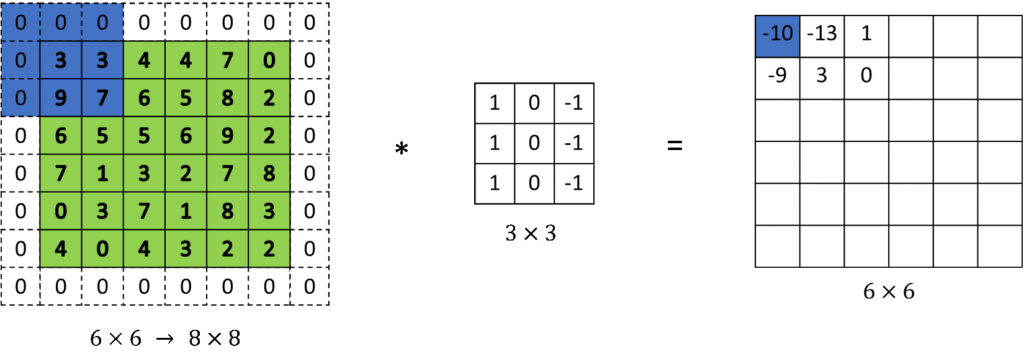
Valid and same convolutions

최종 이미지의 크기는 $(n + 2p - f + 1)$ x $(n + 2p - f + 1)$ 이다.
$n$ 이미지 크기, $p$ 패딩 크기, $f$ 필터 크기를 의미한다.

• Valid convolutions : no padding

  size of an input image	size of a filter	padding	size of an output image
  n×n	f×f	no padding, p=0	n−f+1×n−f+1
  6	3		6−3+1=4⇒4×4

• Same convolutions : pad so that output size is the same as the input size 패딩을 한 뒤 output 이미지의 크기가 input 이미지의 크기와 동일하다.

  size of an input image	size of a filter	padding	size of an output image
  n×n	f×f	p=1	n+2p−f+1×n+2p−f+1
  6	3		6+2−3+1=6⇒6×6

• 일반적으로 필터의 크기 $f$는 홀수이다.
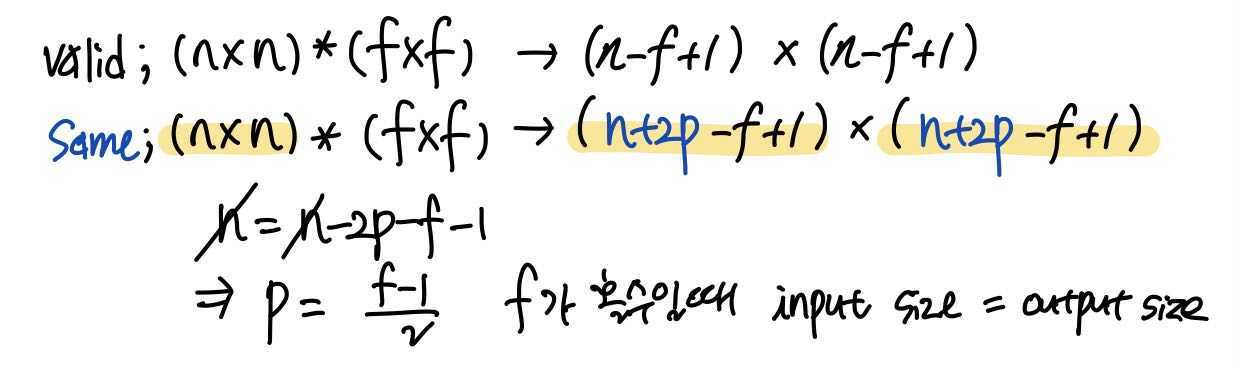
  • 짝수일 경우, 패딩이 비대칭이 되기 때문이다.
  • 홀수 크기의 필터(such as 3×3 or 5×5)는 central position 중심위치, 중심픽셀을 가지게 되는데, 이는 컴퓨터 비전에서 distinguisher로 용이하게 쓰인다.

Strided Convolutions

Stride

최종 이미지의 크기는 $⌊\frac{n–f+2p}{s}⌋+1$×$⌊\frac{n–f+2p}{s}⌋+1$ 이다.
$n$ 이미지 크기, $p$ 패딩 크기, $f$ 필터 크기, $s$ 스트라이드 크기를 의미한다.

Stride 스트라이드 $s$는 필터의 이동 횟수를 의미한다. 앞서 살펴본 예시에서는 필터가 한칸씩(stride=1) 이동해서 계산했지만, 스트라이드에 다른 수를 지정하면 그 수만큼 필터가 이동해서 계산한다.

7×7 input image & 3×3 filter with a stride of 2 의 예시를 보자.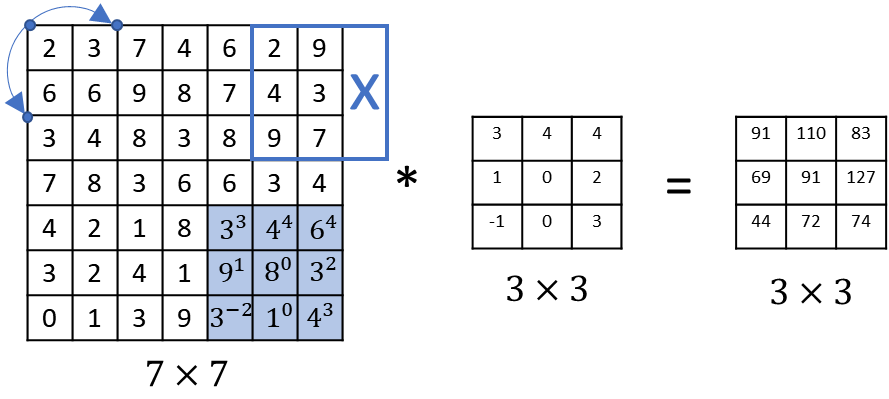

size of an input image	size of a filter	padding	stride	size of an output
n×n	f×f	p	s	$⌊\frac{n–f+2p}{s}⌋$+1×⌊$\frac{n–f+2p}{s}⌋$+1
7	3	0	2	(7-3+0)/2+1 ⇒3×3

• 이때, $\frac{n–f+2p}{s}$ 분수가 정수가 아닐 경우 내림값을 구한다. (⌊$z$⌋ = floor($z$) 내림을 의미)

• 보통은 필터가 패딩을 더한 input 이미지에 맞게 (크기가 정수가 될 수 있도록) 패딩과 스트라이드 수치를 설정 후, 결과를 계산한다.

• p=1, strides =2 연산과정

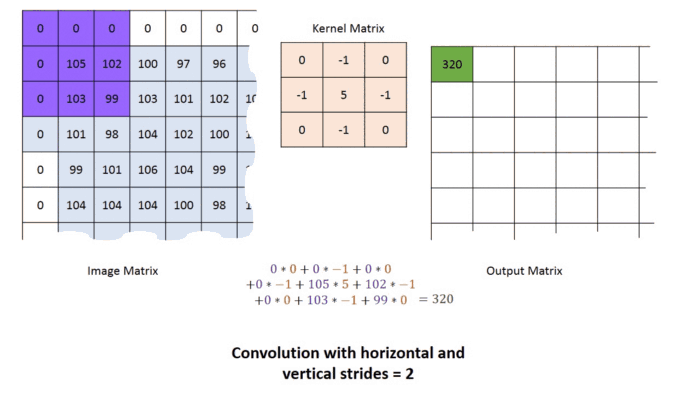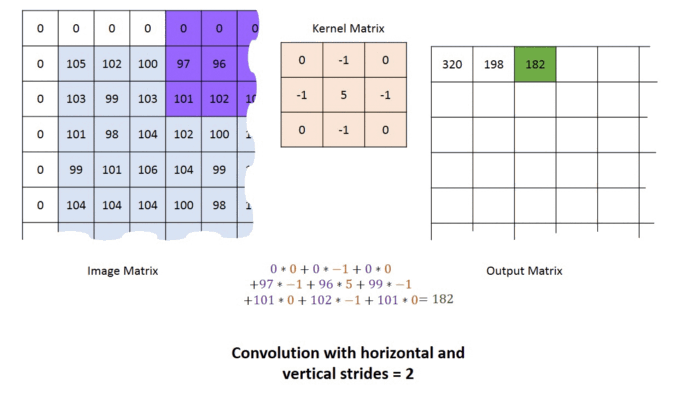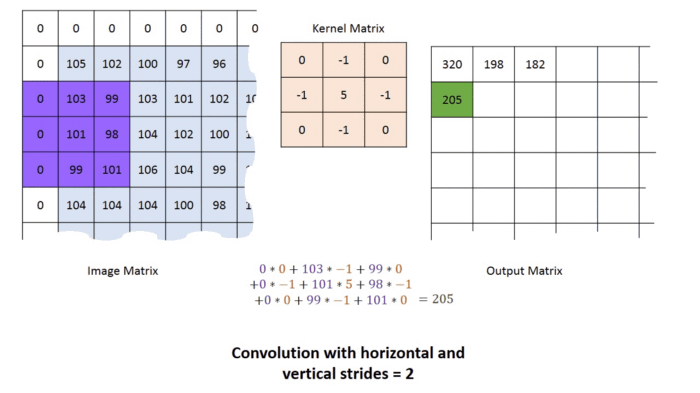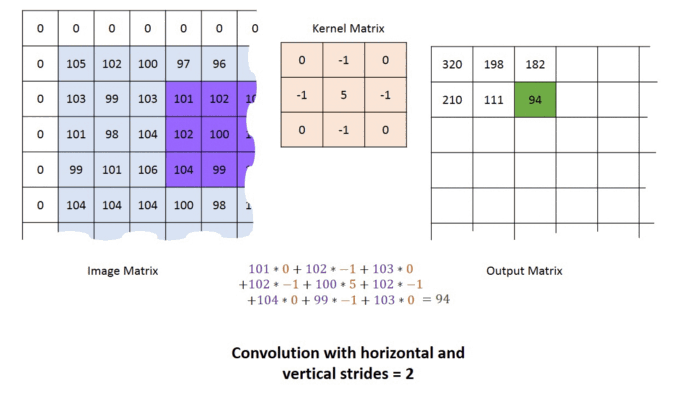
Tehnical note on cross-correlation vs. convolution

우리가 배운 합성곱은 사실 교차상관cross-correlation 이지만 딥러닝에서는 관습적으로 합성곱이라고 부른다. 일반적 수학적 정의와 어떤 차이가 있는 지 확인해보자.

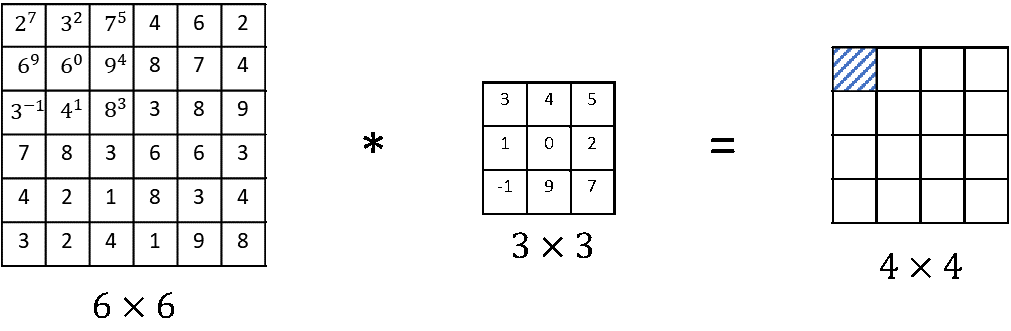
• 일반적으로 수학에서 정의하는 합성곱은 요소들을 곱하고 더하는 과정(합성곱 연산) 전에 필터를 가로축과 세로축으로 뒤집는 연산을 해준다. flipping computation: flipping vertically and horizontally 가로축과 세로축으로 필터를 아래 이미지처럼 뒤집은 뒤, 우리가 아는 합성곱 연산을 수행한다.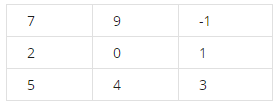
  수학의 특정분야, 신호처리 분야에서는 flipping연산을 하는 것이 합성곱 연산이 특수한 성질인 결합법칙 associativity (A*B)*C=A*(B*C)를 가지게해 유용하다.

• 그러나, 딥러닝에서는 뒤집는 연산을 생략하고, convolution이라고 부른다. 이 뒤집는 과정은 신호처리에서는 유용하지만 심층 신경망 분야에서는 아무런 영향이 없기 때문이다.

Convolutions Over Volume

Convolutions on RGB images

이미지에 색상(RGB)이 들어가면 입체형으로 변하게 되고, 차원이 하나 증가해 (높이 x 넓이 x 채널) 형태가 된다. 여기서 채널channel은 색상 또는 입체형 이미지의 깊이를 뜻한다. 이에 따라 합성곱에 사용되는 하나의 필터도 각 채널 별로 하나씩 증가하게 된다.

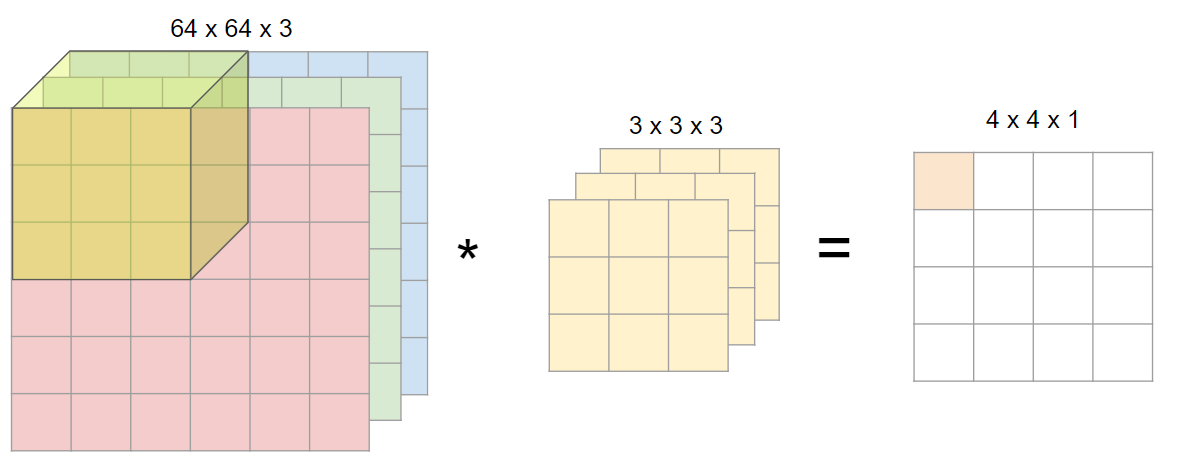
• 입력 데이터의 채널 수 = 필터의 채널 수
  • 다수의 채널을 가진 입력 데이터로 합성곱 연산을 하는 경우, 필터의 채널 수도 입력의 채널 수만큼 존재해야한다.
    • 예시에서 input image (64x64x3) filter (3x3x3) 채널 수가 동일하다.
  • 각 채널 별로 필터는 모두 같은 것을 사용할 수도 있고 다른 것을 사용할 수도 있다. (하기 이미지 예시 참고)
• 모든 채널의 합성곱 연산을 더해 최종 output 특성 맵을 출력한다.
  

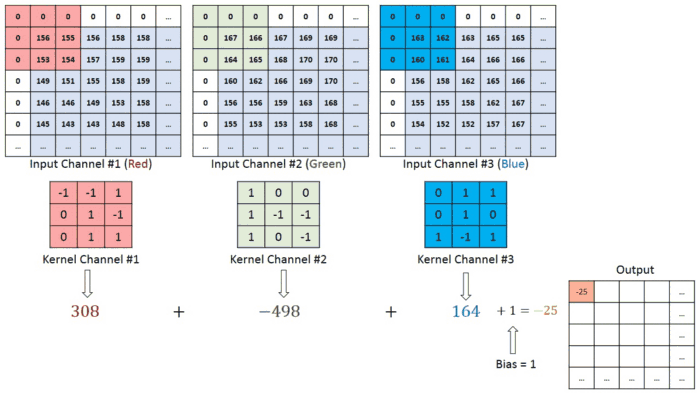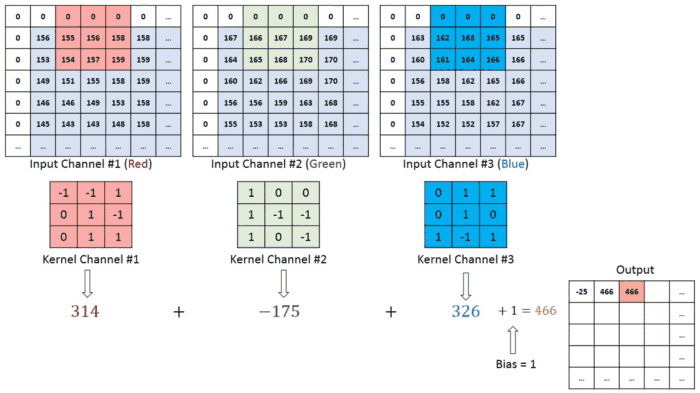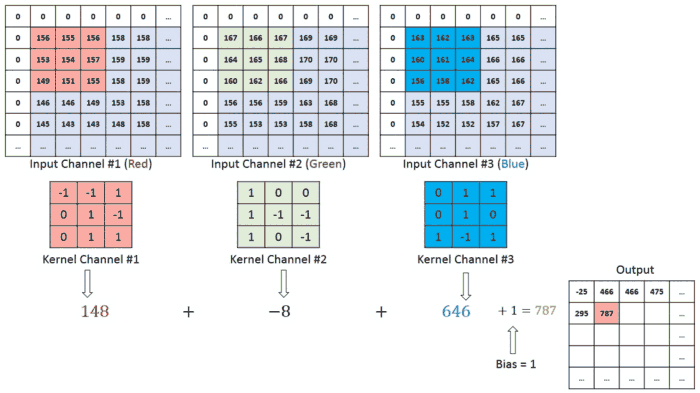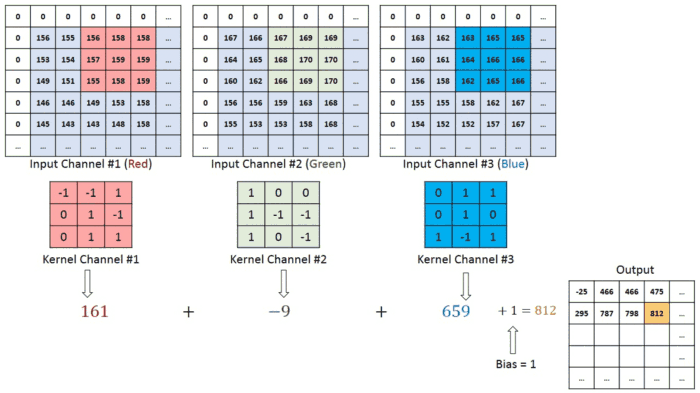
Multiple filters

여러 개의 윤곽선을 감지하려면, 여러개의 필터를 동시에 사용하게 된다. what if we want to use multiple filters at the same time?
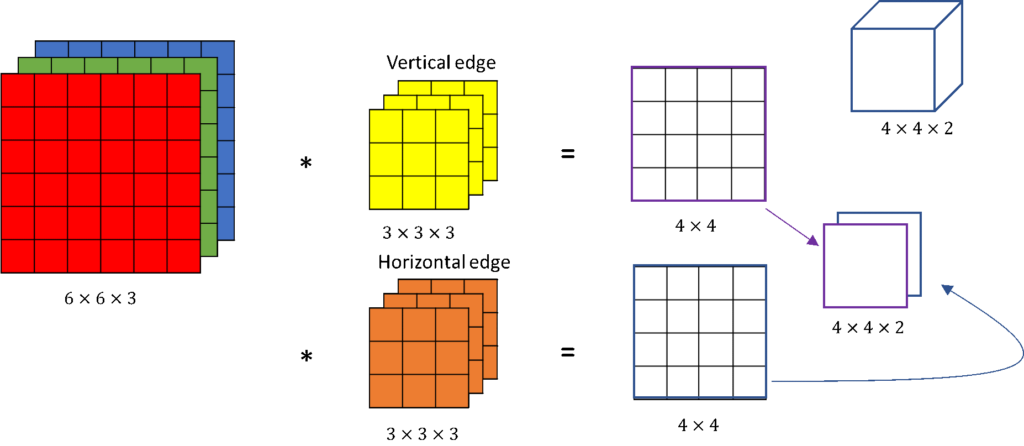위와 같이 두개의 필터를 사용한다고 가정해보자. 입력 이미지와 2개의 filter 각각 convolution 연산을 통해 2개의 얻은 2개의 4×4 outputs 쌓아 4×4×2 output volume을 얻는다. output volume은 다수의 필터를 사용했음을 의미하고, 4×4×2 volume 박스형태로 그리기도 한다. 해당 예시에서 10개의 필터를 사용했을 경우, output volume은 4x4x10이 된다.

Convolution on volumes
$(n×n×n_c)*(f×f×n_c) = (n−f+1)×(n−f+1)×n_c′$
*$n$ 이미지크기, $n_c$ 채널 수, $f$필터크기, $n_c′$ 사용된 필터 수

One Layer of a Convolution Network

Example of layer

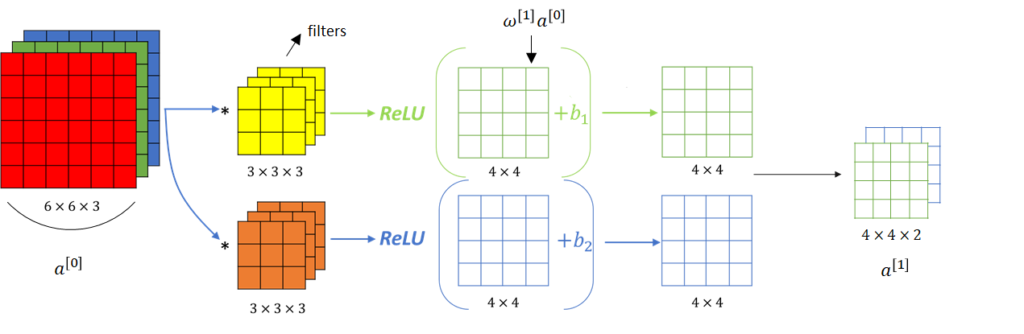Convolution Network with two filters 의 한 레이어를 나타낸 것이다.

1. Input
   $a^{[0]}=x$
2. 합성곱 연산 (linear Operation) → 편향 추가
   $Z^{[1]}=W^{[1]}×a^{[0]}+b^{[1]}$,
3. 비선형 활성화 함수 (usually ReLU)
   $a^{[1]}=g(Z^{[l]})$
   $a^{[1]}$은 다음 레이어의 입력값이 된다.

Number of parameters in one layer

• Let’s suppose we have 10 filters that are 3×3×3 in one layer of a neural network. So, how many parameters does this layer have?
  
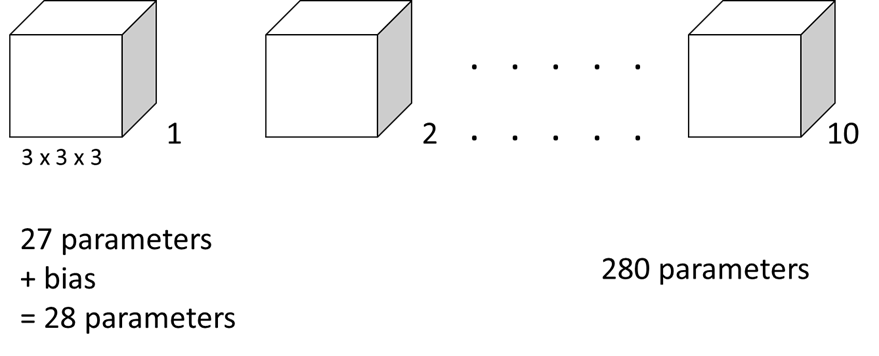
  • 3×3×3 필터 하나는 27개의 parameters 와 편향 bias 까지 총 28개의 parameters가 있고, 이러한 필터가 10개이므로 해당 레이어에 총 280개의 parameters가 존재한다.
  • input image가 아무리 커지더라도 (1000×1000 or 5000×5000..) parameters의 수가 280개로 고정되어 이 10개의 필터(feature detector)만으로도 다른 특징들을 검출해낼 수 있다는 장점이 있다. even in the very large image with just a very small number of parameters CNN의 이러한 특징은 과적합을 방지한다.

📍Summary of ConvNet

• Notation
  • $l$ : $l$ 번째 계층
  • $f^{[l]}$ : 필터의 크기
  • $p^{[l]}$ : 패딩의 양
  • $s^{[l]}$ : 스트라이드 크기
  • $n_H$ : 이미지의 높이
  • $n_W$ :이미지의 넓이
  • $n_c$ : 채널의 수
  • $n_c′$ : 필터의 수
    
    
• Application
  • 다음 연산이 $l$ 번째 층의 연산이면,
    이전 층 $(l−1)$ 의 이미지의 크기 : $n_H^{[l-1]} \times n_W^{[l-1]} \times n_c^{[l-1]}$
    그 결과로 나오는 이미지의 크기 : $n_H^{[l]} \times n_W^{[l]} \times n_c^{[l]}$
  • $l$ 번째 층의 높이 혹은 넓이의 크기연산 공식
    $n_H^{[l]} = \displaystyle \frac{n_H^{[l-1]} + 2p^{[l]} - f^{[l]}}{s^{[l]}} + 1$
    $n_W^{[l]} = \displaystyle \frac{n_W^{[l-1]} + 2p^{[l]} - f^{[l]}}{s^{[l]}} + 1$
    
    
• Computation
  1. $n_c^{[l]}$개의 크기가 $f^{[l]} \times f^{[l]} \times n_c^{[l-1]}$인 필터가 합성곱 연산을 진행
  2. 활성화 함수를 거쳐 $l$ 번째 층의 결과값 계산
  3. 합성곱 연산에 사용된 변수는 총 $f^{[l]} \times f^{[l]} \times n_c^{[l-1]} \times n_c^{[l]}$ 개, 추가된 편향까지 더하면 한 층의 합성곱 신경망에 필요한 변수는 $f^{[l]} \times f^{[l]} \times n_c^{[l-1]} \times n_c^{[l]} + n_c^{[l]}$개
  • 기존의 단순 신경망의 가중치행렬 $W^{[l]}$의 크기 $(n_H^{[l-1]} \times n_W^{[l-1]} \times n_c^{[l-1]}) \times (n_H^{[l]} \times n_W^{[l]} \times n_c^{[l]})$ 인데, 이보다 더 적은 변수로 계산이 가능해 진 것이다.
    
    
• EX) 28 x 28 x 3 이미지, 동일한 5 x 5 필터 20개, 패딩없고 스트라이드는 1 → 24 x 24 x 20 크기의 output
  • 합성곱 연산에 필요한 총 변수의 크기는 5 x 5 x 3 x 20 + 20(bias) = 1520 이다. 반면, 단순 신경망을 사용하여 같은 크기의 결과를 나타내려면 (28 x 28 x 3) x (24 x 24 x 20) + (24 x 24 x 20) = 27,106,560 만큼의 변수가 필요하다.

Simple Convolutions Network Example

ConvNet

valid convolution예를 통해서 앞서 학습한 공식, notation을 적용해보자.

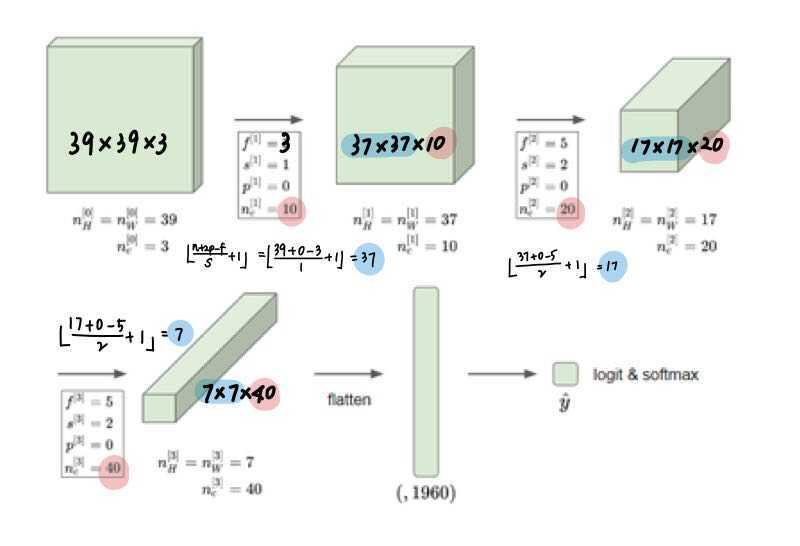
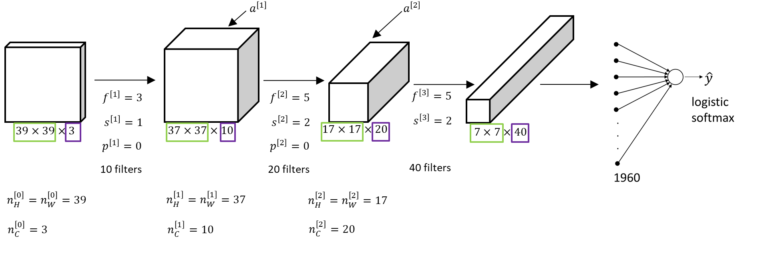
• 합성곱 신경망의 크기는 깊어질 수록 점점 줄어든다.

Types of layer in a convolutional network

• Convolution(conv)
• Pooling(pool)
• Fullyconnected(FC)

Pooling Layers

Pooling Layer는 convolution layer의 출력 데이터를 입력으로 받아 풀링연산을 통해 출력 데이터(Activation map)의 크기를 줄여 연산 속도를 높이고, 특징을 더 잘 검출할 수 있게 한다.(특정데이터를 더 강조)

일반적으로 ConvNet에서는 Convolution layer (합성곱 연산 + 활성화 함수) 다음에 Pooling layer를 추가한다.

📍 Pooling layer Operation

• $n=4, f=2, p=0, s=2$
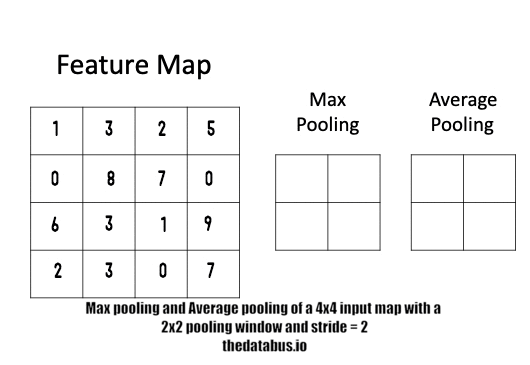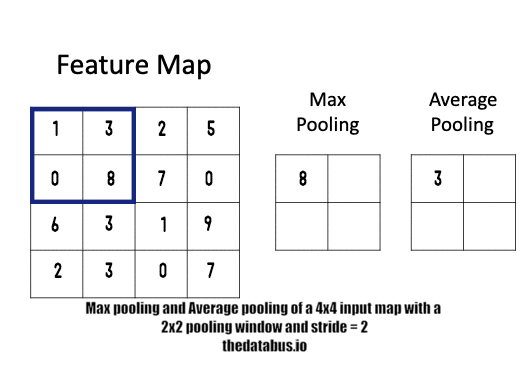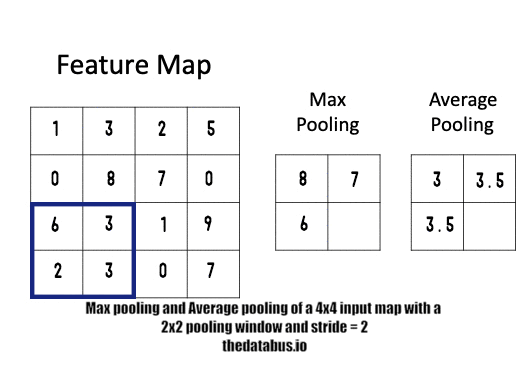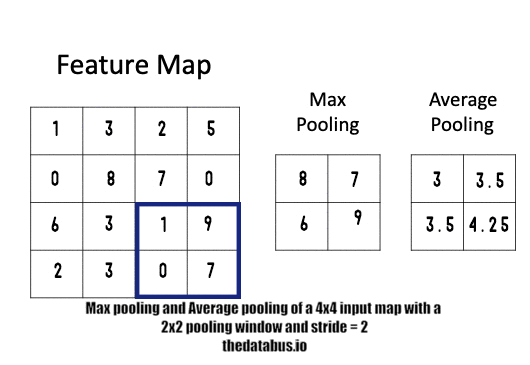
• $n_H$ x $n_w$ x $n_c$ ⇒ pooling layer ⇒ ⌊$n_H -f \over s$+1⌋ x ⌊$n_W -f \over s$+1⌋ x $n_c$

size of an input image	filter size	stride	padding	type of pooling	size of an output image
$n_H$ x $n_w$x $n_c$	f×f	s	p=0 (rarely used)	Maxpooling or Averedge pooling	⌊$n_H -f \over s$+1⌋ x ⌊$n_W -f \over s$+1⌋ x $n_c$

Max pooling
정사각 행렬의 특정 영역 안에 값의 최댓값을 모으는 방식으로 동작한다. max pooling에서는 패딩을 잘 사용하지 않는다 p=0. (한가지 예외는 존재)

Average pooling
정사각 행렬의 특정 영역의 평균을 구하는 방식으로 동작한다.

Summary of pooling

• 학습할 parameter는 없고 Hyperparameter($f$,$s$, Max or average pooling)만 존재하기 때문에 fixed computation이다.(경사하강법, 역전파를 적용할 변수가 존재하지 않는다.)
  • $f=2, s=2$ OR $f=3, s=2$ 자주 사용
  • CNN에서는 주로 Max pooling을 사용한다.
    • 한가지 예외 존재 ( 심층 신경망 7x7x1000 > 1x1x1000 )
      $n_H$ x $n_w$ x $n_c$ ⇒ ⌊$n_H -f \over s$+1⌋ x ⌊$n_W -f \over s$+1⌋ x $n_c$
  • pooling layer를 지나면 행렬의 크기가 감소한다.
    shrinking the height and width
  • pooling layer를 지나더라도 채널 수($n_c$)는 변경되지 않는다.
    • pooling은 각 채널에 개별적으로 적용되기 때문이다.

CNN Example

Neural Netwrok example

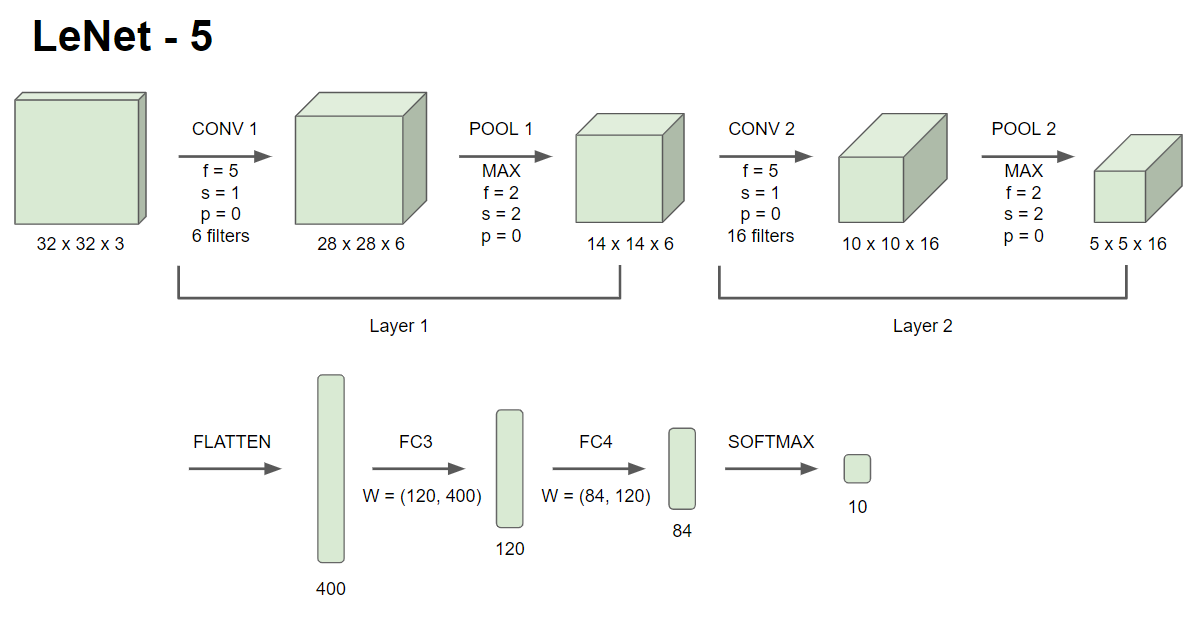
• 일반적인 구조 예시
  • Layer 1 (CONV1+POOL1), Layer 2 (CONV2+POOL2)
    • 신경망의 층의 갯수를 말할 때, 학습시킬 가중치나 모수가 있는 층layer만 카운트한다. 이는 위의 이미지에서 CONV1 과 POOL1을 각각의 layer로 보지 않고 하나의 층인 layer1으로 부르는 이유이다. (앞서 살펴봤듯이 Pooling layer는 모수가 없고 fixed hyperparameter만 존재한다.)
  • FLATTTEN
  • FC3, FC4 단일 신경망과 유사하다.
  • Softmax Unit

• common pattern in CNN
  • 신경망이 깊어질수록 크기 $n_H, n_W$는 점점 줄어든다.
  • 반면 채널 수는 증가한다.
  • One or more conv layers followed by a poolinglayer, and then one or more conv layers followed by a pooling layer. At the end we can have a few Fullyconnected layers being followed by a softmax function (or sigmoid for binary classification problem). This is pretty common pattern that we see in convolutional neural networks.

• dimensions of particular volumes and the number of parameters

  	Activatonshape	Actiovationsize	# of parmeters
  Input	(32×32×3)	3027	0
  Conv1 (f=5,s=1)	(28×28×3)	6272	208
  Pool1	(14×14×8)	1568	0
  Conv2 (f=5,s=1)	(10×10×16)	1600	426
  Pool2	(5×5×16)	400	0
  FC3	(120×1)	120	48001
  FC4	(84×1)	84	10081
  softmax	(10×1)	10	841

  • Pooling layer는 모수가 없다.
  • Conv layer는 상대적으로 적은 수의 파라미터를 가진다.
  • FC layer는 많은 파라미터를 가진다.
  • 활성값의 크기Activation size도 신경망이 깊어질 수록 점차 감소한다. 너무 빠르게 감소한다면, 성능이 안좋을 수 있다.

Why Convolutions?

완전 연결 층 FC 대신 합성곱층 Conv를 사용할 때 2가지 이점 : parameter sharing, sparsity of connections

Advantages of Convnet

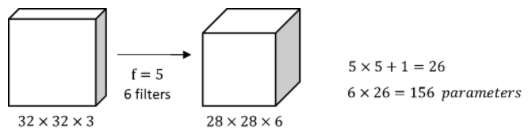(32×32×3)차원의 입력 이미지는 (5×5×3) 크기의 filter 6개와 합성곱 연산을 통해 (28×28×6)차원의 결과값을 얻는다. 이 때 연산에서 필요한 파라미터는 ((5×5×3)+1)X6 = 456개이다.
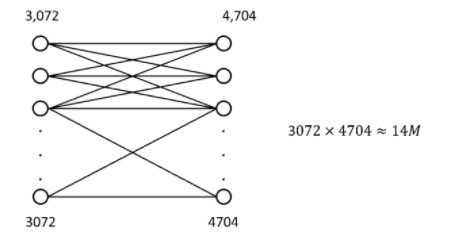(32×32×3) → 3,072개의 유닛을 하나의 레이어에 두고 (28×28×6) → 4,704 유닛들을 다음 레이어에 둔 뒤 각각 뉴런들을 모두 연결Fully Connected하면 3072 x 4704 약 14만개의 파라미터가 필요하다. 입력이미지가 작음에도 불구하고 변수가 많이 필요하고, 입력값이 커질수록 가중치 행렬이 연산 불가능할 정도로 커진다.

합성곱신경망이 이렇게 적은 변수를 필요로하는 이유를 살펴보자.

• parameter sharing 변수공유
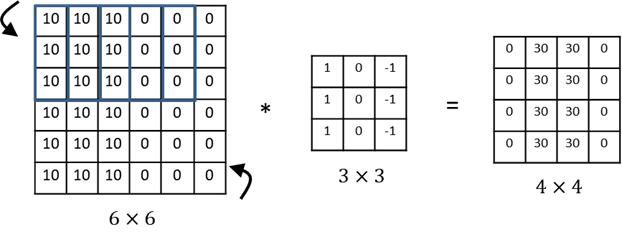  feature detector 속성 검출기 vertical edge detector 세로 윤곽선 검출을 위해 (3x3) 필터 를 사용한다고 생각해보자. 이 필터는 윤곽선 혹은 다른 특성들을 검출하기 위해 입력 이미지의 여러 위치에서 동일하게 사용될 수 있다. 9개의 변수를 공유하며 16개의 출력을 계산하는 것은 변수의 개수를 줄이는 방법 중 하나이다. 이는 윤곽선과 같은 하급 속성뿐만 아니라
  눈, 고양이와같은 상급 속성을 인식하는데도 적용이 된다.

• sparsity of connections 희소연결
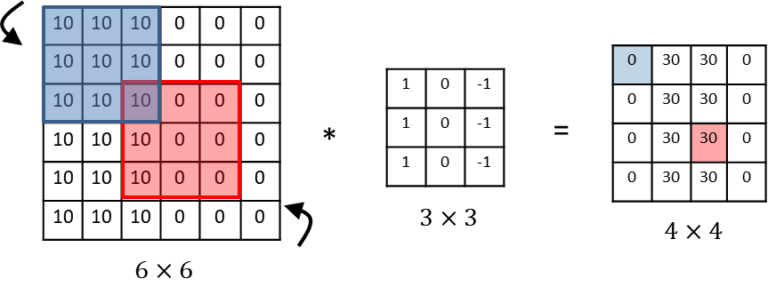  결과값의 파란 부분은 입력 값의 파란 부분에만 영향을 받는다. (합성곱연산과정) 빨간 부분도 마찬가지이다. 이렇듯 출력값이 이미지의 일부(작은 입력값)에 영향을 받고, 나머지 픽셀들의 영향을 받지 않는 것이다.

합성곱 신경망의 변수공유와 희소연결이라는 특징때문에 신경망 변수가 줄어들어 작은 훈련 세트를 가지게하고, 과대적합도 방지할 수 있다 .

• Translation invariance 이동불변성
  합성곱 신경망은 이동 불변성을 포착하는데도 용이하다. 합니다. 몇 픽셀 이동한 이미지(an image shifted a few pixels)도 유사한 속성을 가지게 되고, 입력 이미지의 모든 위치에 동일한 필터를 적용해 신경망이 자동적으로 학습하고 이동불변성을 포착할 수 있다. 즉, 이미지가 약간의 변형이 있어도 이를 포착할 수 있다는 것이다.

Putting it together!

Car detector 예제로 전체적인 흐름을 보자.

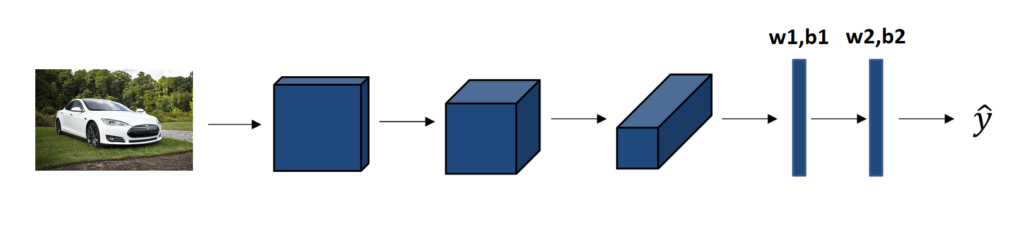
• x image
• y binary label(or K-classes)
• convolutional neural network structure
  • Some convolutional and Poolinglayers.
  • Fullyconnected layers followed by a softmax output
• Parameters & CostFunction
  • Conv, FC : parameters w, biases b
  • Cost function J : 신경망 훈련세트에 대한 예측의 손실losses 합을 m으로 나눈 것
• Training : gradient descent or some other optimization algorithm(gradient descent with momentum) to reduce J.

---

Source and Reference
cs231n | CNN More On Edge Detection | datadriveninvestor | towardsdatascience