
1. 큐의 이해와 ADT 정의
큐는 앞서 설명한 스택과 함께 언급되고 또 비교되는 자료구조이다.
스택은 먼저 들어간 데이터가 나중에 나오는 구조인 반면, 큐는 먼저 들어간 데이터가 먼저 나오는 구조이다.
이것이 스택과 큐의 유일한 차이점이다.
앞 챕터에서 스택의 이해를 돕기 위해 쟁반과 접시를 예로 들었다.
하지만 큐의 이해를 위해서 별도의 예를 들 필요는 없다.
큐는 우리에게 매우 익숙한 자료구조이기 때문이다.
우리는 하루에도 몇 번씩 줄을 선다.
줄을 서는 이유는 먼저 온 사람이 먼저 서비스를 받도록 하기 위함이다.
이렇듯 큐는 '선입선출' 구조의 자료구조이다.
때문에 'FIFO(First-In, First-Out) 구조의 자료구조'라 불린다.
스택과 마찬가지로 큐의 ADT도 정형화 된 편이다.
그럼 큐의 핵심이라 할 수 있는 두 가지 연산을 소개하겠다.
- enqueue: 큐에 데이터를 넣는 연산
- dequeue: 큐에서 데이터를 꺼내는 연산스택에서 데이터를 넣고 빼는 연산을 가리켜 각각 push, pop이라 하는 것처럼, 큐에서 데이터를 넣고 빼는 연산에 대해서도 각각 enqueue, dequeue라는 별도의 이름을 붙여주고 있다.
그럼 이어서 큐의 ADT를 제시하겠다.
물론 이것이 큐의 보편적인 ADT이다.

그럼 이제 큐를 구현해볼 텐데, 큐 역시 스택과 마찬가지로 배열을 기반으로, 그리고 연결 리스트를 기반으로 구현이 가능하다.
따라서 이번에도 배열 기반의 큐와 연결 리스트 기반의 큐를 각각 구현해볼 것이다.
2. 큐의 배열 기반 구현
배열 기반의 큐를 구현하기에 앞서 먼저 그 구조를 고민해야 한다.
큐는 스택과 큰 차이를 보이지 않지만, 스택과 달리 고민할 것이 몇 가지 더 있기 때문이다.
다음 그림에서는 길이가 4인 배열 대상의 enqueue 연산을 보이는데, 그림에서 F는 Front의 약자로 큐의 머리를, R은 Rear의 약자로 큐의 꼬리를 가리키는 일종의 변수를 의미한다.
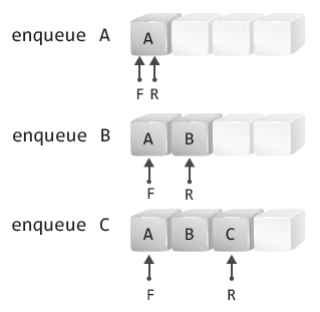
위 그림에서 F가 가리키는 것이 큐의 머리이고, R이 가리키는 것이 큐의 꼬리이다.
따라서 enqueue 연산 시 R이 그 다음 칸을 가리키게 되고, 그 자리에 새 데이터가 저장된다.
그렇다면 dequeue 연산 시에는 어떠한 데이터를 반환하고 소멸해야 하겠는가?
F가 가리키는 데이터가 저장순서가 가장 앞선 데이터이므로 F가 가리키는 데이터를 대상으로 dequeue 연산을 진행해야 한다.
즉 F를 참조하여 dequeue 연산을 하고, R을 참조하여 enqueue 연산을 한다.
따라서 큐는, 우아한 표현은 아니지만 '뒤로 넣고 앞으로 빼는 자료구조'라고도 한다.
자! 그럼 위 그림의 마지막 상태에서 dequeue 연산을 진행해 보겠다.
dequeue 연산의 예는 다음과 같다.
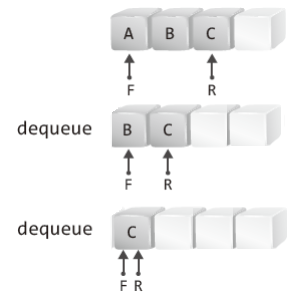
위 그림에서 보이는 방식은, dequeue 연산 시 반환할 데이터를 배열의 맨 앞부분에 위치시키는 방식으로 가장 보편적으로 인식하는 배열의 삭제방법을 적용한 것이다.
사실 이 방법을 적용하면 dequeue 연산의 대상이 맨 앞부분에 위치하므로, 그림에서 보인 것과 달리 F가 불필요하다.
하지만 이 방식은 dequeue 연산 시마다 저장된 데이터를 한 칸씩 이동시켜야 하는 단점이 있다.
때문에 배열 기반의 큐에서는 위의 방식으로 dequeue 연산을 진행하지 않는다.
그럼 실제로 적용하는 dequeue 연산의 방법을 소개하겠다.
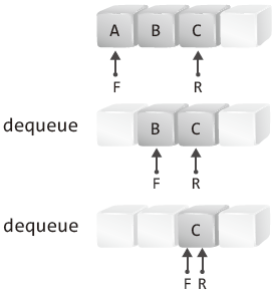
위 그림에서는 dequeue 연산 시 F를 이동시키고 있다.
이 방식을 취하게 되면 dequeue의 과정에서 데이터의 이동이 필요치 않다.
그저 F가 가리키는 위치만 한 칸 오른쪽으로 옮기면 그뿐이다.
하지만 이 방법도 완전하지는 않다.
다음과 같은 경우가 발생하기 때문이다.

위의 그림은 문자 D가 배열의 끝에 저장된 상황이다.
때문에 더 이상 R을 오른쪽으로 이동시킬 수 없다.
그런데 dequeue 연산도 몇 차례 진행이 되어 배열의 앞부분은 비어있다.
이 상황에서 우리는 어떻게 추가로 enqueue 연산을 진행해야 할까?
"R을 배열의 앞부분으로 이동시키면 되잖아요!"
"그럼 추가로 enqueue 연산을 진행할 수 있을 것 같은데요."정답이다! 쉽게 말해서 R을 회전시키는 것이다.
R이 배열의 끝에 도착하면, 다시 맨 앞으로 이동시켜서 R이 회전하게 만드는 것이다.
물론 R을 뒤쫓아 가는 F도 배열의 끝에 도달하면 회전해야 한다.
그리고 이러한 방식으로 동작하는 배열 기반의 큐를 가리켜 '원형 큐(circular queue)'라 한다.
논리적으로 배열이 원형의 형태를 갖춘다고 해서 붙여진 이름이다.
앞서 우리는 R과 F를 회전시켜서, 큐를 구성하는 배열을 효율적으로 사용하자는 결론에 도달했다.
그런데 R과 F를 회전시킨다는 것은 배열을 다음의 형태로 바라본다는 뜻이 된다.
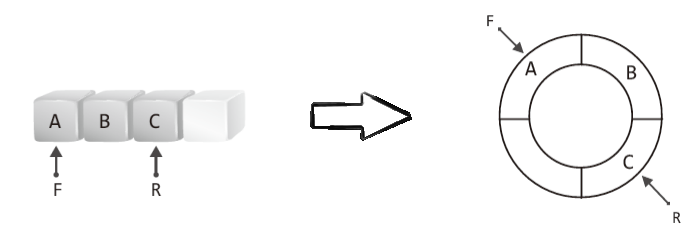
때문에 우리는 실제로 원형 큐를 구현하기 전까지, 원형 큐를 논리적으로 위 그림의 형태로 바라보기로 하겠다.
원형 큐도 앞서 보인 큐와 마찬가지로 첫 번째 데이터가 추가되는 순간 F와 R이 동시에 그 데이터를 가리킨다.
그 녀석이 큐의 머리이지 꼬리이기 때문이다.
따라서 위의 그림은 다음의 과정을 거쳐서 완성된 것이다.
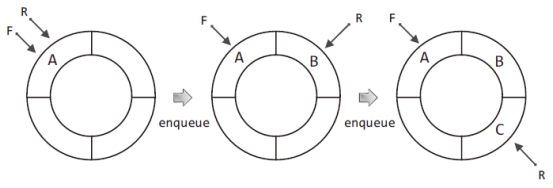
그리고 위의 그림을 대상으로 총 2회에 걸쳐서 dequeue 연산을 진행하면, 다음의 상태에 이르게 된다.
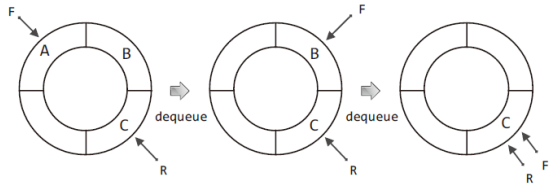
그럼 이제 구현만 하면 될까? 아니다!
위의 모델에서도 생각해볼 문제가 있다.
이의 확인을 위해서 먼저 위의 enqueue 연산 과정의 그림에서 문자 D를 추가해보자.
그리고 dequeue 연산 과정의 그림에서도 한 차례 더 dequeue 연산을 진행해 보자.
즉 큐를 완전히 채워보고 또 완전히 비워보자는 뜻이다.
그럼 다음 그림을 통해서 그 결과를 확인하자.
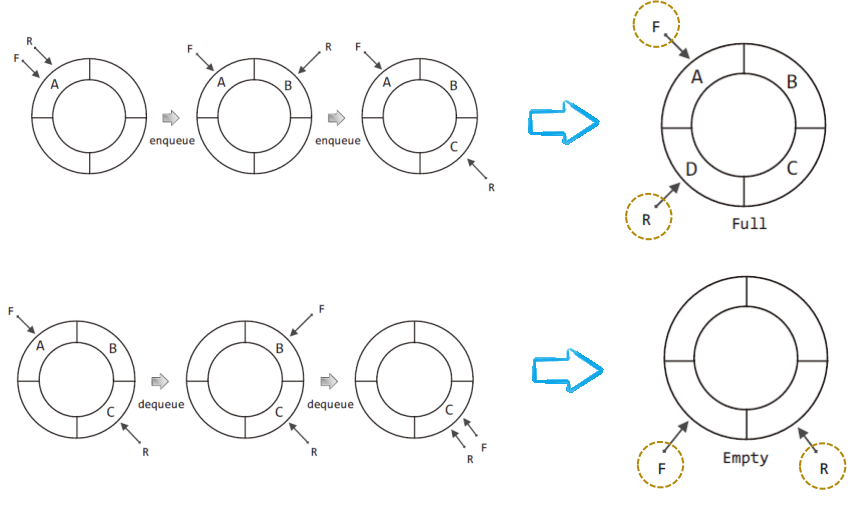
위 그림을 보면, 큐가 꽉 찬 경우나 텅 빈 경우나 F가 R보다 한 칸 앞 선 위치를 가리킴을 알 수 있다.
그리고 이것이 의미하는 바는 다음과 같다.
"F와 R의 위치만 가지고는 꽉찬 경우와 텅 빈 경우를 구분할 수가 없다!"그럼 이에 대한 해결책은 무엇일까?
"배열을 꽉 채우지 않는다!"
"꽉 차면 구분이 안되니 꽉 채우지 않는 것이다!"조금 허술한 해결책 같지만 아주 멋진 해결책이다.
그리고 이것이 의미하는 바는 다음과 같다.
"배열의 길이가 N이라면 데이터가 N-1개 채워졌을 때, 이를 꽉 찬 것으로 간주한다!"이렇게 하면 저장 공간 하나를 낭비하게 된다.
하지만 이로 인해서 문제 하나가 해결이 되는 셈이니 잃는 것보다 얻는 것이 더 많다.
그리고 혹시나 해서 말하지만, F와 R의 위치는 계속 회전한다.
따라서 F와 R의 상대적 위치 차를 통해서 텅 빈 경우와 꽉 찬 경우를 구분해야 한다.
그럼 이러한 결론을 반영해서 큐가 채워지는 과정을 다시 한 번 정리해 보겠다.
다음 그림에서는 큐가 처음 생성되어 텅 빈 경우를 보이고 있다.
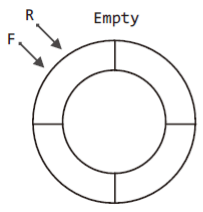
위 그림에서는 F와 R이 같은 위치를 가리키고 있다.
이전에는 첫 번째 데이터가 저장된 경우, 이 데이터가 머리이자 꼬리이기 때문에 F와 R이 같은 위치를 가리키게 하였다.
하지만 지금은 공간 하나를 비우기로 하였으니, F와 R이 같은 위치를 가리키는 이 상태가 텅 빈 상황을 표현한 것이 된다.
그럼 이 상황에서 계속해서 데이터를 채워보겠다.
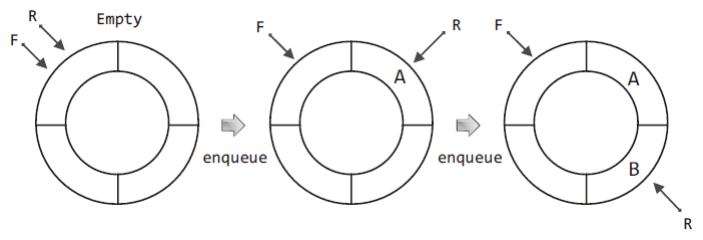
위 그림을 통해서 다음 두 가지 사실을 정리할 수 있다.
이는 실제 큐의 구현을 위해서 인지하고 있어야 하는 내용들이다.
"enqueue 연산 시, R이 가리키는 위치를 한 칸 이동시킨 다음에, R이 가리키는 위치에 데이터를 저장한다.""dequeue 연산 시, F가 가리키는 위치를 한 칸 이동시킨 다음에, F가 가리키는 위치에 저장된 데이터를 반환 및 소멸한다."이 중에서 특히 dequeue 연산 시에도 F가 가리키는 위치를 우선 한 칸 이동한다는 사실을 잊지 말자.
그리고 비록 dequeue 연산의 결과를 그림으로 보이지는 않았지만, 위 그림을 통해서 충분히 예상할 수 있을 것이다.
그럼 마지막으로 한 번 더 enqueue 연산을 진행해서 큐를 꽉 채워보겠다.
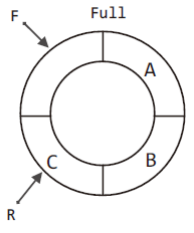
이로써 우리가 구현할 큐의 특성 두 가지를 다음과 같이 추가로 정리할 수 있다.
- 원형 큐가 텅 빈 상태: F와 R이 동일한 위치를 가리킨다.
- 원형 큐가 꽉 찬 상태: R이 가리키는 위치의 한 칸 앞을 F가 가리킨다.이러한 특성은 실제 큐의 구현에서 그대로 코드로 옮겨진다.
따라서 별도로 정리하고 이해해 둘 필요가 있다.
배열 기반의 큐라 하면 대부분의 경우 원형 큐를 의미한다고 봐도 무리가 아니다.
따라서 우리도 배열 기반의 큐를 대표하는 원형 큐를 구현하고자 한다.
그럼 먼저 헤더파일을 정의해 보겠다.
CircularQueue.h
#ifndef __C_QUEUE_H__
#define __C_QUEUE_H__
#define TRUE 1
#define FALSE 0
#define QUE_LEN 100
typedef int Data;
typedef struct _cQueue
{
int front; // 그림을 통해서 F라 표현했던 멤버
int rear; // 그림을 통해서 R이라 표현했던 멤버
Data queArr[QUE_LEN];
} CQueue;
typedef CQueue Queue;
void QueueInit(Queue * pq);
int QIsEmpty(Queue * pq);
void Enqueue(Queue * pq, Data data);
Data Dequeue(Queue * pq);
Data QPeek(Queue * pq);
#endif앞서 정의한 큐의 ADT를 기반으로 위의 헤더파일을 정의하였다.
그림에서 F와 R로 표현했던 변수를 위의 구조체에서는 각각 front와 rear로 이름 지었다.
이어서 헤더파일에 선언된 함수의 구현을 보일 차례인데, 그에 앞서 다음 함수를 먼저 소개하고자 한다.
이 함수는 간단하지만 원형 큐의 핵심이라 할 수 있다!
int NextPosIdx(int pos) // 큐의 다음 위치에 해당하는 인덱스 값 반환
{
if(pos == QUE_LEN-1)
return 0;
else
return pos+1;
}이는 큐의 다음 위치에 해당하는 배열의 인덱스 값을 반환하는 함수이다.
따라서 1을 전달하면 2를 반환하고, pos를 전달하면 pos+1을 반환한다.
그러나 큐의 길이보다 하나 작은 값, 즉 배열의 끝이 인자로 전달되면 0을 반환한다.
이것이 무엇을 의미하는가?
그렇다! F 혹은 R이 배열의 끝에 도달했으므로, 다시 맨 앞으로 이동해야 함을 의미한다.
즉 F와 R의 회전을 돕는 함수이다.
이제 원형 큐의 구현을 보이겠다.
CircularQueue.c
#include <stdio.h>
#include <stdlib.h>
#include "CircularQueue.h"
void QueueInit(Queue * pq) // 텅 빈 경우 front와 rear은 동일위치 가리킴
{
pq->front = 0;
pq->rear = 0;
}
int QIsEmpty(Queue * pq)
{
if(pq->front == pq->rear) // 큐가 텅 비었다면
return TRUE;
else
return FALSE;
}
int NextPosIdx(int pos)
{
if(pos == QUE_LEN-1) // 배열의 마지막 요소의 인덱스 값이라면
return 0;
else
return pos+1;
}
void Enqueue(Queue * pq, Data data)
{
if(NextPosIdx(pq->rear) == pq->front) // 큐가 꽉 찼다면
{
printf("Queue Memory Error!");
exit(-1);
}
pq->rear = NextPosIdx(pq->rear); // rear을 한 칸 이동
pq->queArr[pq->rear] = data; // rear이 가리키는 곳에 데이터 저장
}
Data Dequeue(Queue * pq)
{
if(QIsEmpty(pq))
{
printf("Queue Memory Error!");
exit(-1);
}
pq->front = NextPosIdx(pq->front); // front를 한 칸 이동
return pq->queArr[pq->front]; // front가 가리키는 데이터 반환
}
Data QPeek(Queue * pq)
{
if(QIsEmpty(pq))
{
printf("Queue Memory Error!");
exit(-1);
}
return pq->queArr[NextPosIdx(pq->front)];
}이번에는 우리가 구현한 원형 큐의 동작을 확인하기 위한 main 함수를 소개하겠다.
CircularQueueMain.c
#include <stdio.h>
#include "CircularQueue.h"
int main(void)
{
// Queue의 생성 및 초기화 ///////
Queue q;
QueueInit(&q);
// 데이터 넣기 ///////
Enqueue(&q, 1); Enqueue(&q, 2);
Enqueue(&q, 3); Enqueue(&q, 4);
Enqueue(&q, 5);
// 데이터 꺼내기 ///////
while(!QIsEmpty(&q))
printf("%d ", Dequeue(&q));
return 0;
}3. 큐의 연결 리스트 기반 구현
배열을 기반으로 큐를 구현하는 경우에는 몇 가지 고려할 사항이 있었다.
그래서 원형 큐를 소개했고, 또 큐가 꽉 찬 경우와 텅 빈 경우를 구분하는 방법도 소개하였다.
하지만 연결 리스트를 기반으로 구현하는 경우에는 의외로 신경 쓸 부분이 적다.
먼저 연결 리스트 기반 큐의 헤더파일을 소개하겠다.
ListBaseQueue.h
#ifndef __LB_QUEUE_H__
#define __LB_QUEUE_H__
#define TRUE 1
#define FALSE 0
typedef int Data;
typedef struct _node
{
Data data;
struct _node * next;
} Node;
typedef struct _lQueue
{
Node * front;
Node * rear;
} LQueue;
typedef LQueue Queue;
void QueueInit(Queue * pq);
int QIsEmpty(Queue * pq);
void Enqueue(Queue * pq, Data data);
Data Dequeue(Queue * pq);
Data QPeek(Queue * pq);
#endif위의 헤더파일에서 보이듯이 연결 리스트 기반의 큐에서도 원형 큐와 마찬가지로 front와 rear을 유지해야 한다.
enqueue 연산과 dequeue 연산이 이뤄지는 위치가 다르기 때문이다.
자! 그럼 연결 리스트 기반 큐의 동작형태를 간단하게나마 정리해보자.
처음 큐가 생성된 이후의 모습은 다음과 같다.
F와 R이 가리킬 대상이 없으니 초기에는 다음과 같이 NULL을 가리키게 하면 된다.
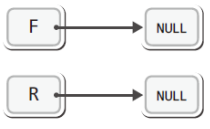
따라서 QueueInit함수는 다음과 같이 정의해야 한다.
void QueueInit(Queue * pq)
{
pq->front = NULL;
pq->rear = NULL;
}그리고 F가 가리키는 노드를 대상으로 dequeue 연산이 진행되니, 다음과 같이 판단할 수 있다.
"연결 리스트 기반의 큐가 비었다면, F에 NULL이 저장된다."이렇듯 R을 제외한 F만을 참조하여 큐가 비었는지 판단을 하면, 이후에 큐가 텅 비게 되는 경우에도 F만을 신경 쓰면 되게 때문에 여러모로 편리하다.
그럼 이어서 QIsEmpty함수를 정의하겠다.
int QIsEmpty(Queue * pq)
{
if(pq->front == NULL)
return TRUE;
else
return FALSE;
}이제 Enqueue함수를 정의할 차례인데, 이 경우에는 큐의 머리를 가리키는 front 뿐만 아니라 큐의 꼬리를 가리키는 rear도 있다는데 주의해야 한다.
이 때문에 노드의 추가과정이 둘로 나뉘기 때문이다.
그럼 다음 그림을 보면서 이와 관련된 설명을 진행하겠다.

위 그림에서 보이듯이, 첫 번째 노드가 추가 될 때에는 F뿐만 아니라 R도 새 노드를 가리키도록 설정해야 한다.
반면 두 번째 이후의 노드가 추가될 때에는 F는 변함이 없다.
대신 R이 새 노드를 가리키게 해야 하고, 노드간의 연결을 위해서 가장 끝에 있는 노드가 새 노드를 가리키게 해야 한다.
때문에 첫 번째 노드의 추가과정과 두 번째 이후 노드의 추가과정에는 차이가 있다.
그럼 이러한 내용을 근거로 Enqueue 함수를 정의해보자.
void Enqueue(Queue * pq, Data data)
{
Node * newNode = (Node*)malloc(sizeof(Node));
newNode->next = NULL;
newNode->data = data;
if(QIsEmpty(pq)) // 첫 번째 노드 추가라면
{
pq->front = newNode; // front가 새 노드를 가리키게 하고
pq->rear = newNode; // rear도 새 노드를 가리키게 한다.
}
else // 두 번째 이후의 노드 추가라면
{
pq->rear->next = newNode; // 마지막 노드가 새 노드를 가리키게 하고
pq->rear = newNode; // rear가 새 노드를 가리키게 한다.
}
}이제 마지막으로 Dequeue 함수를 정의할 차례인데, 이와 관련해서 다음과 같이 생각할 수도 있다.
"Enqueue 함수의 구현과 마찬가지로 노드의 삭제과정도 둘로 나뉠 거야!"하지만 그렇지 않다!
노드의 삭제과정에서 신경 쓸 부분은 F 하나이기 때문이다.
"그럼 R은 그냥 내버려둬도 되나요?"이 질문에 답을 얻기 위해서 다음 그림을 보자.

위 그림에서는 dequeue의 과정을 보이고 있다.
그림에서 보이는 dequeue의 과정을 정리하면 다음과 같다.
- F가 다음 노드를 가리키게 한다.
- F가 이전에 가리키던 노드를 소멸시킨다.때문에 위 그림의 상태에서 다시 한번 dequeue 연산을 진행하면 F와 R이 모두 6이 모두 저장된 노드를 가리키게 되어 다음 상태에 이르게 된다.
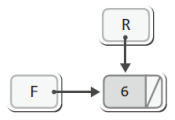
문제는 그 다음이다.
위 그림의 상태에서 다시 한 번 dequeue 연산을 하는 경우의 처리 방식이 문제이다.
만약에 앞서 하던 방식대로 처리한다면, 다시 말해서 F가 가리키는 대상을 그 다음 노드로 변경시키고, F가 이전에 가리키던 노드를 삭제한다면 다음의 상태가 된다.
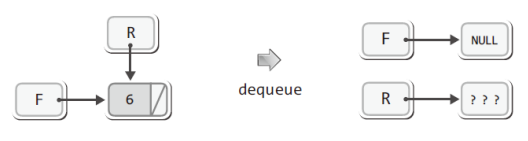
우선 F에 NULL이 저장되었음에 주목하자.
이는 자연스러운 결과이다.
F는 6이 저장된 노드를 참조하여 다음 노드의 주소 값을 얻게 되는데 그 값이 NULL이다.
그래서 F에는 NULL이 저장된다.
자! 그럼 위 그림의 결과에서 R에 NULL이 아닌 다른 값이 저장되어 있는데 이것이 문제가 되지는 않을까?
문제되지 않는다!
우리는 QIsEmpty 함수를 정의할 때에도 F에 저장된 값만을 참조하여 TRUE 또는 FALSE를 반환하도록 정의하였다.
이렇듯 큐가 텅 비었는지 확인할 때에도 F만을 참조하니, R에 쓰레기 값이 저장된 위의 상황은 문제되지 않는다.
그리고 굳이 R에 NULL을 넣을 필요가 없다면, dequeue의 과정은 둘로 나뉘지 않는다.
때문에 다음과 같이 Dequeue 함수를 간단히 정의할 수 있다
Data Dequeue(Queue * pq)
{
Node * delNode;
Data retData;
if(QIsEmpty(pq))
{
printf("Queue Memory Error!");
exit(-1);
}
delNode = pq->front; // 삭제할 노드의 주소 값 저장
retData = delNode->data; // 삭제할 노드가 지닌 값 저장
pq->front = pq->front->next; // 삭제할 노드의 다음 노드를 front가 가리킴
free(delNode);
return retData;
}이로써 연결 리스트를 기반으로 하는 큐의 구현도 끝났다.
그럼 설명하지 않은 QPeek 함수의 정의를 포함하여, 지금까지 설명한 함수의 정의를 한데 묶고, 학습의 편의를 위해서 앞서 보인 헤더파일도 다시 한 번 보이겠다.
ListBaseQueue.h
#ifndef __LB_QUEUE_H__
#define __LB_QUEUE_H__
#define TRUE 1
#define FALSE 0
typedef int Data;
typedef struct _node
{
Data data;
struct _node * next;
} Node;
typedef struct _lQueue
{
Node * front;
Node * rear;
} LQueue;
typedef LQueue Queue;
void QueueInit(Queue * pq);
int QIsEmpty(Queue * pq);
void Enqueue(Queue * pq, Data data);
Data Dequeue(Queue * pq);
Data QPeek(Queue * pq);
#endifListBaseQueue.c
#include <stdio.h>
#include <stdlib.h>
#include "ListBaseQueue.h"
void QueueInit(Queue * pq)
{
pq->front = NULL;
pq->rear = NULL;
}
int QIsEmpty(Queue * pq)
{
if(pq->front == NULL)
return TRUE;
else
return FALSE;
}
void Enqueue(Queue * pq, Data data)
{
Node * newNode = (Node*)malloc(sizeof(Node));
newNode->next = NULL;
newNode->data = data;
if(QIsEmpty(pq))
{
pq->front = newNode;
pq->rear = newNode;
}
else
{
pq->rear->next = newNode;
pq->rear = newNode;
}
}
Data Dequeue(Queue * pq)
{
Node * delNode;
Data retData;
if(QIsEmpty(pq))
{
printf("Queue Memory Error!");
exit(-1);
}
delNode = pq->front;
retData = delNode->data;
pq->front = pq->front->next;
free(delNode);
return retData;
}
Data QPeek(Queue * pq)
{
if(QIsEmpty(pq))
{
printf("Queue Memory Error!");
exit(-1);
}
return pq->front->data;
}다음은 큐를 테스트하기 위한 main 함수로써 앞서 원형 큐를 테스트할 때 정의한 main 함수와 헤더파일만 다르고 동일하다.
ListBaseQueueMain.c
#include <stdio.h>
#include "ListBaseQueue.h"
int main(void)
{
// Queue의 생성 및 초기화 ///////
Queue q;
QueueInit(&q);
// 데이터 넣기 ///////
Enqueue(&q, 1); Enqueue(&q, 2);
Enqueue(&q, 3); Enqueue(&q, 4);
Enqueue(&q, 5);
// 데이터 꺼내기 ///////
while(!QIsEmpty(&q))
printf("%d ", Dequeue(&q));
return 0;
}4. 덱(Deque)의 이해와 구현
큐를 설명하였으니, 이와 관련이 있는 덱(Deque)을 소개하고자 한다.
참고로 스택과 큐의 구조를 이해하고, 양방향 리스트까지 구현해본 경험이 있다면 덱의 구현은 매우 쉬운 일이다.
따라서 자세한 설명은 최대한 줄여서 덱을 소개해보겠다.
큐를 쉽게 설명해야 할 때, 다음 문장을 사용해서 개념을 한 번에 전달하려고 노력한다.
"큐는 뒤로 넣고 앞으로 빼는 자료구조!"이러한 느낌으로 덱을 한 문장으로 설명하면 다음과 같다.
"덱은 앞으로도 뒤로도 넣을 수 있고, 앞으로도 뒤로도 뺄 수 있는 자료구조!"이것을로 덱의 구조는 충분히 설명되었으리라 생각한다.
deque은 double-ended queue를 줄여서 표현한 것으로, 양방향으로 넣고 뺄 수 있다는 사실에 초점이 맞춰져서 지어진 이름이다.
어쨌든 덱은 양방향으로 넣고, 양방향으로 뺄 수 있는 자료구조이기에 스택과 큐의 특성을 모두 갖는, 혹은 스택과 큐를 조합한 형태의 자료구조로 이해되고 있다.
따라서 덱의 ADT를 구성하는 핵심 함수 네 가지의 기능은 다음과 같다.
- 앞으로 넣기
- 뒤로 넣기
- 앞에서 빼기
- 뒤에서 빼기그럼 이어서 위의 기능을 중심을 한 덱의 ADT를 정의하겟다.
물론 아래의 정의가 덱의 일반적인 ADT이다.

덱의 구현을 위해서 우선적으로 해야할 일은 헤더파일의 정의이다.
그런데 헤더파일을 정의하기 위해서는 구현할 덱의 구조를 결정해야 한다.
물론 덱도 배열을 기반으로, 연결 리스트를 기반으로 모두 구현이 가능하다.
하지만 우리는 덱의 구현에 가장 어울린다고 알려진 '양방향 연결 리스트'를 기반으로 덱을 구현할 것이다.
양방향 연결 리스트가, 단방향 연결 리스트보다 덱의 구현에 더 잘 어울리는 이유는 다음 함수의 구현과 관련이 있다.
Data DQRemoveLast(Deque * pdeq);위의 함수는 꼬리에 위치한 노드를 삭제하는 함수인데, 노드가 양방향으로 연결되어 있지 않으면, 꼬리에 위치한 노드의 삭제는 간단하지 않다.
때문에 덱의 구현에 있어서 양방향 연결 리스트는 매우 좋은 선택이라 할 수 있다.
그럼 양방향 연결 리스트 기반의 덱을 위한 헤더파일을 정의하겠다.
Deque.h
#ifndef __DEQUE_H__
#define __DEQUE_H__
#define TRUE 1
#define FALSE 0
typedef int Data;
typedef struct _node
{
Data data;
struct _node * next;
struct _node * prev;
} Node;
typedef struct _dlDeque
{
Node * head;
Node * tail;
} DLDeque;
typedef DLDeque Deque;
void DequeInit(Deque * pdeq);
int DQIsEmpty(Deque * pdeq);
void DQAddFirst(Deque * pdeq, Data data); // 덱의 머리에 데이터 추가
void DQAddLast(Deque * pdeq, Data data); // 덱의 꼬리에 데이터 추가
Data DQRemoveFirst(Deque * pdeq); // 덱의 머리에서 데이터 삭제
Data DQRemoveLast(Deque * pdeq); // 덱의 꼬리에서 데이터 삭제
Data DQGetFirst(Deque * pdeq); // 덱의 머리에서 데이터 참조
Data DQGetLast(Deque * pdeq); // 덱의 꼬리에서 데이터 참조
#endif위의 헤더파일에 정의된 구조체 Node를 보면 양방향 연결 리스트를 기반으로 덱이 구현됨을 알 수 있고, 구조체 DLDeque을 보면 head와 tail이 각각 리스트의 머리와 꼬리를 가리키게 됨을 알 수 있다.
즉 다음 구조의 양방향 연결 리스트를 기반으로 덱을 구현할 생각이다.
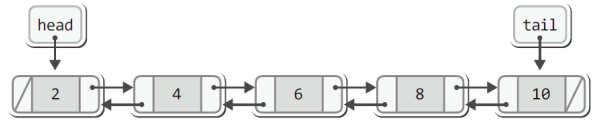
이는 전에도 구현해본 경험이 있는 자료구조이다.
때문에 이전에 구현한 내용을 참조하면 쉽게 덱을 구현할 수 있다.
비록 이어서 바로 코드를 공개하지만, 직접 구현해보는 것도 나쁘지 않다.
Deque.c
#include <stdio.h>
#include <stdlib.h>
#include "Deque.h"
void DequeInit(Deque * pdeq)
{
pdeq->head = NULL;
pdeq->tail = NULL;
}
int DQIsEmpty(Deque * pdeq)
{
if(pdeq->head == NULL)
return TRUE;
else
return FALSE;
}
void DQAddFirst(Deque * pdeq, Data data)
{
Node * newNode = (Node*)malloc(sizeof(Node));
newNode->data = data;
newNode->next = pdeq->head;
if(DQIsEmpty(pdeq))
pdeq->tail = newNode;
else
pdeq->head->prev = newNode;
newNode->prev = NULL;
pdeq->head = newNode;
}
void DQAddLast(Deque * pdeq, Data data)
{
Node * newNode = (Node*)malloc(sizeof(Node));
newNode->data = data;
newNode->prev = pdeq->tail;
if(DQIsEmpty(pdeq))
pdeq->head = newNode;
else
pdeq->tail->next = newNode;
newNode->next = NULL;
pdeq->tail = newNode;
}
Data DQRemoveFirst(Deque * pdeq)
{
Node * rnode = pdeq->head;
Data rdata = pdeq->head->data;
if(DQIsEmpty(pdeq))
{
printf("Deque Memory Error!");
exit(-1);
}
pdeq->head = pdeq->head->next;
free(rnode);
if(pdeq->head == NULL)
pdeq->tail = NULL;
else
pdeq->head->prev = NULL;
return rdata;
}
Data DQRemoveLast(Deque * pdeq)
{
Node * rnode = pdeq->tail;
Data rdata = pdeq->tail->data;
if(DQIsEmpty(pdeq))
{
printf("Deque Memory Error!");
exit(-1);
}
pdeq->tail = pdeq->tail->prev;
free(rnode);
if(pdeq->tail == NULL)
pdeq->head = NULL;
else
pdeq->tail->next = NULL;
return rdata;
}
Data DQGetFirst(Deque * pdeq)
{
if(DQIsEmpty(pdeq))
{
printf("Deque Memory Error!");
exit(-1);
}
return pdeq->head->data;
}
Data DQGetLast(Deque * pdeq)
{
if(DQIsEmpty(pdeq))
{
printf("Deque Memory Error!");
exit(-1);
}
return pdeq->tail->data;
}DequeMain.c
#include <stdio.h>
#include "Deque.h"
int main(void)
{
// Deque의 생성 및 초기화 ///////
Deque deq;
DequeInit(&deq);
// 데이터 넣기 1차 ///////
DQAddFirst(&deq, 3);
DQAddFirst(&deq, 2);
DQAddFirst(&deq, 1);
DQAddLast(&deq, 4);
DQAddLast(&deq, 5);
DQAddLast(&deq, 6);
// 데이터 꺼내기 1차 ///////
while(!DQIsEmpty(&deq))
printf("%d ", DQRemoveFirst(&deq));
printf("\n");
// 데이터 넣기 2차 ///////
DQAddFirst(&deq, 3);
DQAddFirst(&deq, 2);
DQAddFirst(&deq, 1);
DQAddLast(&deq, 4);
DQAddLast(&deq, 5);
DQAddLast(&deq, 6);
// 데이터 꺼내기 2차 ///////
while(!DQIsEmpty(&deq))
printf("%d ", DQRemoveLast(&deq));
return 0;
}