[알고리즘 기법] Meet In The Middle

2시간 거리에 살던 여자친구를 사귀던 시절, 대부분 데이트를 여자친구 동네 주변에서 했던 기억이 있다. 서로 지쳐서 헤어질 때쯤 만약 여자친구가 중간 지점에서 자주 만나줬더라면 우리 관계가 더 오래갔을까 하는 생각이 문득 들었었다.

Meet In The Middle이란?

GeeksforGeeks에 따르면 Meet In The Middle(이하 MITM) 알고리즘은 Brutefroce 알고리즘을 사용해야하지만 경우의 수가 Bruteforce를 사용하기에 조금 클 때 사용된다고 한다. 즉 이름이 암시하듯 Bruteforce를 사용하되 이를 분할해서 연산의 수를 최소화하는 것이다. 예로 N 크기 배열 원소의 모든 조합을 고려해야하는 문제가 있다고 하자. 이때 N이 20이라면 $2^{20}$(약 100만)개의 연산을 하면 된다. 이럴 때는 일반 채점 서버의 초당 연산 수가 억대이므로(1~3억)출처 문제가 발생하지 않는다. 하지만 만약 N이 40이라면? 이때는 경우의 수가 $2^{40}$(약 1조)로 시간 내에 연산을 수행할 수 없다. 이런 경우를 위해 사용되는 기법이 MITM인 것이다.
더불어 MITM은 분할정복과 비슷한 형태를 취하지만, 분할정복은 다수의 작은 문제 해결을 통해 커다란 하나의 문제를 해결하는 반면 MITM은 작은 문제 해결과 더불어 $+\alpha$의 연산이 필수적이라는 점에서 차이가 있다.

백준 예시

나는 MITM 기법을 백준 1208번: 부분수열의 합에서 처음 접하게 되었다. 이 문제도 위의 설명과 마찬가지로 $2^{40}$개의 경우의 수가 있다. 문제의 구제적인 설명은 아래와 같다.(이때 부분수열은 연속적인 부분집합일 필요가 없으므로 모든 경우의 수를 확인해야한다.)

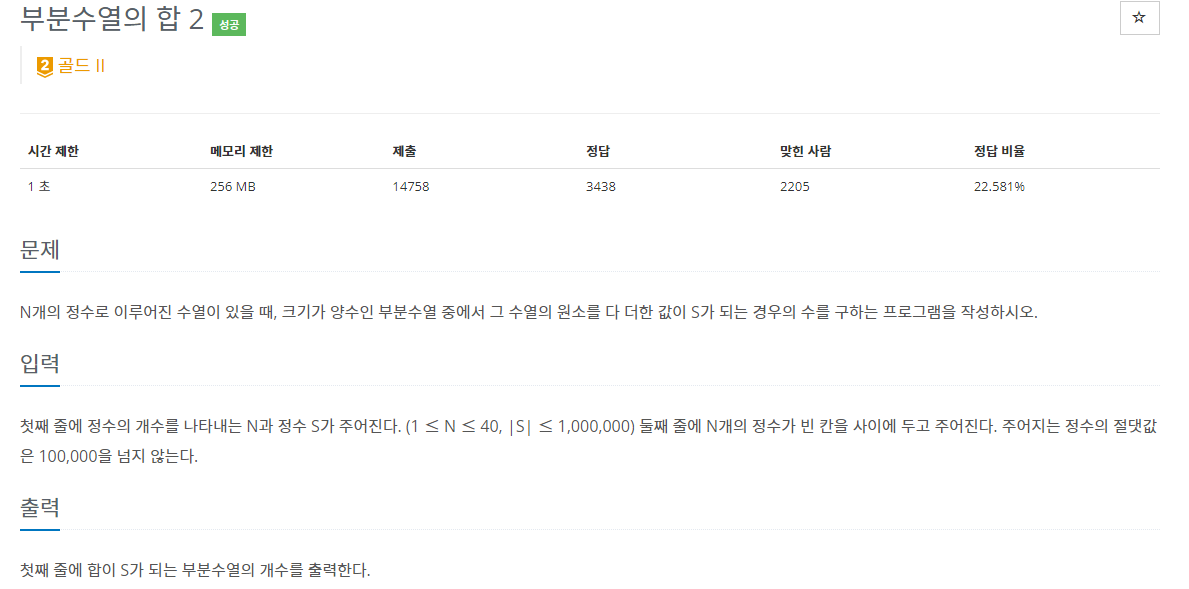
그렇다면 이 문제를 어떻게 풀 수 있을까? MITM 전략은 흔히 주어진 배열을 둘로 나누어 Bruteforce 알고리즘을 실행하게 된다. 따라서 O($2^{N}$) 알고리즘이 2개의 O($2\times2^{\frac{N}{2}}$) 알고리즘으로 변하게 된다. 즉 이 문제의 경우 $2^{40}$이 $2\times2^{20}$이 되므로 굉장히 효과적으로 시간 복잡도를 줄여준다고 할 수 있다.
그럼 이 이후에 어떻게 문제를 해결할지가 중요한데, 여기서부터는 문제마다 다르므로 사고력이 필요하다. 해당 문제의 경우는 주어진 배열을 각각 A, B의 배열로 나누어 탐색할 때, A의 각 결과의 수를 맵에 저장하고 B를 탐색할 때는 맵에 저장된 정보와 대조하는 식으로 답을 산출한다.

구체적인 예를 보자. 주어진 배열이 {1, 1, 2, 3}이고 N=4, S=3이라고 가정하자. 이때 주어진 배열을 반으로 나누면 크기 2의 배열 2개가 나오므로 A는 {1, 1}, B는 {2, 3}이다. A가 {1, 1}일 때 나올 수 있는 경우의 수는 {1, 1, 2}이므로 map[1] = 2, map[2]=1을 저장을 한다. 이후 B의 경우의 수 {2, 3, 5} 각각에 대해 map[$S-B_{i}$]를 확인해주면 두 반쪽 배열 원소의 합로 S를 몇변 구할 수 있는지 산출할 수 있다. 물론 $A$, $B$에 대해 $A_{i}$나 $B_{i}$ 자체가 S인 경우도 고려를 해주어야한다.

보다 대표적인 예

보다 다양하게 응용을 하기 위해 다른 예시를 살펴보자. MITM에 대해 온라인 검색을 하다보면 아래와 같은 문제가 가장 흔한 것 같다(출처: GeeksForGeeks).

위의 백준 문제와는 달리 해당 문제는 Map을 사용하지 않는다(적어도 해당 페이지에는 그렇지 않다). 이는 문제의 색이 조금 다르기 때문이다. 간략하게 설명하자면 위의 문제는 합이 S인 경우만 생각하면 되어서 괜찮지만, 해당 문제는 합이 S가 되지 않는다면, S보다 작은 합 중 가장 근접한 수를 출력해야해서 Bruteforce 이후에 O(1) 연산이 불가능하다. 따라서 GeeksForGeeks에서는 이분탐색을 통한 정답 탐색을 추천한다. 이때 연산 수는 $2^{\frac{N}{2}}\times\log(2^{\frac{N}{2}})$가 되므로 시간복잡도는 O($2^{\frac{N}{2}}N$) 이 된다.
이와 같은 기법을 위의 백준 문제에 사용했다가는 봉변을 당할 수 있음을 주의해야한다. 위의 문제는 부분수열의 합이 S가 되는 경우의 수의 합을 원하므로 이분 탐색을 하여 A에서 $S-B_{i}$를 찾게 되면 전후로 동일한 원소가 있는지 확인해주어야한다. 따라서 백준 질문에 주어진 테스트케이스를 돌리면 O($2^{N}$)의 시간복잡도를 갖게 된다.

1208번 풀이: https://www.acmicpc.net/source/35573339

출처

Quora - What is meet in the middle algorithm w.r.t. competitive programming?
GeeksforGeeks - Meet In The Middle