[알고리즘 기법] 비트필드를 이용한 DP

스핑크스의 유명한 수수께끼 "목소리는 같지만 발이 4개가 되기도 하고 2개가 되기도 하고 3개가 되기도 하는 것은 무엇인가?"에 대한 다른 답안을 생각해볼 수 있는가? 이를 고안하기는 생각보다 힘들다. 필자는 10분의 구글링을 통해서 아무런 답을 찾지 못했으니까. 개인적으로는 아래 사진과 같이 카메라도 해답이 될 수 있다고 생각한다.

비트필드를 이용한 DP란?

위의 답이 무리라고 생각하는가? 무리가 맞다. 하지만 뭐 사람이라고 노년에 꼭 지팡이를 사용한다는 보장도 없으니 너그러히 넘어가자. 요점은 개발자라면, PS 능력을 키우려면 같은 것을 다르게 보고 응용할 능력이 있어야한다는 것이다.
우선 비트필드가 무엇인지 알아보자. 일단 이 글을 읽는 사람이라면 비트 연산을 모르는 사람은 없으리라 생각한다. 만약 있다면 기초적인 비트 연산과 관련하여 찾아보고 오기를 권장한다. PS에서 비트연산의 가장 기초적인 응용은 완전탐색에서의 응용이다. 예컨데 $N$개의 정수가 있고, 이의 부분집합의 합이 $S$가 될 수 있는지 묻는 문제가 있다고 하자. 많은 해결 방법이 있겠으나, $N$이 너무 크지 않다면 비트연산을 통한 완전탐색을 생각해볼 수 있다. $\lbrack1<<0, 1<<N)$까지의 숫자를 사용하면 모든 부분집합의 경우의 수를 탐색할 수 있다. 비트필드는 이렇듯 비트가 모여 만들어진(즉 각 비트가 의미를 갖는) 구조체다. 참고로 비트연산이 중요한지 궁금한 분이 있다면 아래 리눅스 소스코드의 스냅샷을 참고하길 바란다. 비트연산은 효율성이 극대화되어야 하는 경우에 사용되며 특히 리눅스 커널에서 굉장히 많이 사용된다. 아래 사진은 TASK의 종류를 16진수 비트필드로 표현한 것이다.

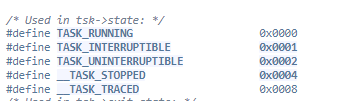
이것을 DP에서 어떻게 사용할 수 있을까? 뭐 사용 방법이야 굉장히 다양할 수 있다. 일반적으로 DP 캐시(메모)에 비트필드를 저장할 수도 있고, 비트필드를 DP 캐시의 인덱스로 사용하는 방법이 있겠다. 아래 예시는 후자에 대한 예시를 다루고 있다.

백준 예시

백준 1562번: 계단 수는 비트필드를 이용한 DP의 클래식한 문제라고 한다. 문제 스펙을 살펴보자.

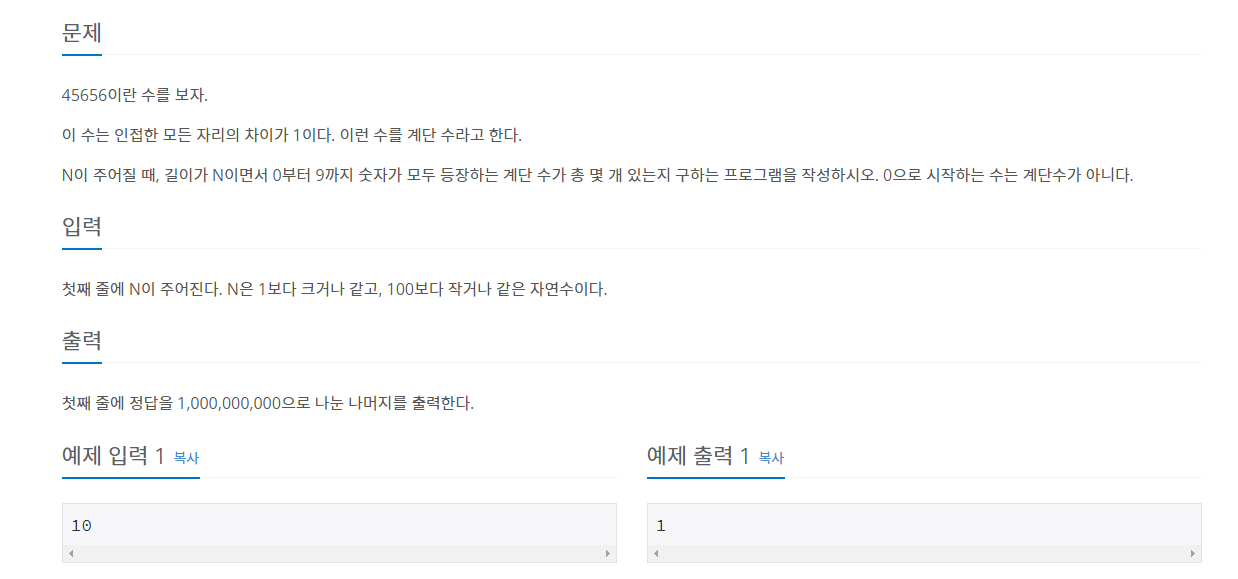
해당 문제보다 쉬운 백준 10844번: 쉬운 계단 수는 2차원 캐시 $DP\lbrack N \rbrack\lbrack 10 \rbrack$가 있을 때 1에서 8까지 다음의 점화식으로 해결할 수 있다(1과 9는 별도로 처리해주면 된다).

$DP\lbrack i]\lbrack j] = (DP\lbrack i-1]\lbrack j+1] +DP\lbrack i-1]\lbrack j-1])\mod1000000000, (i, j \ge1)$

그렇다면 1562번 문제는 어떻게 해결하면 될까. 이 문제에서는 0에서 9까지의 모든 수가 포함되어 있는 경우만 결과값에 1을 추가해야한다. 그런즉 각 원소를 지나갈 때마다 위의 $j$값을 지나갔다는 표시를 해주어야하는데, 이를 배열로 기록하기는 너무 많은 시간과 공간이 소요된다. 그렇다면 이것을 비트필드로 저장하면 좋겠는데, 문제의 핵심은 이를 어떻게 풀어나갈 것인지에 달려있다.
필자는 가장 먼저 DP에 비트필드 값을 저장하는 쪽으로 생각을 했었다. 하지만 이렇게 하면 문제가 생긴다. 지금까지 발견한 계단 수를 $count$, 발견한 숫자(0-9)를 기록한 비트필드를 $digit$이라고 할 때, $\{count, digit\}$ 페어를 담고 있는 캐시 $DP\lbrack i]\lbrack j]$에서 특정 $i$, $j$값을 위의 점화식으로 계산산다고 가정해보자. 곰곰히 생각해보면 $DP\lbrack i-1]\lbrack j+1]$와 $DP\lbrack i-1]\lbrack j-1]$는 높은 확률로 다른 $digit$값을 가지고 있다(각각 다른 j에서 올테니까). 따라서 비트필드를 인덱스로 사용하는 방법을 생각해보아야한다(사실 다른 고수님들의 블로그를 많이 참고하였다).
각 $j$를 방문할 때마다 $digit$에 하당 비트를 켜주는 방식으로 연산을 하면, $j$는 총 10개(0~9)이므로 $1<<10$개의 경우의 수가 있음을 알 수 있다. 따라서 캐시를 $DP\lbrack N ]\lbrack 10]\lbrack 1<<10]$으로 바꾸어 주자. 이때 $DP\lbrack i]\lbrack j]\lbrack k]$의 값을 계산한다고 하면 $DP\lbrack i-1]\lbrack j\pm1]\lbrack k\&\sim(1<<j)]$ 값을 여기에 추가할 수 있음을 알 수 있다. 따라서 이를 고려한 점화식을 세우면 해당 문제를 해결할 수 있다. 이에 대한 수도 코드는 아래와 같다.

FOR i 2...N
    FOR j 0...9
    	FOR k 0...(1<<10)-1
            j==0, j==9에 대한 예외 처리
            IF j!=9 AND j!=0
            	DP[i][j][k|1<<j] = (DP[i][j][k|1<<j]+DP[i-1][j-1][k]
            			+DP[i-1][j+1][k]) % 1000000000
            ENDIF
        ENDFOR
    ENDFOR
ENDFOR