모든 사진 자료에 관한 출처는 아래 알튜비튜 - 튜터링에 있음을 밝힙니다.
https://github.com/Altu-Bitu/Notice

🌐그래프

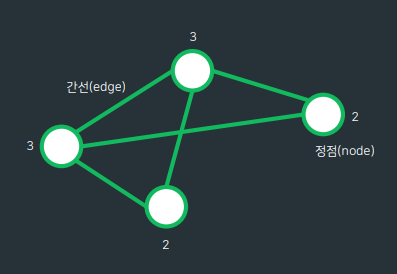
• 정점과 그 정점을 연결하는 간선으로 이루어진 자료구조
• 간선의 방향은 단방향(방향 그래프)나 양방향(무방향 그래프)로 나뉨
• 간선에 가중치가 있을 수 있음

📚그래프 용어

• degree(차수) : 무방향 그래프에서 정점에 연결된 간선의 수
• 무방향 그래프의 총 차수(degree)의 합 -= 간선의 수 x 2 ex) 3+3+2+2=5x2
• indegree : 방향 그래프에서 해당 정점으로 들어오는 간선의 수
• outdegree : 방향 그래프에서 해당 정점에서 나가는 간선의 수
• 방향 그래프의 총 차수(indegree,outdegree)의 합 = 간선의 수 -> 들어오거나 나가는 간선 중 하나만 count되기 때문!

🕎그래프 경로

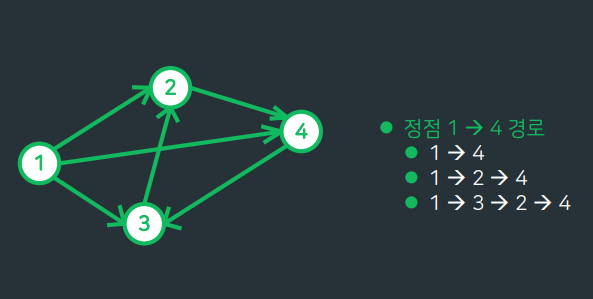
• 경로는 여러개일 수 있다.
• 사이클(cycle) : 한 정점에서 다시 동일한 정점으로 돌아오는 경로 (ex. 3->2->4)

🔩그래프 구현

1. 인접행렬

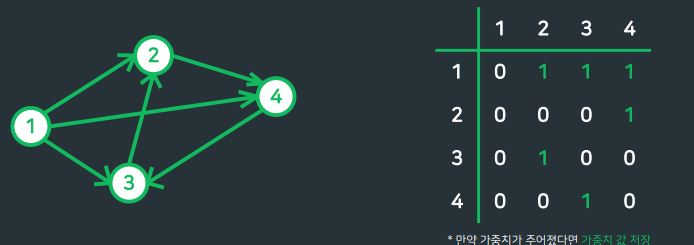
• 두 정점 간의 연결관계를 N*N 크기의 행렬(2차원배열)로 나타냄
• 두 정점 i-j 간의 연결관계확인 : O(1)
• 특정 노드와 연결되어 있는 모든 노드 확인 : O(N)
• 공간 복잡도 : O(N2)
  -> 정점이 많아지면 사용불가 (메모리초과)

2. 인접리스트

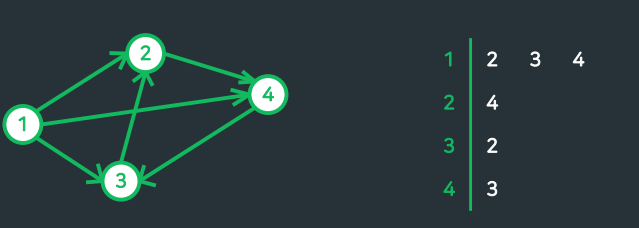
• 각 정점에 연결된 정점들을 리스트(1차원 배열)에 담아 보관
• 두 정점 i-j 간의 연결 관계 확인 : O(min(degree(i),degree(j)) // i,j중 더 낮은 차수
• 특정 노드(i)와 연결되어 있는 모든 노드 확인: O(degree(i)) //i의 차수 만큼.
• 공간복잡도 : O(N + E) //정점의 수 + 간선의 수

Q. 왜 O(E)가 아니지?
A. 이차배열이라 그런가

인접행렬 vs 인접 리스트

인접행렬

• 정점 사이의 연결 관계(간선)이 많을경우
• 특정 정점과 정점의 연결 관계를 많이 확인해야 하는 경우

인접리스트

• 정점 사이의 연결관계(간선)이 적은 경우
• 연결된 정점들을 탐색해야 하는 경우

🔭그래프 탐색

DFS(깊이 우선 탐색)

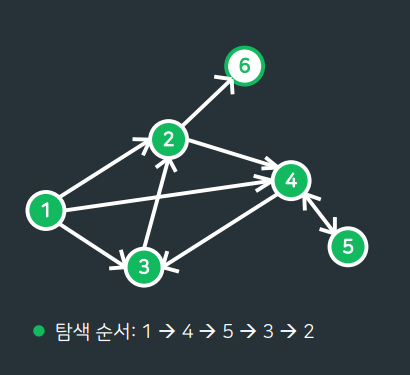
• 최대한 깊게 탐색 후 빠져 나옴
• 한 정점을 깊게 탐색해서 빠져 나왔다면, 나머지 정점 계속 동일하게 탐색
• 스택 (stack), 재귀 함수로 구현

BFS(너비 우선 탐색)

• 자신의 자식들부터 순차적으로 탐색
• 순차 탐색 이후, 다른 정점의 자식들 탐색
• 큐(queue)로 구현

DFS,BFS 특징

• 모든 노드를 방문하고자 하는 경우엔 DFS,BFS 상관 X
• 가중치가 주어지거나 특정 경로를 찾아야 할때는 DFS
• 두 노드 사이의 최단 거리를 찾을 때는 BFS(ex.미로찾기)
  -> BFS는 현재 노드에서 가장 가까운 곳(자식노드)부터 탐색하기 때문!
• 그래프가 단방향으로 주어지는지, 양방향으로 주어지는지 잘 살펴보자!

📌대표문제

BOJ) 1260 :DFS와 BFS

미로

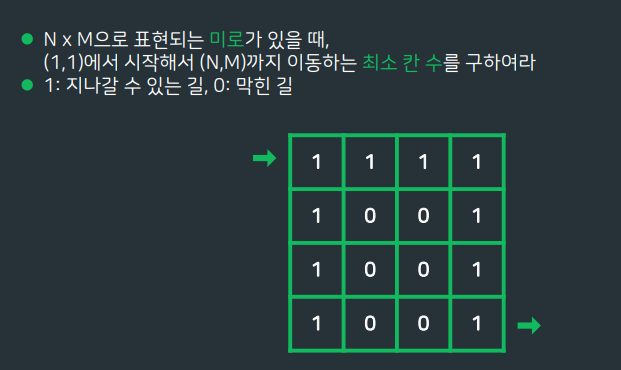
1. BFS 풀이
   
2. DFS 풀이
   

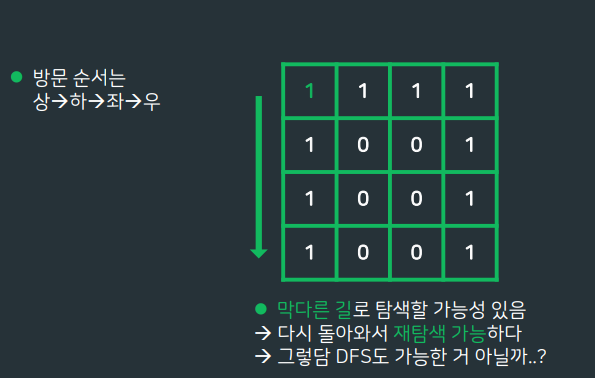
다른 미로를 살펴본다면 ...?

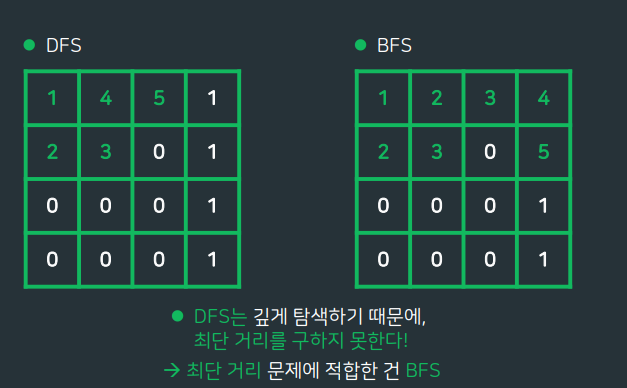
DFS의 3번째칸은 BFS의 3번째 칸보다 뒤처진다. 따라서 최단경로를 구하기 위해서는 반드시 BFS로 풀어야한다!

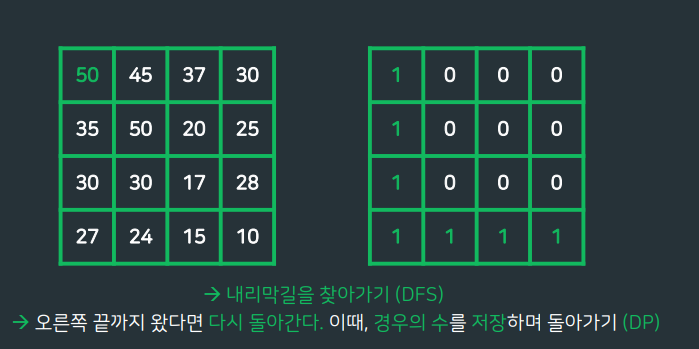
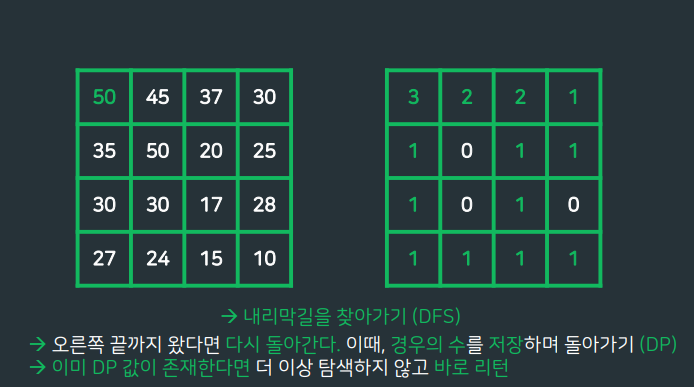
가능한 이동 경로의 개수

BFS,DFS 는 완전탐색 알고리즘이므로 시간초과. 따라서 DP배열을 적절하게 같이 활용하여 주어야함. DP배열에 목적지까지 도달하는 경우의수를 저장하자!