모든 사진 자료에 관한 출처는 아래 알튜비튜 - 튜터링에 있음을 밝힙니다.
https://github.com/Altu-Bitu/Notice

모든 사진 자료에 관한 출처는 아래 알튜비튜 - 튜터링에 있음을 밝힙니다.
https://github.com/Altu-Bitu/Notice
🥏동적계획법
- 특정 범위까지의 값을 구하기 위해 이전 범위의 값을 활용하여 효율적으로 값을 얻는 기법
- 이전 범위의 값을 저장함으로써 시간적,공간적 효율을 얻음
💹피보나치수열
피보나치 함수를 재귀함수로 구현하게 될 경우
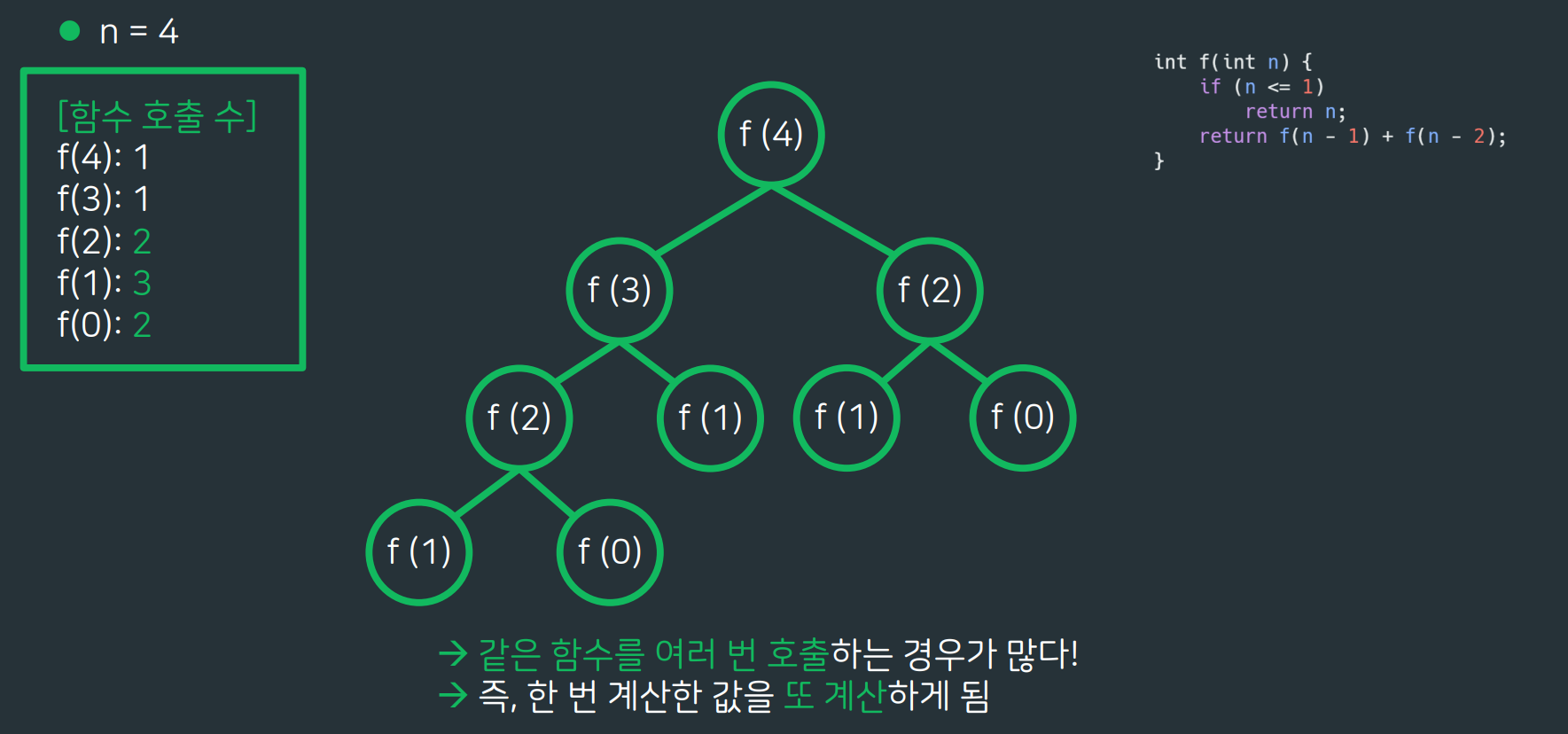
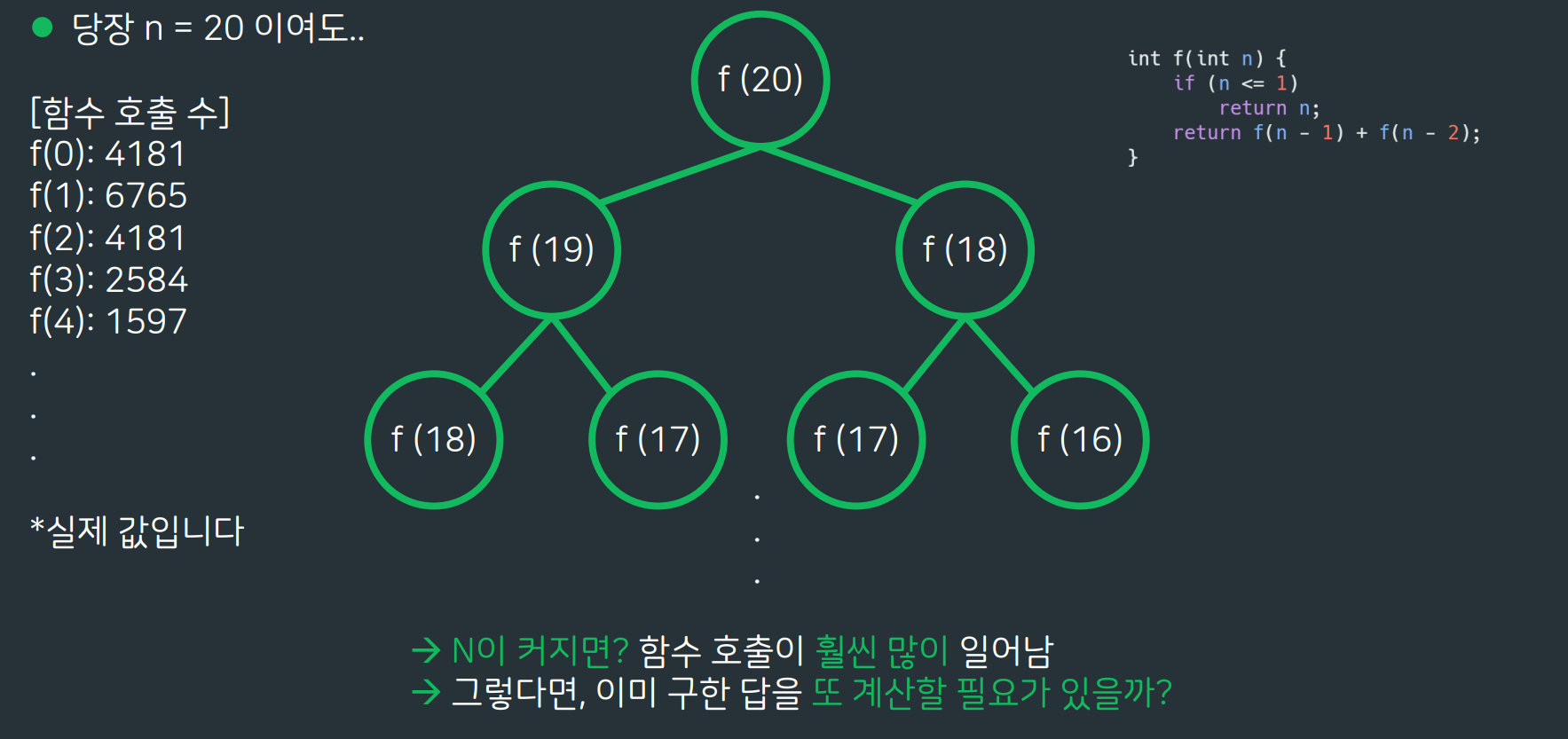
💾Memorization
- 이전에 구해둔 값을 저장해서 중복 계산을 방지
- 이전 범위의 답을 구하면, 바로 배열에 저장해 놓자!
- 시간과 공간면에서 모두 효율적!

Top-down 방식
int dp[100];
int fibo(int n) {
if (n <= 1)
return n;
if (dp[n]) // 이미 값이 존재한다면
return dp[n];
return dp[n] = fibo(n - 1) + fibo(n - 2);
}-> 구하려하는 문제를 작은 문제로 분할하며 탐색. 재귀함수활용
Bottom-up 방식
int n;
cin >> n;
dp[0] = 0;
dp[1] = 1;
for (int i = 2; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
cout << dp[n];-> 이미 알고있는 작은 문제부터 원하는 문제까지 탐색. Top-down보다 속도빠름!
💡동적계획법의 적용
- 주어진 문제를 부분 문제로 나누었을때, 부분 문제의 답을 통해 주어진 문제의 답을 도출할 수 있을때 활용.
- 부분 문제의 답을 여러번 구해야할때
- 즉, 한번 계산한 값을 다시 사용해야 할때.
🔥점화식
- 인접한 항들 사이의 관계식
- 동적 계획법 문제를 풀 때는, 점화식을 미리 세우고 풀면 좋다!
- 이전 값들을 통해 DP(현재)를 정의하자.
📗대표문제
BOJ) 12865 평범한 배낭

접근
- K까지의 무게를 인덱스로 나타냄
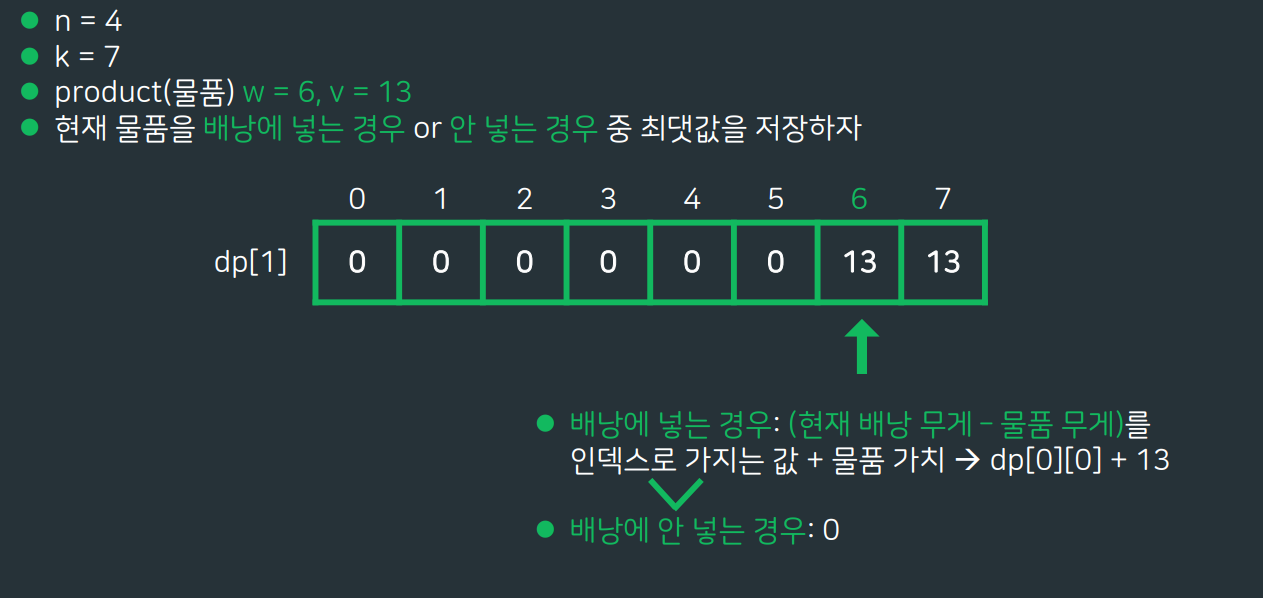
- 현재 물품을 배낭에 넣는 경우 or 안 넣는 경우 중 최댓값을 저장
- 배낭에 넣으려면 ?
-> 현재 물품만큼 배낭에 추가되는 것! 그런데 현재 인덱스가 배낭의 최대무게인데?
->[현재 배낭 무게 - 물품무게]인 배낭무게에서의 최대 가치값 + 현재 물품 가치값 - 배낭에 안 넣는 경우는?
-> 현재 배낭 무게에 저장된 정답을 그대로 사용하면 됨!
이해
dp[A][B]=C 는 A번째 물건까지 왔고, 가방의 무게가 B일때, 가방에 담긴 물건들의 가치는C 입니다. 라는 의미다. 즉 i번째 물품을 넣을거고, 가방의 무게가 j일때 가방이 갖는 최대 가치는 기존에 탐색했던 물건들로 현재물건의 무게를 뺀 무게의 가방에서의 최대가치값에서 현재물건을 가방에 넣는 경우의 가치값과 기존에 탐색했었던 물건들로만 무게 j를 만드는 경우 (변화X경우)의 가치값중 더 큰 값이 된다.
👻 점화식을 세워보자!
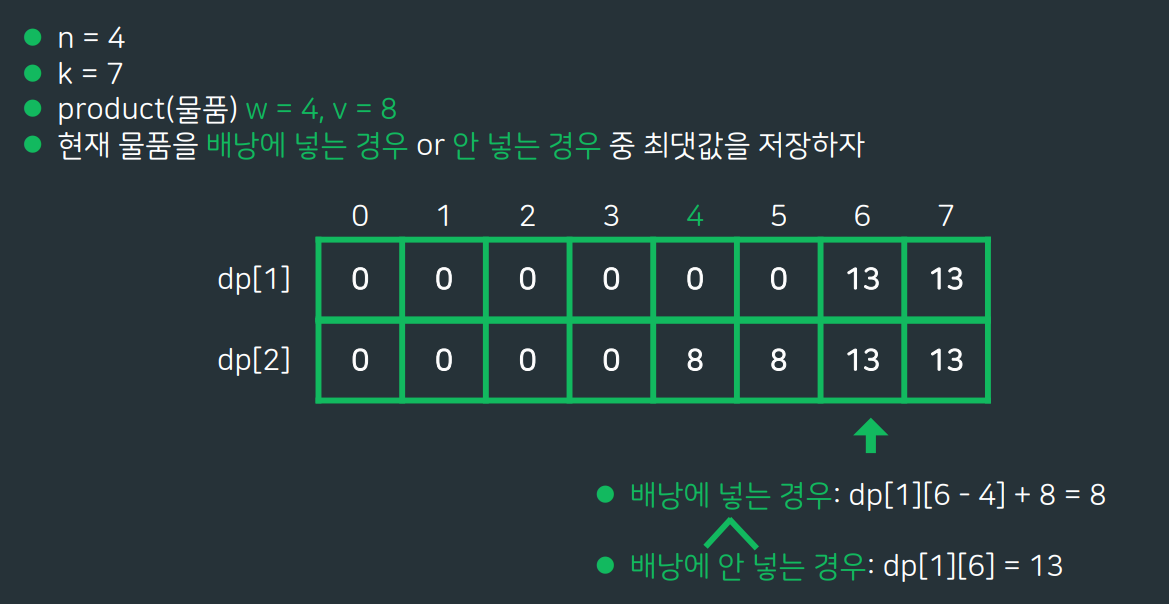
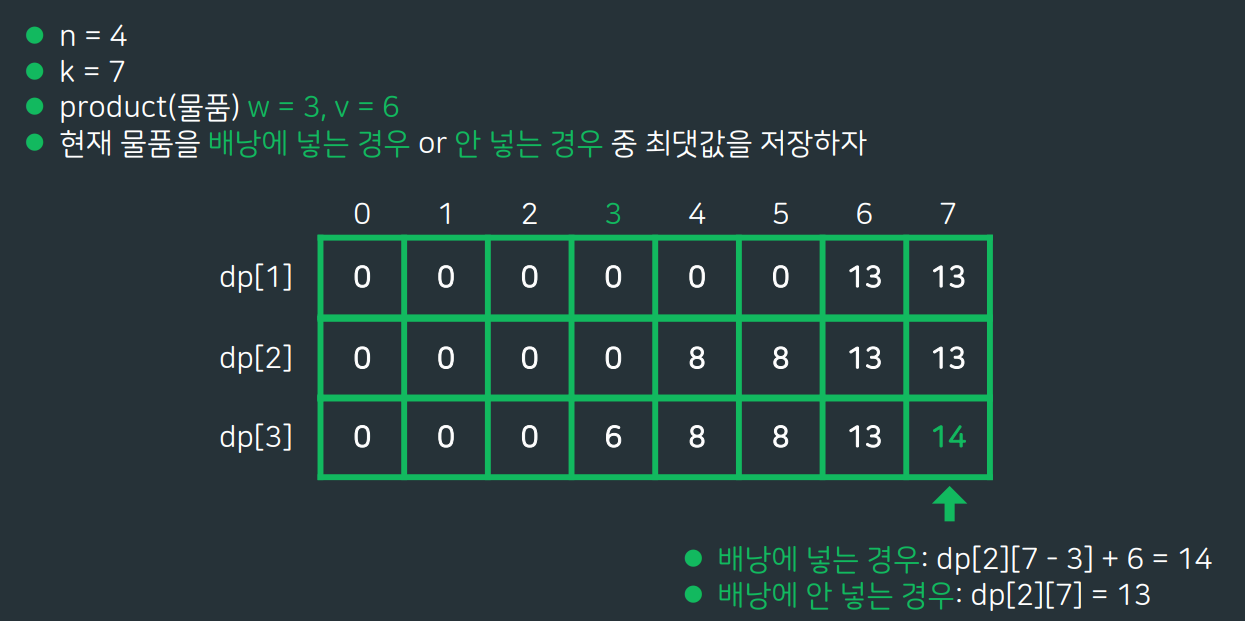
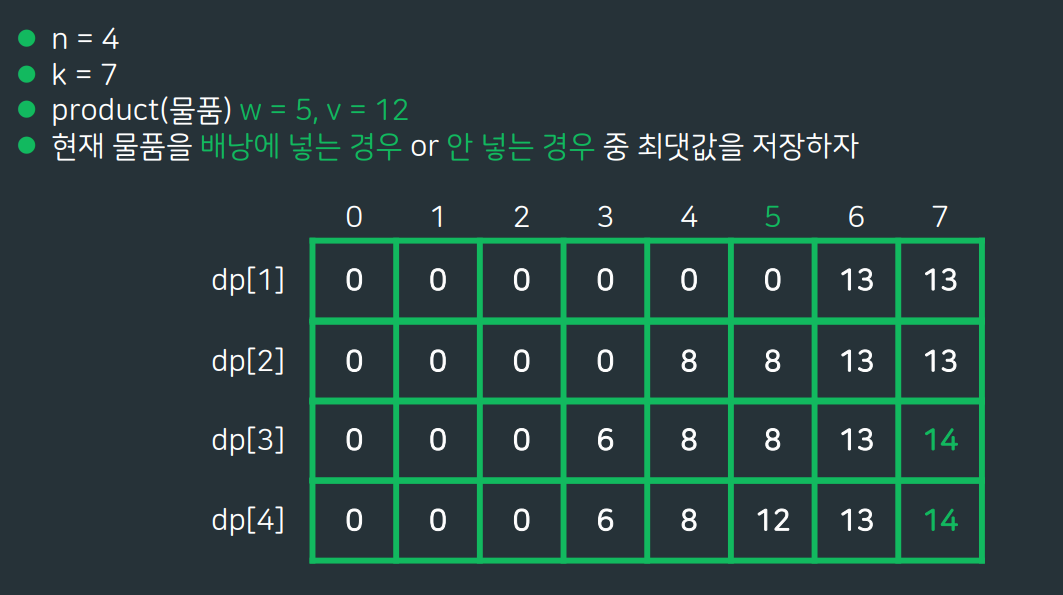

MAX 부분이 현재 물건을 가방에 넣을지,말지 판단하는 부분이 된다. 전자가 더 크다면 현재 물건을 가방에 넣는다는 것이고, 후자가 더 크다면 넣지 않는다는 뜻이 된다.
//2차원 dp 활용 냅색
int knapsack_2(int n, int k, vector<info>& product) {
vector<vector<int>> dp(n + 1, vector<int>(k + 1, 0));
for (int i = 1; i <= n; i++) { //각 물품에 대해, i: 물품 번호, j: 최대 배낭 무게
for (int j = 1; j < product[i].w; j++) //우선 해당 물품을 배낭에 넣을 수 없는 경우
dp[i][j] = dp[i - 1][j]; //그 전 물품에 대한 현재 무게의 최댓값 저장
for (int j = product[i].w; j <= k; j++) //해당 물품을 배낭에 넣는게 가능한 경우
dp[i][j] = max(dp[i - 1][j - product[i].w] + product[i].v, dp[i - 1][j]); //배낭에 넣는 경우와 안 넣는 경우 중 최댓값 저장
}
return dp[n][k];
}Q. 그렇다면 왜 2차원 DP를 사용할까? 1차원 DP로 하면 안될까?
그 전까지의 물품정보만 사용해야 하기 때문에 1차원 DP로는 안된다. 지금처럼 증가하면서 검사할때, 1차원 DP를 사용하게 되면, 해당 물품을 또 사용하는 경우가 생길 수 있다.
따라서 2차원을 사용하며, 각 물품을 행으로 구분하여 중복을 방지한다. 사실 1차원 DP로도 풀이가 가능하긴하다. 우리가 2차원 DP를 사용한 이유는 해당 물품을 여러번 사용하는 걸 방지하게 위함이었다. 그렇다면 지금처럼 증가하는게 아니라 무게를 감소하면서 계산한다면?
뒤에서부터 채워지므로 중복사용을 방지할 수 있다.
BOJ) 9251 LCS
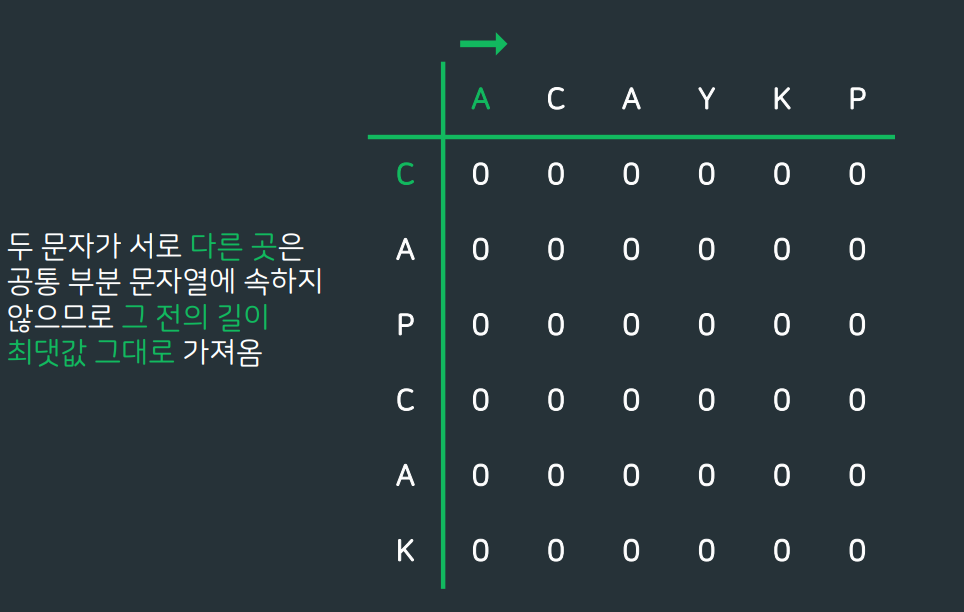
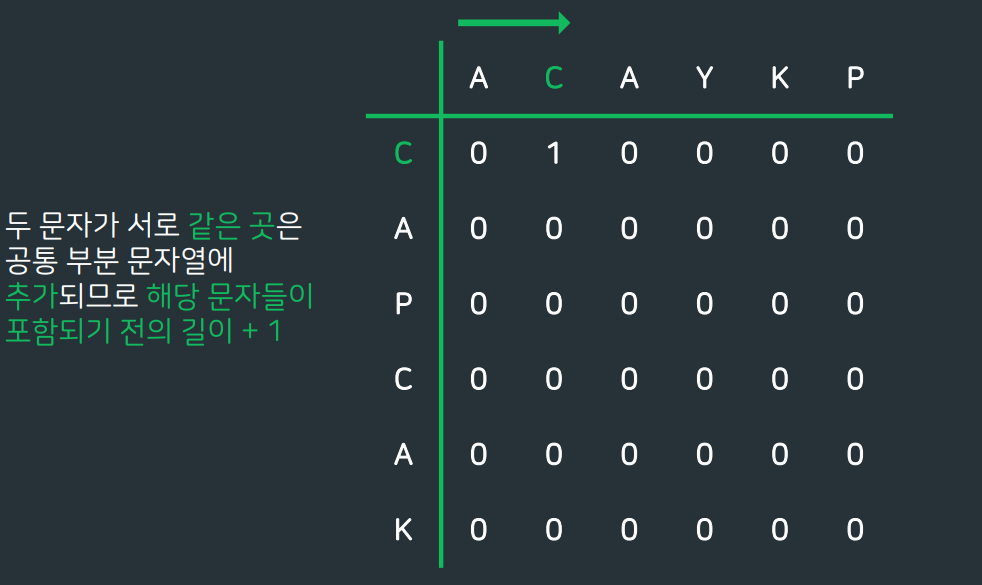


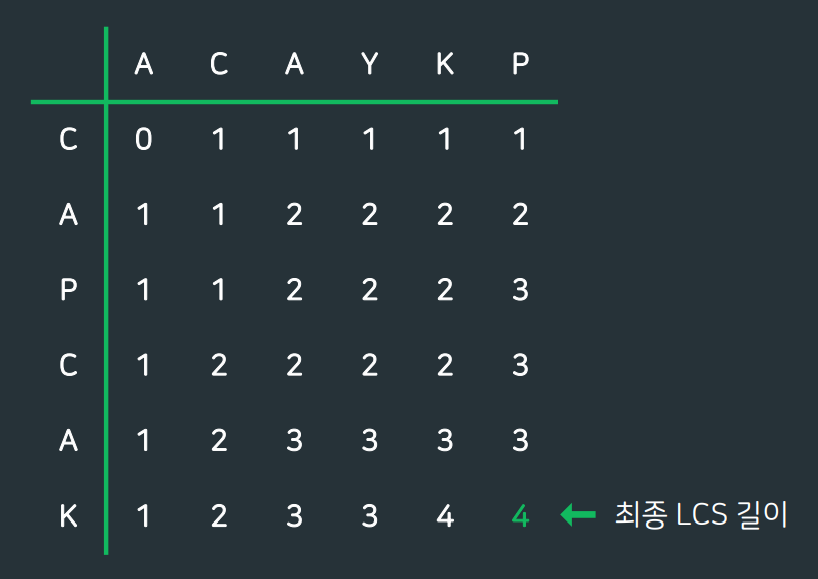
✨마무리
- 이전의 답을 저장하고, 계속 사용하며 현재 답을 구하는 동적계획법
- 입력범위가 나름 크다(보통 1000~1,000,000)이보다 더크다면 그리디 알고리즘 고려
- 마지막 인덱스에서 내려가는 Top-down, 처음 인덱스부터 올라가는 Bottom-up 방식 존재
- 문제에 따라 1차원 혹은 2차원 테이블(DP배열) 사용
- 점화식만 세우면 구현은 쉬움!
- LIS, 냅색, LCS는 동적계획법으로 푸는 대표적 문제 & 방식
- 따라서 세 유형의 풀이는 다른 동적 계획법 문제에서 많이 응용됨.
🎯📳📽🎥🎬📼🛒🥅🥏🎛🧫🗑📥📝🗓🖇
⚜🔰🔬🔭▶➡α✨💷📉🗞🔖📹📝🗝🖥⌨
✒📤🧾📜📗📕📘💡💾⛏🛠🔑🔏🔊🌈🔥🚩💫❓❗🔰♻✅✔🟥🟧🟨🟩🟦🟪🔺🖼🎞🎨🎗🔑⚠❔🔀↪➰💱🔴🔴🟠🟡🟢🔵🟣🟤⚫🗨🗝🔑🔨🔐🛠🎬🕯📸🔖👾👻✔👑💎🔭🔎