모든 사진 자료에 관한 출처는 아래 알튜비튜 - 튜터링에 있음을 밝힙니다.
https://github.com/Altu-Bitu/Notice

🕎분할정복
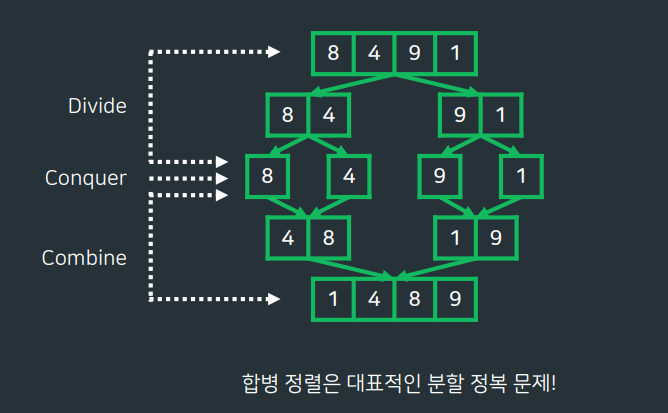
- 한 번에 해결할 수 없는 문제를 작은 문제로 분할하여 해결하는 알고리즘 ex)합병정렬
- 큰문제 -> 작은 문제 ->Top-down 접근!
- 주로 재귀함수로 구현
- 분할 방법에 따라 시간 복잡도는 천차만별
- 입력범위 N이 큰편
- 크게 3단계로 이루어짐
- Divide : 문제 분할
- Conquer : 쪼개진 작은 문제 해결
- Combine : 해결된 작은 문제들을 다시 합침

분할 정복을 활용해서 해결한다면❓
▶O(logN) 만에 power computation 문제를 해결할 수 있다!
long long power(int n, int k) {
if (k == 1) //Conquer
return n;
//Divide + Combine
if (k % 2 == 0) //지수가 짝수
return power(n * n, k / 2);
else //지수가 홀수
return n * power(n * n, (k-1) / 2);
}💎퀵정렬(Quick sort)
- 피봇을 기준으로 배열을 둘로 나눈뒤 정렬
- 시간복잡도는 일반적으로 O(nlogn)
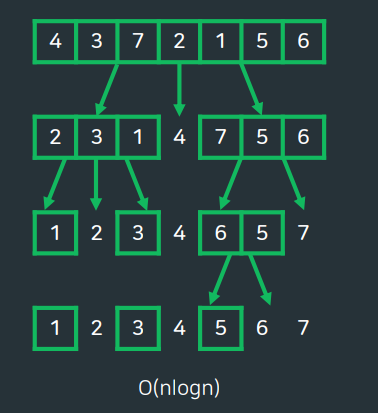
- 피봇의 선택 방법에 따라 최악의 경우 O(N2)의 시간복잡도가 될 수 있음.
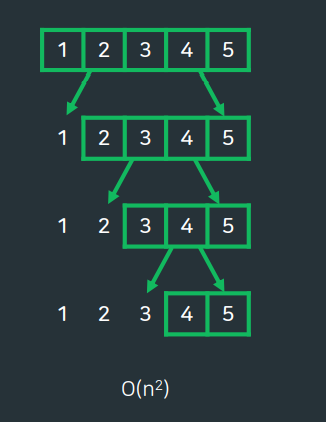
- 정렬과정
- 배열에서 원소 하나(pivot) 선택
- 배열의 왼쪽엔 pivot보다 작은 원소, 오른쪽엔 pivot보다 큰 원소 배치
- 왼쪽,오른쪽 배열에 대해 1~2 과정을 반복
- 배열의 크기가 0또는 1이되면 종료
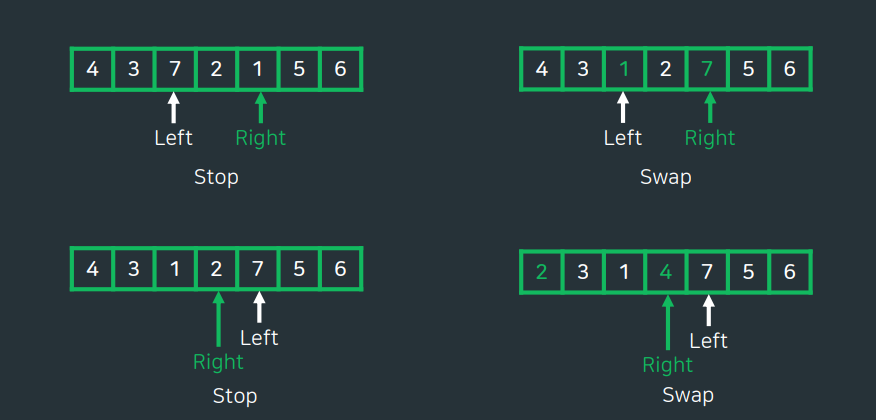
📝퀵정렬 과정
- pivot의 다음 위치를
Left, 범위의 마지막 위치를Right로 설정.
- 아직 완벽히 양분되지 않은 그룹의 맨 왼쪽 요소를 pivot으로 설정한다.
- Left가 가리키는 값이 pivot보다 클때까지 오른쪽으로 이동.
- Right가 가리키는 값이 pivot보다 작거나 같을때까지 왼쪽으로 이동.
- 두 포인터가 모두 멈추면 각 포인터가 가리키는 원소를 swap
- Left < Right 일동안 2~3 과정 반복
- 만일 Left 와 Right가
교차하면 Right가 가리키는는 원소와 pivot이 가리키는 원소를 swap
Q. Left,Right가 교차했다는 것의 의미
A. Left 는 왼쪽 끝에서 시작하여 pivot보다 커지면 멈추고 Right는 우측끝에서 시작하여 pivot보다 작아지면 멈춘다. 따라서 left <->right의 교차가 일어났다는 것은 left 좌측은 모두 pivot보다 작은 값이라는 것을 의미하고, Right의 우측은 모두 pivot보다 큰 값이라는 것을 의미한다. 따라서 본 상태에서 pivot <-> Right 를 교환해주면 pivot의 왼쪽에는 pivot보다 작은 값, pivot의 오른쪽에는 pivot보다 큰 값들이 위치해있게 된다.
📗대표문제
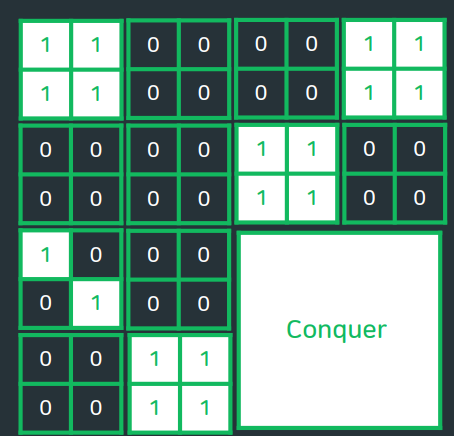
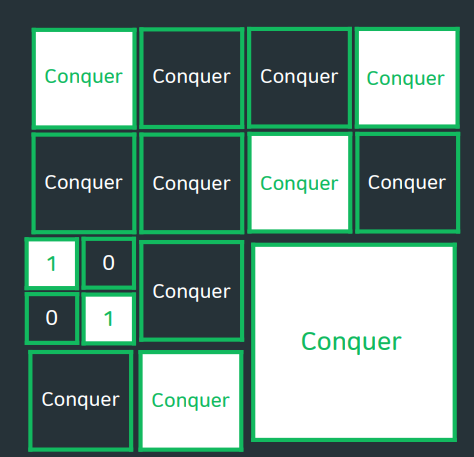
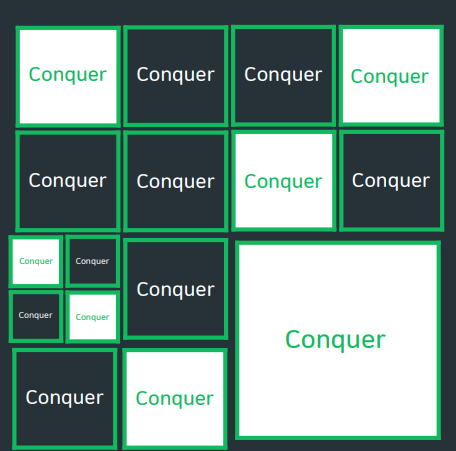
BOJ) 2630 : 색종이 만들기



BOJ) 4256 : 후위순회



✨결론
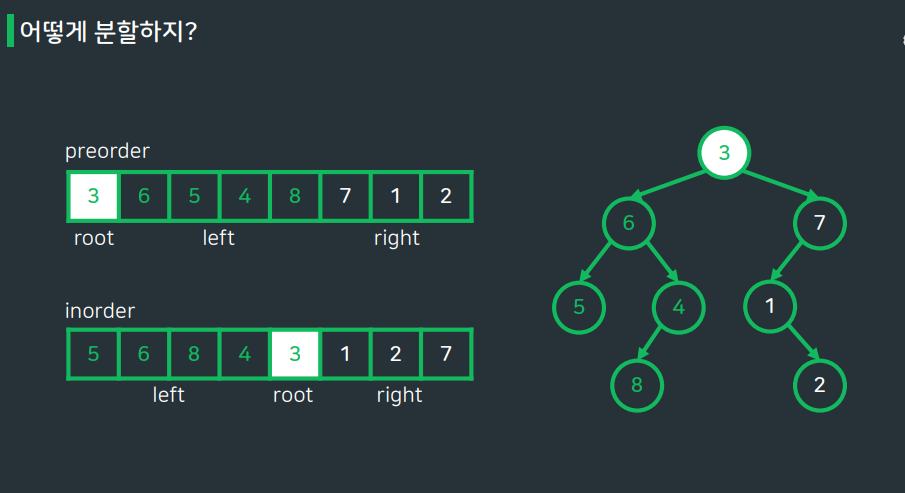
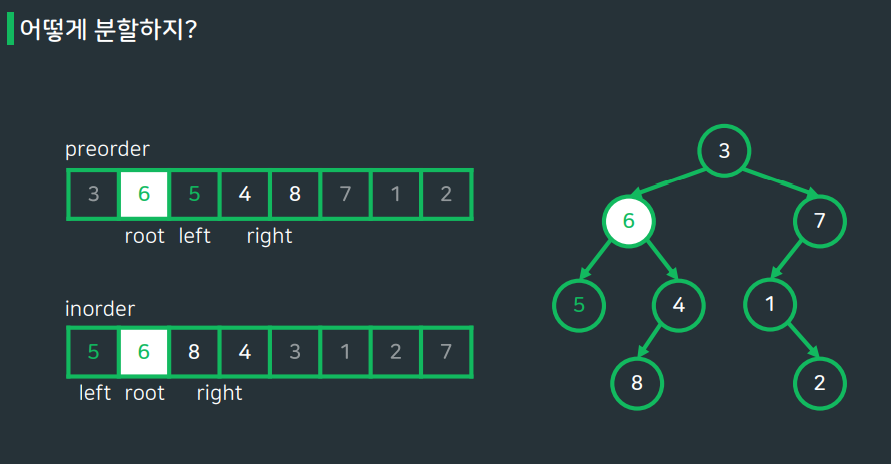
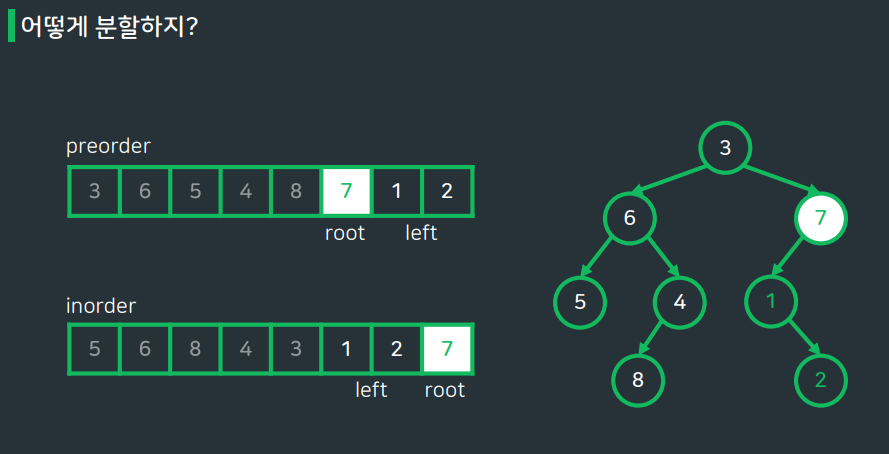
preorder (전위순회)
- 부분 트리의 root는 해당 부분 트리 구간의 맨 왼쪽
- root 이후에 왼쪽 서브트리의 노드와 오른쪽 서브트리의 노드가 이어진다.
▶ root의 위치는 알 수 있지만, 왼쪽/오른쪽 서브트리가 나뉘는 경계는 알수 없다.
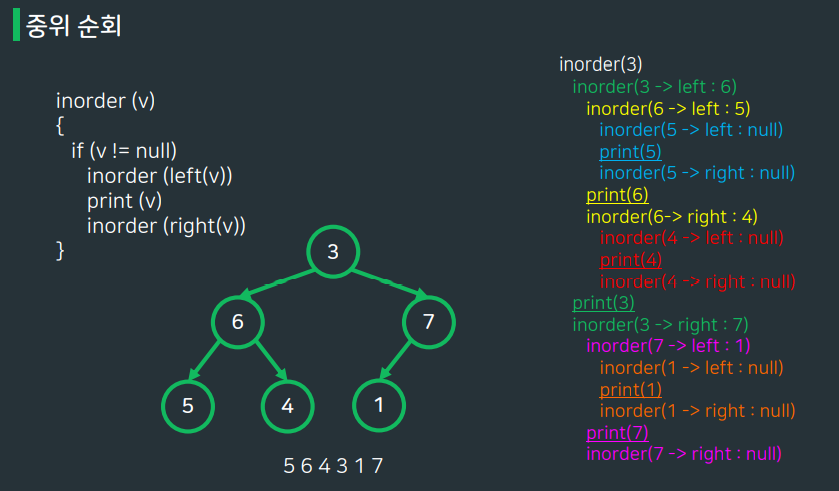
Inorder (중위순회)
- 부분 트리의 root를 기준으로 왼쪽에는 왼쪽 서브트리가, 오른쪽에는 오른쪽 서브 트리가 위치한다.
▶ root의 위치만 알면 왼쪽, 오른쪽 서브 트리의 노드를 알 수 있지만, root의 위치는 알 수 없다.
preorder로 루트 노드를 파악하고, Inorder로 왼쪽,오른쪽 서브트리를 나누자!

👾마무리
- 문제에 반복되는 연산이 보이거나 (ex.별찍기) N이 아주 크다면 분할 정복 생각하기!
- 단순 계산 문제라면 N은 long long 범위까지 들어올 수 있음.
Divide,Conquer,Combine연산이 어떤것일지 먼저 생각하기.- 구현 방법에 따라 시간복잡도가 다양. 잘못 구현했다면, 분할 정복임에도 시간초과가 발생할 수 있음.
- 재귀 함수를 구현할 때에는 무한루프에 빠지지 않도록 기저조건을 확실히하기.
이것도 알아보세요!
- 입력이 이미 또는 거의 정렬된 상태라면, Quick sort의 효율성이 떨어지는건 직접 눈으로 확인했습니다! 그렇다면, 이런상황에서 Quick sort의 효율성을 확보하기 위해서는 어떻게 해야할까요?
