1비트 가산기와 n비트 가산기

Verilog code는 아래 Git 링크에 업로드 해놓음

Git Link

목차

1. 1비트 가산기
   • 반가산기 (Half Adder)
     • 반가산기 진리표
   • 전가산기 (Full Adder)
     • 전가산기 진리표
2. n비트 가산기
   • 리플 캐리 가산기 (Ripple Carry Adder)
   • n비트 전가산기 (n bit Full Adder)
3. ALU (Arithmetic Logic Unit)

---

1비트 가산기

반가산기 (Half Adder)

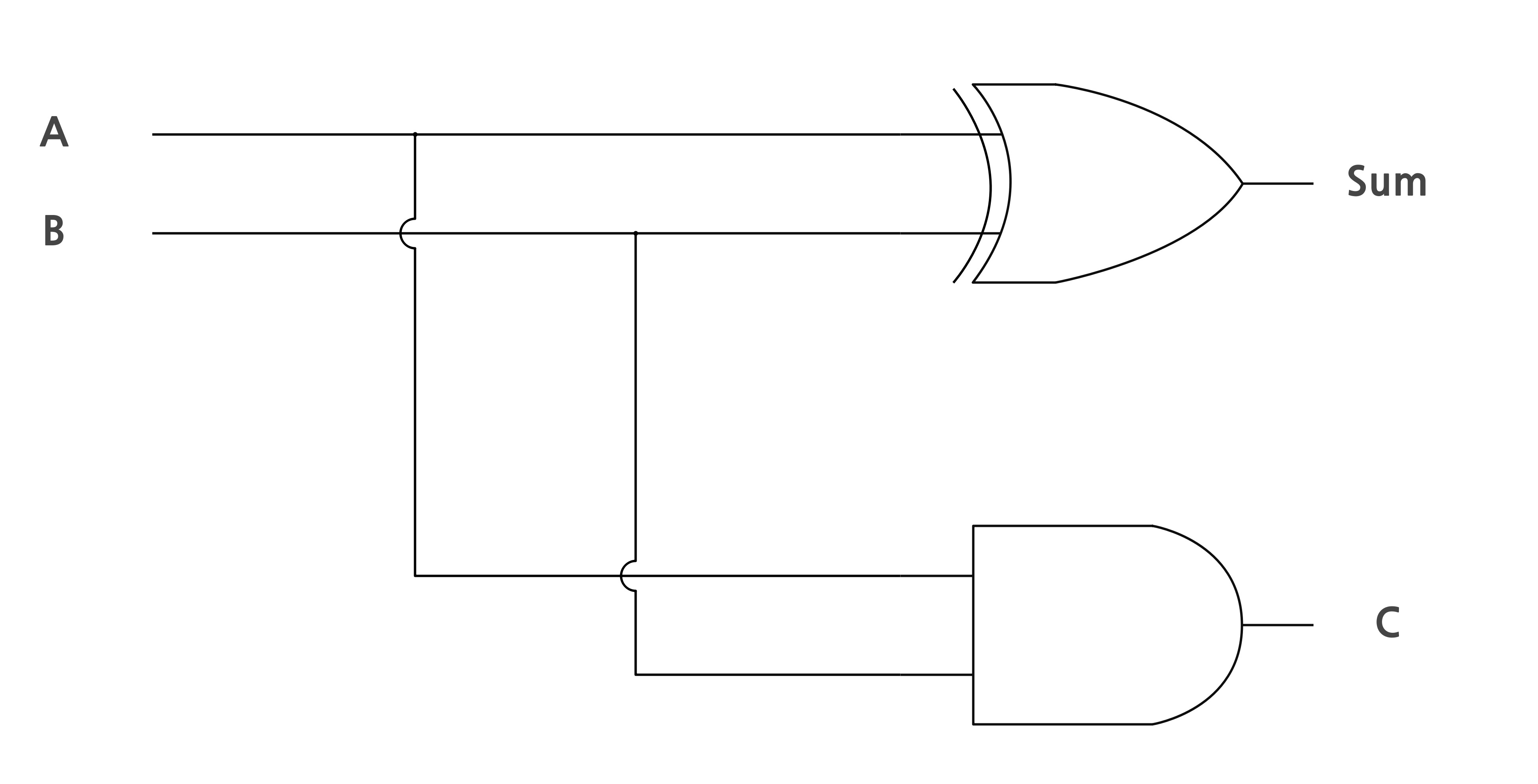
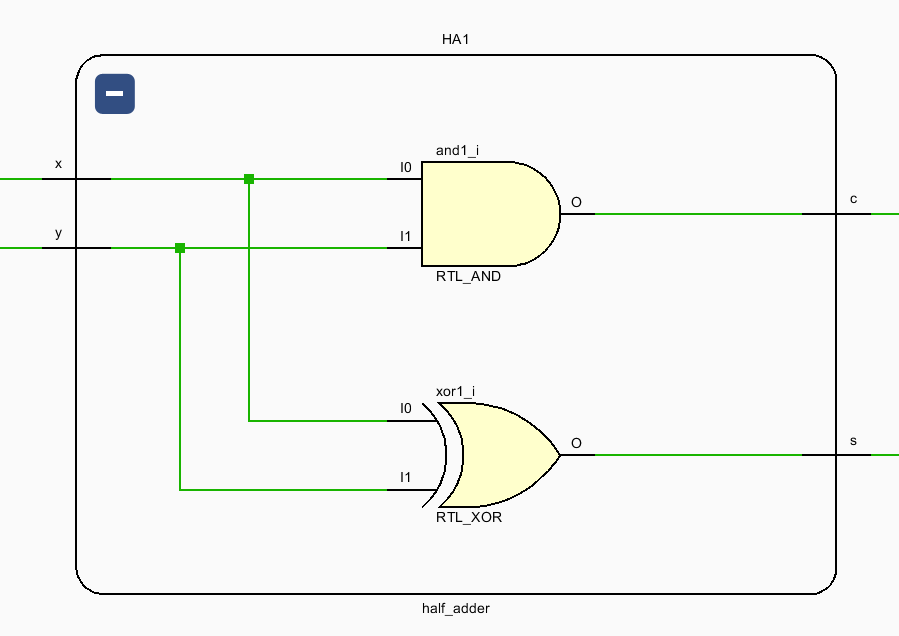
반가산기는 두 개의 1비트 이진수를 더하여 합(Sum)과 자리올림(Carry)을 생성한다.

• 합(Sum): 입력 A와 B의 XOR 결과
• 자리올림(Carry): 입력 A와 B의 AND 결과

반가산기 진리표

입력 A	입력 B	합 (Sum)	자리올림 (Carry)
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

---

전가산기 (Full Adder)

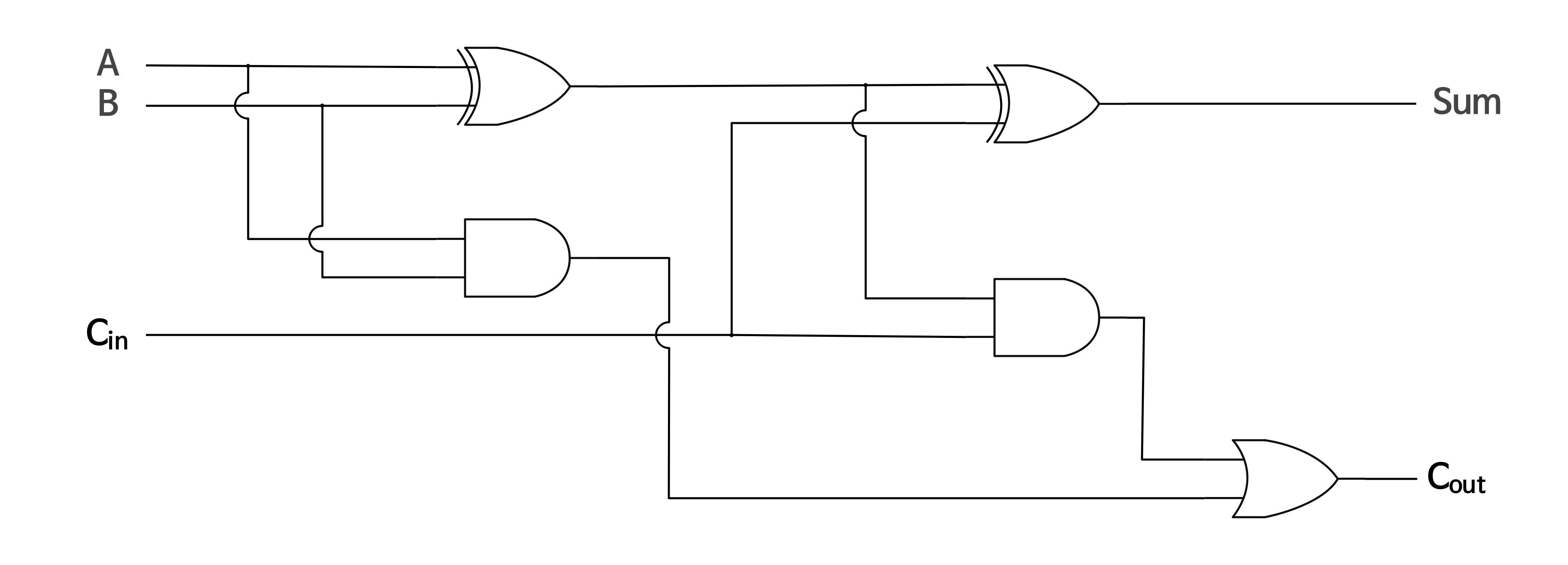
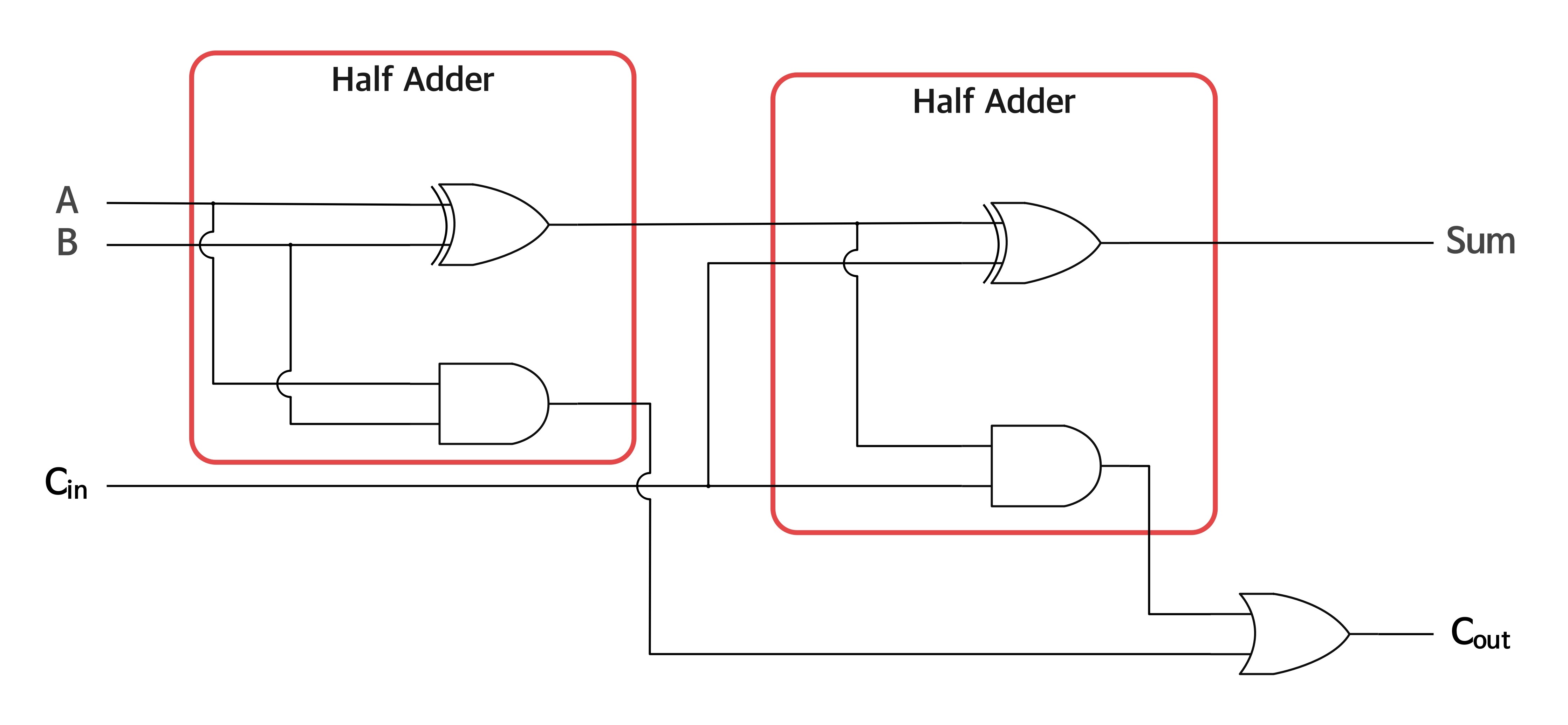
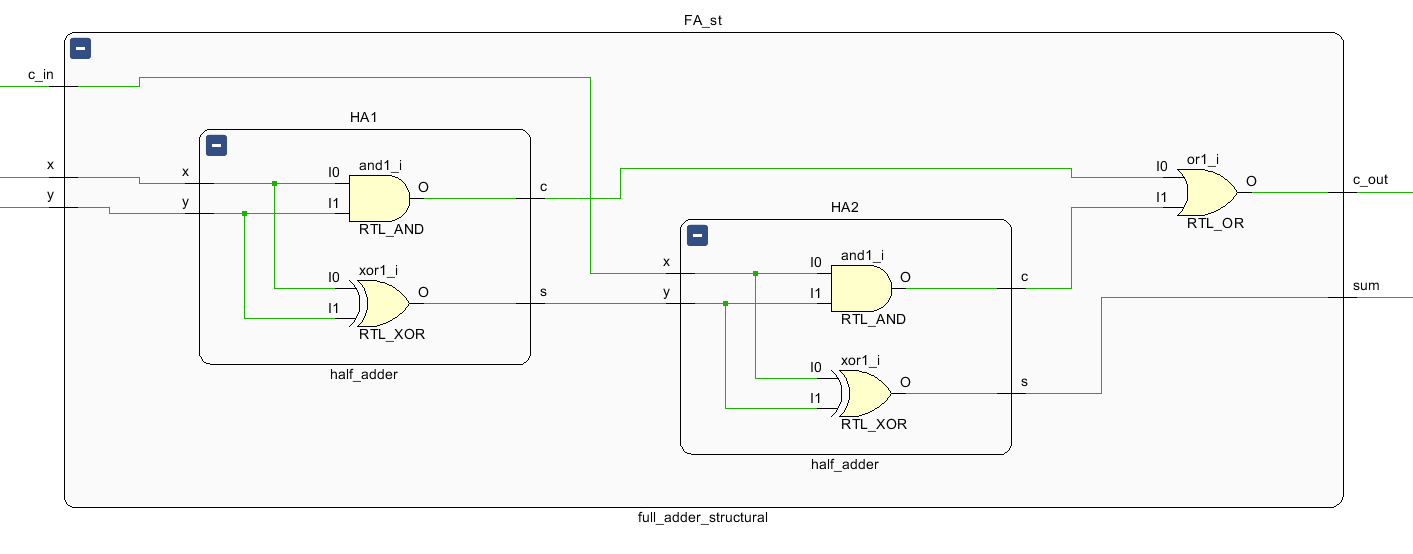
전가산기는 세 개의 1비트 이진수를 더한다. 반가산기 두 개와 OR 게이트로 구성된다.

• 첫 번째 반가산기: 입력 A와 B를 더하여 중간 합과 중간 자리올림을 생성
• 두 번째 반가산기: 첫 번째 반가산기의 합과 자리올림 입력을 더하여 최종 합과 최종 자리올림을 생성
• 최종 자리올림: 두 반가산기의 자리올림을 OR 게이트로 결합하여 생성

전가산기 진리표

입력 A	입력 B	자리올림 입력 (Carry-in)	합 (Sum)	자리올림 (Carry-out)
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

---

n비트 가산기

리플 캐리 가산기 (Ripple Carry Adder)

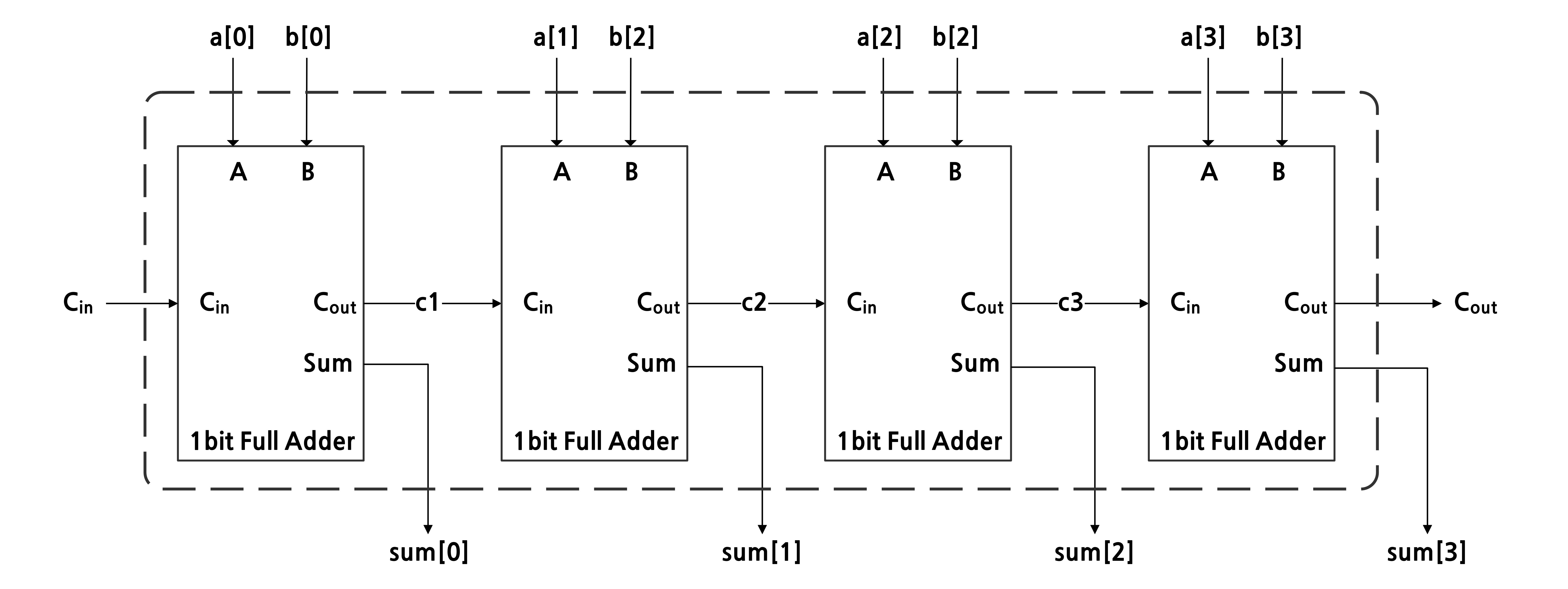
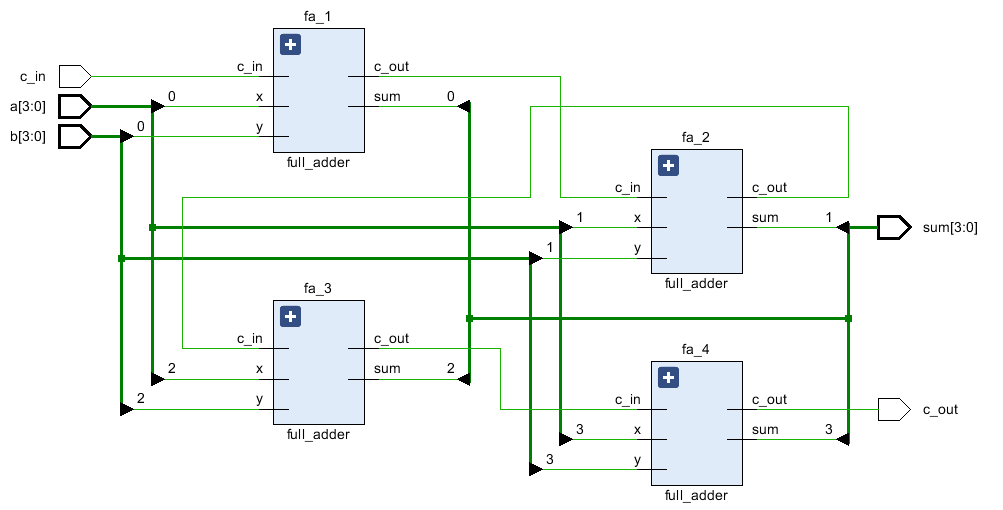
리플 캐리 가산기는 여러 개의 전가산기를 직렬로 연결하여 n비트 덧셈을 수행한다.
각 전가산기의 자리올림 출력이 다음 전가산기의 자리올림 입력으로 전달되어 최종 덧셈 결과를 얻음. 속도는 느리지만 구현이 간단하다.

---

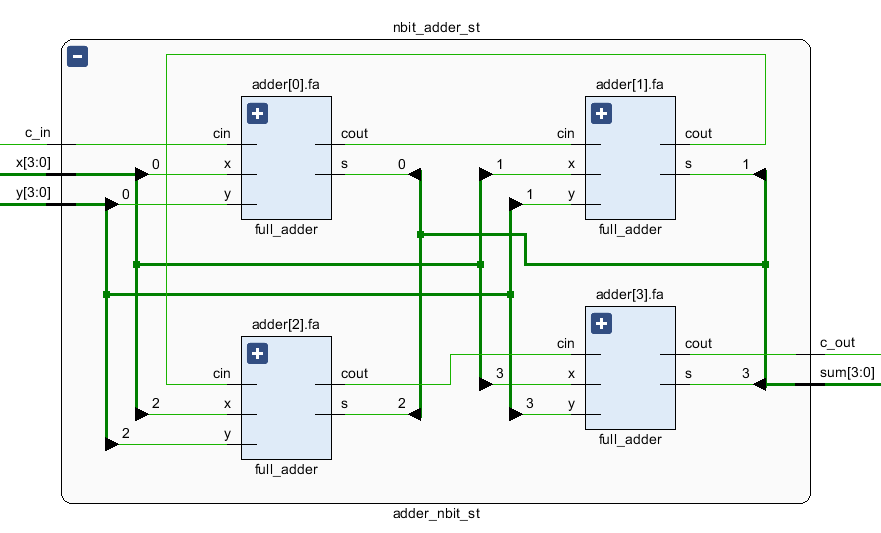
n비트 전가산기 (n bit Full Adder)

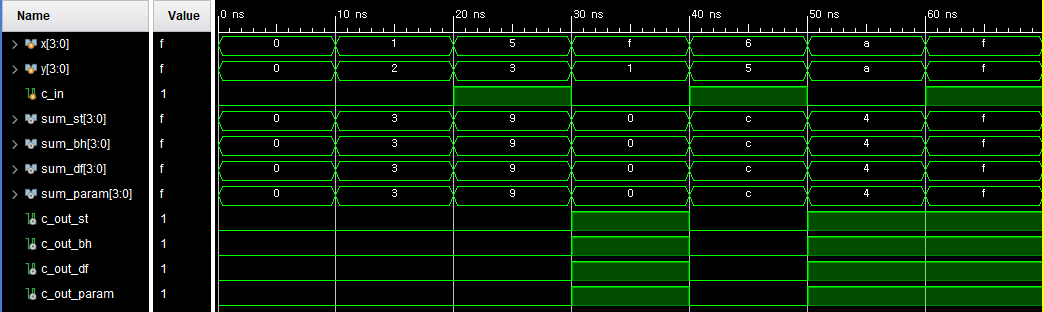
n비트 가산기는 generate문과 parameter를 이용하여 구현할 수 있다. parameter를 4로 설정했을 때 4bit adder가 구현된다.

---

ALU (Arithmetic Logic Unit)

ALU는 산술 및 논리 연산을 수행하는 컴퓨터의 핵심 장치.
덧셈, 뺄셈, 곱셈 등의 산술 연산과 AND, OR, XOR 등의 논리 연산을 수행.

Example: 4bit ALU 구현

기능
1. 덧셈
2. 뺄셈
3. AND
4. OR
5. XOR
6. NOT
7. 왼쪽 시프트
8. 오른쪽 시프트

설명

• 입력 및 출력:

  • a와 b는 4비트 입력 피연산자.
  • op_code는 수행할 연산을 선택하는 3비트 입력.
  • result는 ALU 연산의 4비트 출력.
  • carry_out은 덧셈 및 뺄셈 연산 시 발생하는 캐리 비트.

• 연산:

  • 3'b000: 덧셈
  • 3'b001: 뺄셈
  • 3'b010: AND
  • 3'b011: OR
  • 3'b100: XOR
  • 3'b101: NOT (a의 반전)
  • 3'b110: 왼쪽 시프트
  • 3'b111: 오른쪽 시프트

Carry-Lookahead Adder

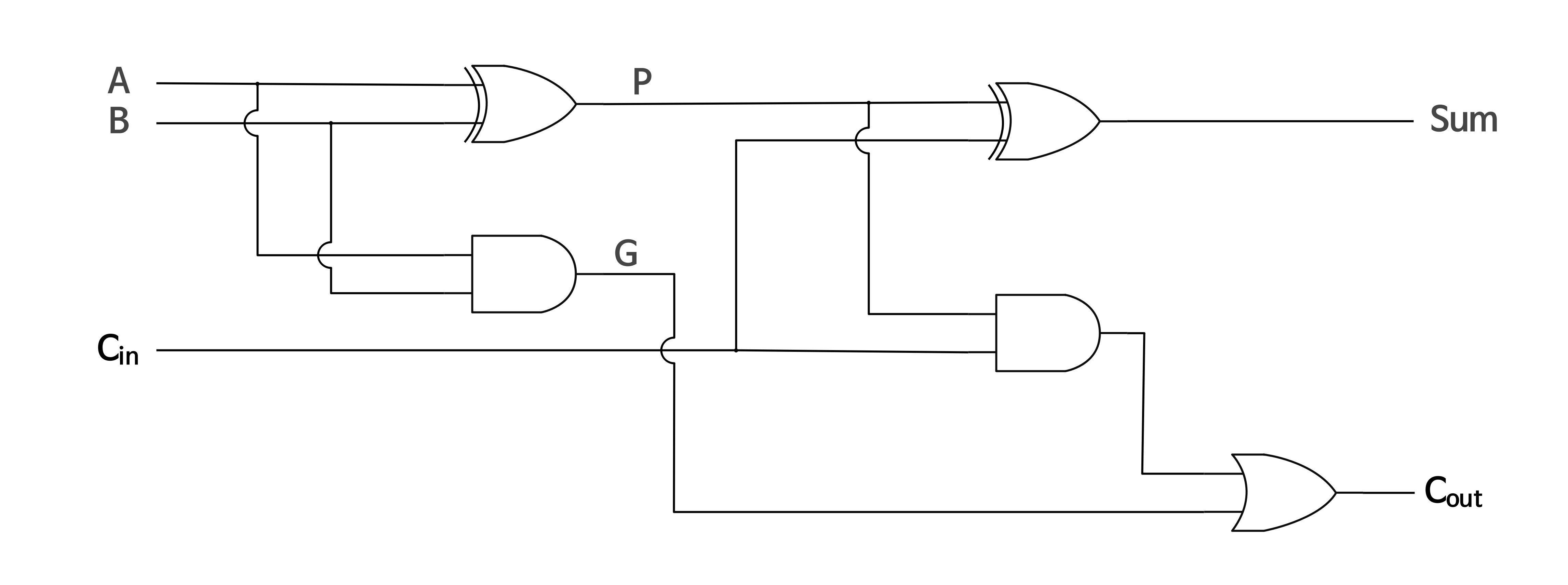
캐리 신호 계산

• Generate (G)와 Propagate (P) 신호:

  $G_i = A_i \cdot B_i$
  $P_i = A_i \oplus B_i$

• 캐리 신호 계산:

  $C_1 = G_0 + P_0 \cdot C_0$
  $C_2 = G_1 + G_0 \cdot P_1 + P_1 \cdot P_0 \cdot C_0$
  $C_3 = G_2 + G_1 \cdot P_2 + G_0 \cdot P_1 \cdot P_2 + P_2 \cdot P_1 \cdot P_0 \cdot C_0$
  $C_4 = G_3 + G_2 \cdot P_3 + G_1 \cdot P_2 \cdot P_3 + G_0 \cdot P_1 \cdot P_2 \cdot P_3 + P_3 \cdot P_2 \cdot P_1 \cdot P_0 \cdot C_0$

수식 설명

캐리 신호 계산:

• $C_1 = G_0 + P_0 \cdot C_0$

• $C_2 = G_1 + P_1 \cdot C_1 = G_1 + P_1 \cdot (G_0 + P_0 \cdot C_0)$
  $= G_1 + G_0 \cdot P_1 + P_1 \cdot P_0 \cdot C_0$

• $C_3 = G_2 + P_2 \cdot C_2 = G_2 + P_2 \cdot (G_1 + G_0 \cdot P_1 + P_1 \cdot P_0 \cdot C_0)$
  $= G_2 + G_1 \cdot P_2 + G_0 \cdot P_1 \cdot P_2 + P_2 \cdot P_1 \cdot P_0 \cdot C_0$

• $C_4 = G_3 + P_3 \cdot C_3 = G_3 + P_3 \cdot (G_2 + G_1 \cdot P_2 + G_0 \cdot P_1 \cdot P_2 + P_2 \cdot P_1 \cdot P_0 \cdot C_0)$
  $= G_3 + G_2 \cdot P_3 + G_1 \cdot P_2 \cdot P_3 + G_0 \cdot P_1 \cdot P_2 \cdot P_3 + P_3 \cdot P_2 \cdot P_1 \cdot P_0 \cdot C_0$

합 계산:

• $S_i = P_i \oplus C_{i-1}$

1. 파라미터화된 입력 및 출력:

   • N은 가변적인 비트 폭을 나타내는 파라미터.
   • A와 B는 N비트 입력.
   • Cin은 캐리 입력.
   • S는 N비트 합 출력.
   • Cout은 최종 캐리 출력.

2. 생성 및 전파 신호:

   • G는 각 비트에서의 생성 신호를 계산:
     $G[i] = A[i] \cdot B[i]$
   • P는 각 비트에서의 전파 신호를 계산:
     $P[i] = A[i] \oplus B[i]$

3. 내부 캐리 신호 계산:

   • C[0]은 초기 캐리 입력 Cin.
   • 각 내부 캐리 신호 C[i]는 생성 및 전파 신호를 이용해 미리 계산:
     $C[i] = G[i-1] \lor (P[i-1] \cdot C[i-1])$

4. 합 계산:

   • 각 비트의 합 S[i]는 전파 신호와 내부 캐리 신호를 XOR 연산하여 계산:
     $S[i] = P[i] \oplus C[i]$

5. 최종 캐리 출력:

   • 최종 캐리 출력 Cout은 내부 캐리 신호의 마지막 비트를 사용하여 계산:

     $Cout = C[N]$

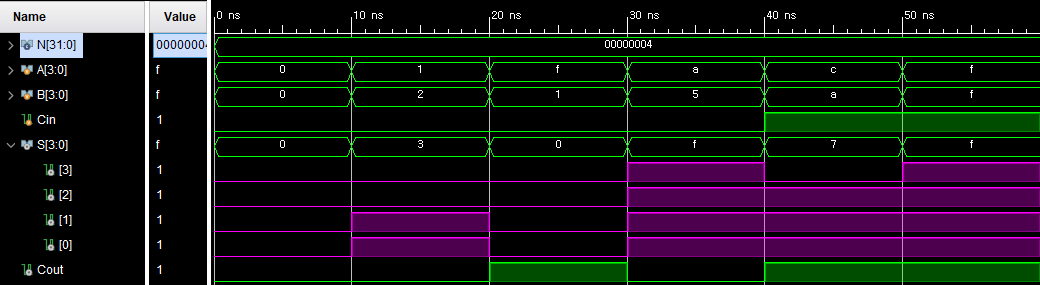
이를 바탕으로 각 비트의 합과 최종 캐리를 계산하는 Carry Lookahead Adder를 구현. 이를 통해 덧셈 속도를 향상시킬 수 있다.