선형대수학 - 벡터

Hyewon Jung·2023년 7월 15일

선형대수학

목록 보기
2/2
post-thumbnail

출처
이상엽 MATH

1. 벡터와 좌표계

1) 평면벡터

벡터 : 속도를 나타내기위해 고안된 것으로 화살표로 표시한다. 화살표의 방향은 벡터의 방향이며 길이가 벡터의 크기를 나타낸다.

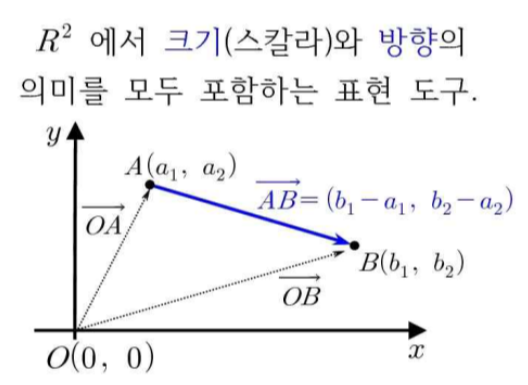
  • R2R^2 : x축, y축처럼 두개의 r, 실수축으로 만들어진 좌표평면계(2차원 평면)
  • 시점 : 벡터가 시작하는 점
  • 종점 : 벡터가 끝나는 점
B(b1,b2)B(b_1, b_2)
  • 이건 어떤 좌표평면 상의 점의 위치가 아닌 x축이 얼만큼 움직였을 때 y축으로 얼만큼 움직이는지를 나타낸 것이다.
  • 즉, 특정 좌표가 아닌 변화량이다.
  • 그러므로 좌표평면 상에 우선 표현은 해두지만 화살표가 동일한 위치, 동일한 길이라면(변화량이 같다면) 좌표평면에서 어디에 존재하든 다 똑같은 벡터로 취급한다.

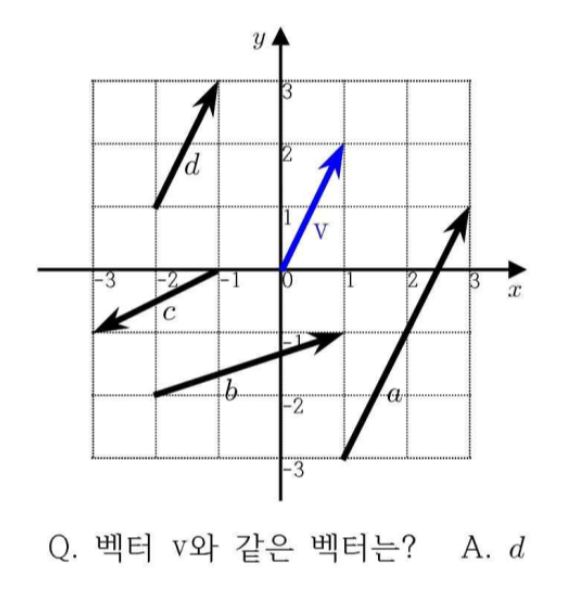
  • v와 방향이 같은 벡터 : a,d
  • v와 크기가 같은 벡터 : d,c
  • v = d
  • v(1−0,2−0)v(1-0, 2-0) = v(1,2)v(1,2)
  • d(−1−(−2),3−1)d(-1-(-2), 3-1) = d(1,2)d(1,2) -> 종점에서 시점빼준다.

2) 공간벡터

: R3R^3에서 크기와 방향의 의미를 모두 포함하는 표현 도구

  • 축이 세개

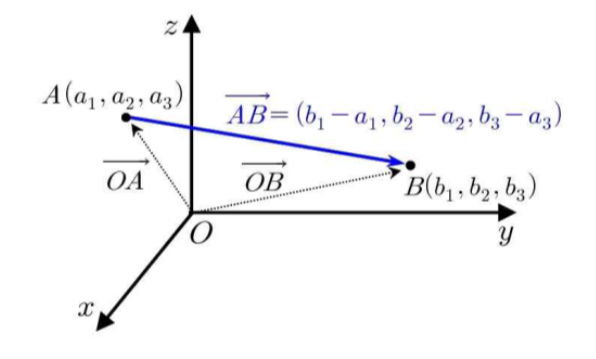
3) n차원 벡터

: RnR^n 상의 벡터 v = (v1,v2,...,vn)(v_1, v_2, ..., v_n)


  • 2차원, 3차원 등에서 원소를 3개 써줬듯이 n차원에서는 원소를 n개를 나열하면 된다.

  • AB→\overrightarrow{AB} = (b1−a1,b2−a2,....,bn−an)(b_1 - a_1, b_2 - a_2, ...., b_n - a_n)

  • 0벡터 : 0→\overrightarrow{0} = (0,0,....,0) 모든 성분이 0으로 이루어진 벡터

  • 두 벡터 v, w가 같다는 의미는 v1=w1v_1 = w_1..등 같은 자리의 원소가 동일하다는 뜻이다.




2. 벡터의 연산

1) 노름

  • 벡터의 크기(또는 길이) 라고도 한다. 유클리드 거리처럼 구해준다.
  • 벡터 화살표의 길이를 구하는 느낌이라고 생각해도 좋다.
∣∣v∣∣=v12+v22+...+vn2||v|| = \sqrt {v_1^2 + v_2^2 +...+ v_n^2}
  • 노름이 1인 벡터를 단위벡터라고 한다.
  • 정규화는 벡터의 원소를 벡터의 노름으로 나눈 것을 뜻한다.
  • 하나의 벡터만 1이고 나머지 성분이 0인 벡터를 표준단위벡터라고 한다.
  • 이때, eie_i의 i는 몇번째 원소가 1인지를 나타낸다.

    그러면 다음과 같이도 나타낼 수 있다.



2) 선형결합

(1) 벡터의 덧셈과 뺄셈

: 두 벡터 v, w가 있을 때 두 벡터를 더하고 뺀다는 것은 두 벡터의 같은 위치에 있는 원소들끼리 더하고 뺀다는 것과 같다.

v±w=(v1±w1,...,vn±wn)v\pm w = (v_1 \pm w_1 , ..., v_n \pm w_n)


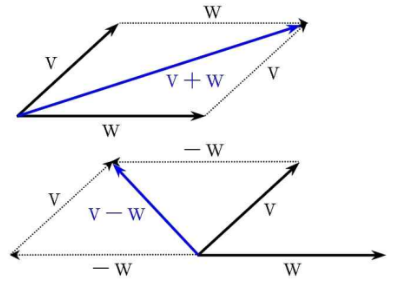
벡터의 덧셈

  • 벡터 v,w를 이용해 삼각형을 만들면 (v의 종점과 w의 시점을 연결) 밑변이 v와 w를 합친 것이 된다. (삼각형법)

벡터의 뺼셈

  • v에 -w를 더해준다고 생각하면 된다.

(2) 벡터의 실수배

: 길이를 k만큼 늘이고 줄인다고 생각하면 된다. k는 행렬의 상수배처럼 모든 원소에 적용된다.

kv=(kv1,kv2,...,kvn)kv = (kv_1, kv_2, ..., kv_n)

(3) 선형(일차) 결합

: RnR^n 의 벡터 w가 임의의 실수 (k1,k2,...,kn)(k_1, k_2, ..., k_n) 에 대하여

w=k1v1+k2v2+...+krvrw = k_1v_1+ k_2v_2 + ... + k_rv_r

의 형태(k상수배해주고 덧셈뺄셈해준)로 쓰여지면 w를 v벡터의 선형(일차)결합이라고 한다.

  • v에 대해 일차식으로 표현이 되기 때문에 일차결합이라고도 한다. v위에 지수가 존재하거나 하면 일차(선형)결합이 아니라 비선형결합이라고 한다.



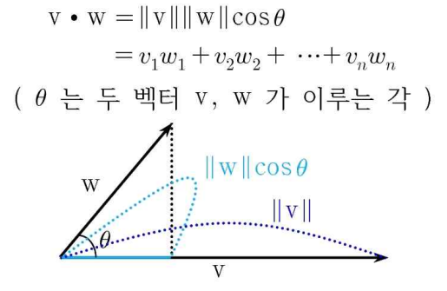
3) 스칼라곱

: 한 벡터가 다른 벡터의 방향에 대해 가한 힘에 의해 변화된 스칼라(크기) 정곱 또는 내적

  • 벡터가 크기, 방향 두가지 특성을 가지고 있기 때문에 서로다른 두 벡터에 대해 곱이 있었을 때 크기만을 반환하는 스칼라곱과 방향만을 반환하는 벡터곱 두가지를 얻을 수 있다.


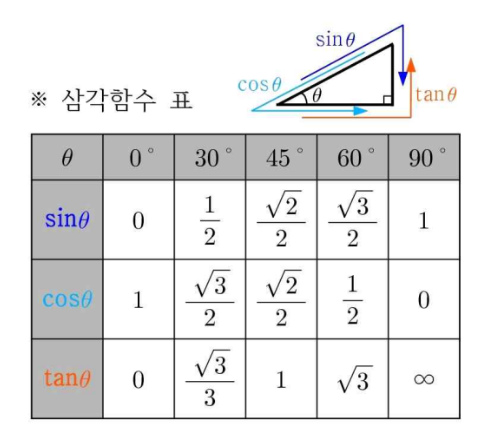
(1) 코사인표


(2) 예시

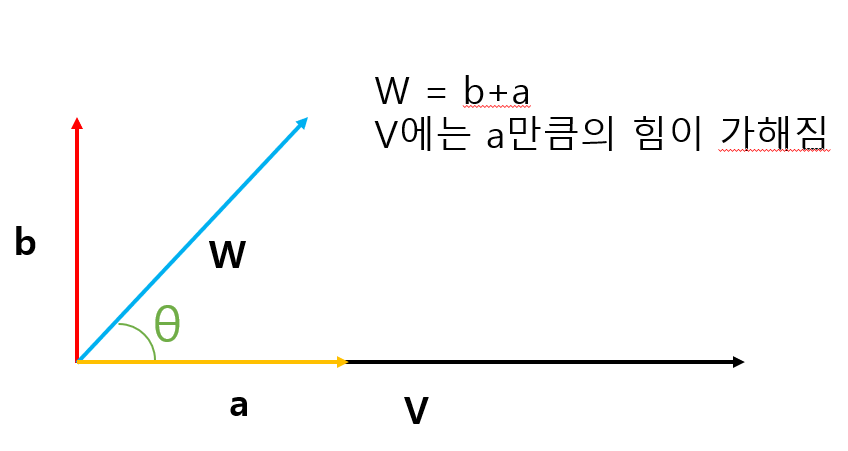
Q. ∣∣v∣∣=3||v|| = 3이고 ∣∣w∣∣=1||w||=1일 때 같은 w가 v와 같은 방향으로 힘이 작용할 때 w가 얼만큼의 힘을 가하는가?

  • 동일방향
    : 3x1 = 3
  • 방향이 같지 않을 때
    : w를 삼각형법을 이용해 구한 a와 b벡터의 합이라고 가정하면 v방향으로 a만큼의 힘을 가했다고 생각하면 된다.
    즉, ∣∣v∣∣×∣∣a∣∣||v|| \times ||a||이다. 이때, ∣∣a∣∣||a|| = ∣∣w∣∣×cosθ||w|| \times cos\theta이다.


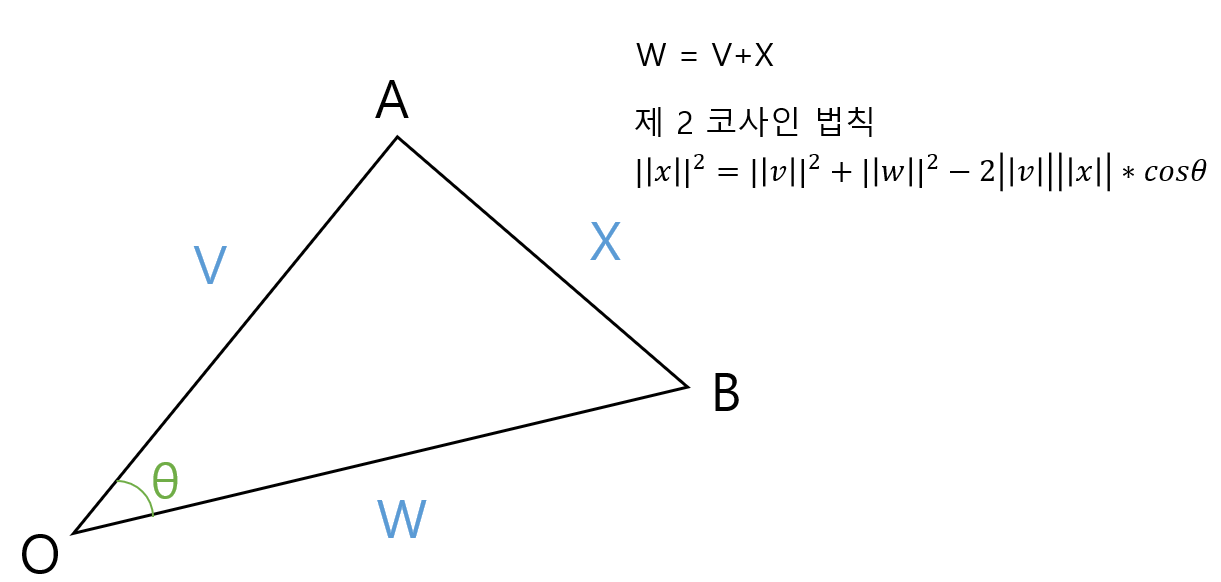
(3) 스칼라곱 증명

∣∣W−X∣∣2=∣∣v∣∣2+∣∣W∣∣2−2VM||W-X||^2 = ||v||^2 + ||W||^2 - 2VM
=VM=1/2∣∣V∣∣2+∣∣W∣∣2−∣∣W−V∣∣2= VM = 1 /2 {||V||^2 + ||W||^2 - ||W-V||^2}
12{(v12+v22...vn2)+(w12+w22...+wn2)−(w1−v1)2−...−(wn2−vn2)}\frac12 \lbrace { (v_1^2 + v_2^2 ... v_n^2) + (w_1^2 + w_2^2 ... + w_n^2) - (w_1 - v_1)^2 - ... - (w_n^2 - v_n^2)}\rbrace
=12{2w1v1+...+2wnvn}= \frac12 \lbrace {2w_1v_1 + ... + 2w_nv_n} \rbrace
=v1w1+...+vnwn= v_1w_1 + ... + v_nw_n

(4) 벡터의 연산 성질

  • 벡터의 합에서는 결합법칙이 성립한다.
  • 벡터에 0을 더해도 똑같은 벡터가 나온다. 0은 항등원이다.
  • -u는 역원으로 u와 더하면 0벡터가 나온다.
  • k와 m은 실수이다.
  • 스칼라곱에 대한 결합법칙은 성립하지 않고 의미도 없다. (스칼라곱은 스칼라(실수)가 나오기 때문에 벡터에 상수배하는 느낌이 된다.)



4) 벡터곱(가위곱, 외적)

주의점
1. 벡터곱은 R3R^3인 3차원 공간에서만 정의된다.

: 방향은 두 벡터에 동시에 수직이고, 크기는 두 벡터의 평행사변형의 면적(크기)인 R3R^3상의 벡터

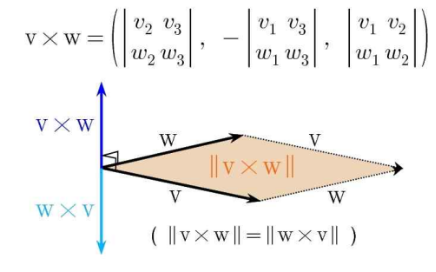
  • v와 w와 동시에 수직인 방향이 vxw이다.
  • 방향은 v와 w중 뭐가 앞에 오느냐에 따라 다르다.(곱하는 순서에 따라 다르다.) v가 앞에 오면 그림과 같이 위로, w가 앞에 오면 아래로 향한다.

(1) 예시

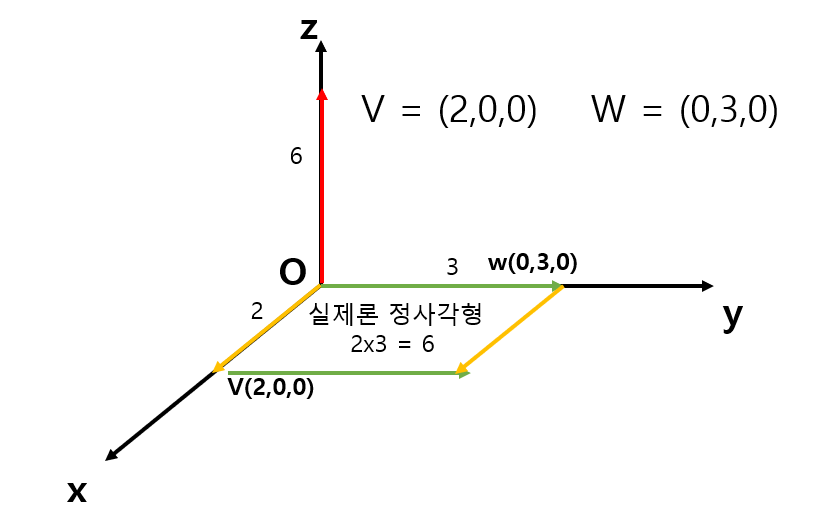
VM={(v2w3−w2v3),−(v1v3−v3w1),(v1w2−w1v2)}=(0,0,6)VM = \lbrace (v_2w_3 - w_2v_3) ,- (v_1v_3 - v_3w_1) , (v_1w_2 - w_1v_2) \rbrace = (0,0,6)
  • VM은 공동으로 수직인 방향으로 평행사변형의 면적만큼의 길이를 가지게 된다.

(2) 벡터 곱의 성질

  • 동일한 벡터를 곱해주면 0벡터가 나온다. 동일한 벡터를 가지고 평행사변형을 만들 수 없기 때문이다.
  • 교환법칙, 결합법칙 둘 다 성립하지 않는다.



3. 벡터의 응용

1) 직선의 표현

: R2R^2 또는 R3R^3에서 위치벡터 (원점을 시점으로하는 벡터) 가 a인 점 A를 지나며 방향벡터 (직선이 늘어나는 방향을 지시하는 벡터) 가 v인 직선상의 임의의 점 X의 위치벡터 x는

x=a+kwx = a + kw

을 만족한다. (단, k는 임의의 실수)

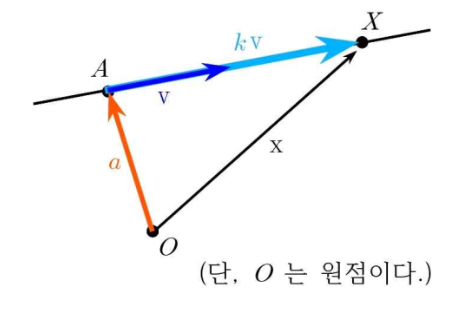
(1) 예시



2) 평면의 표현

: R3R^3에서 위치벡터 (원점을 시점으로하는 벡터) 가 a인 점 A를 지나며 법선벡터 (평면에 수직인 벡터, 아래그림에서 하늘색선) 가 v인 평면상의 임의의 점 X의 위치벡터 x는 다음식을 만족한다.

  • 법선 벡터 = 평면상의 서로 다른 두 직선의 방향벡터들의 벡터곱으로 구한다.
(x−a)V=0(x-a)V = 0

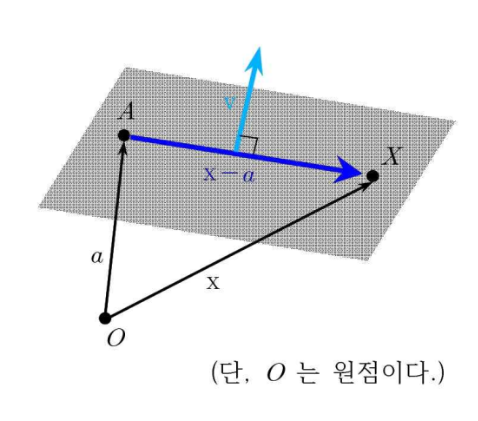
  • 남색선 : x-a (삼각형법)
  • 하늘색선(V) : 평면에 수직 -> 노란선과도 수직 -> cos90도(=0) -> 따라서 스칼라 0

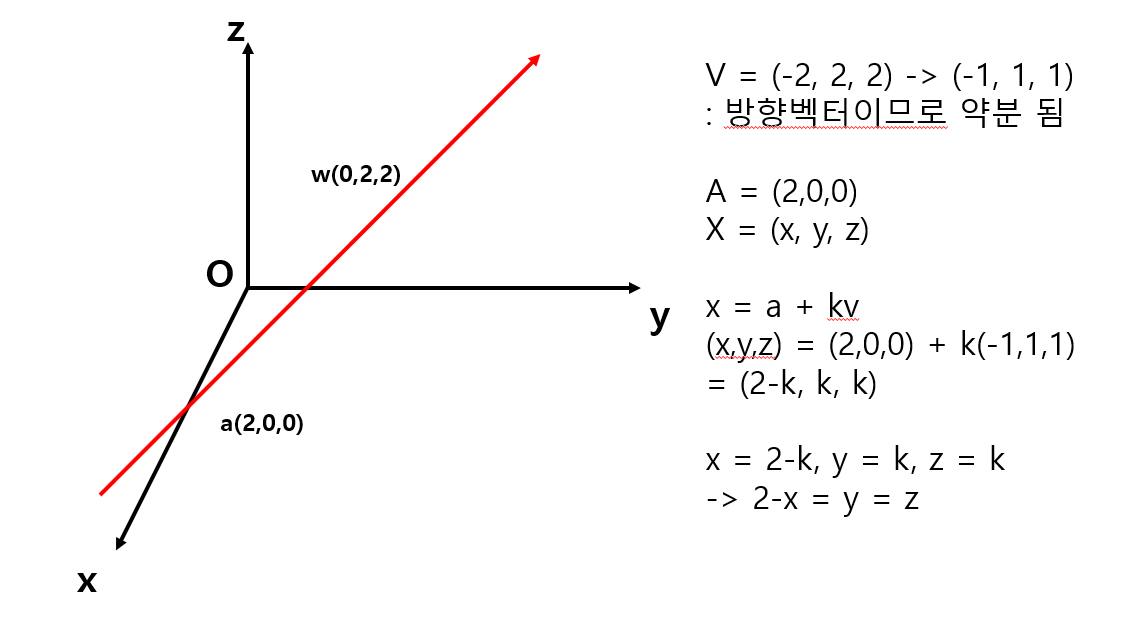
(1) 예시

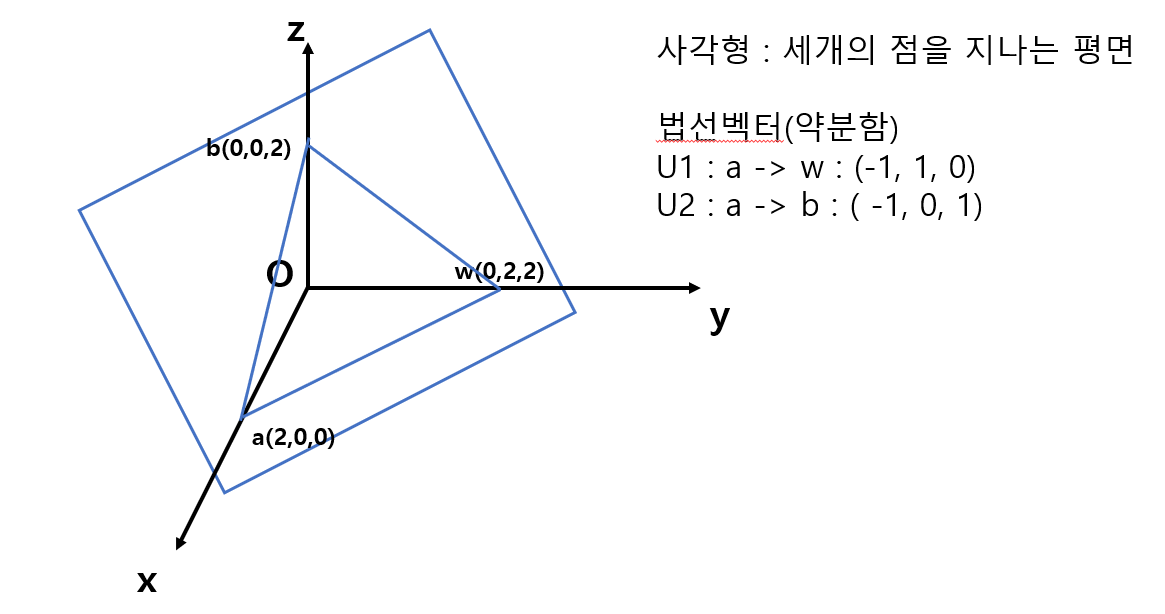
  • 벡터곱

    VM=u1u2={(v2w3−w2v3),−(v1v3−v3w1),(v1w2−w1v2)}=(1,1,1)VM = u_1u_2 = \lbrace (v_2w_3 - w_2v_3) , - (v_1v_3 - v_3w_1) , (v_1w_2 - w_1v_2) \rbrace = (1,1,1)

  • 위치벡터 x 구하기

x=(x,y,z)x = (x,y,z)
a=(2,0,0)a = (2,0,0)
(x−a)V=0(x-a)V = 0

(x−2,y,z)(1,1,1)=x−2+y+z=0(x-2,y,z)(1,1,1) = x-2+y+z = 0

-> 이 식을 평면의 방정식이라고 한다.

profile
Hyewon Jung
Amateur data scientist & student
이전 포스트

선형대수학 - 행렬과 행렬식

0개의 댓글