[BOJ] 4195번 - 친구 네트워크

프로그래머스 알고리즘 고득점 kit 해시 파트를 풀고 나서 백준으로 넘어와서 풀어보고 있는데 이 문제에서 막혔다;;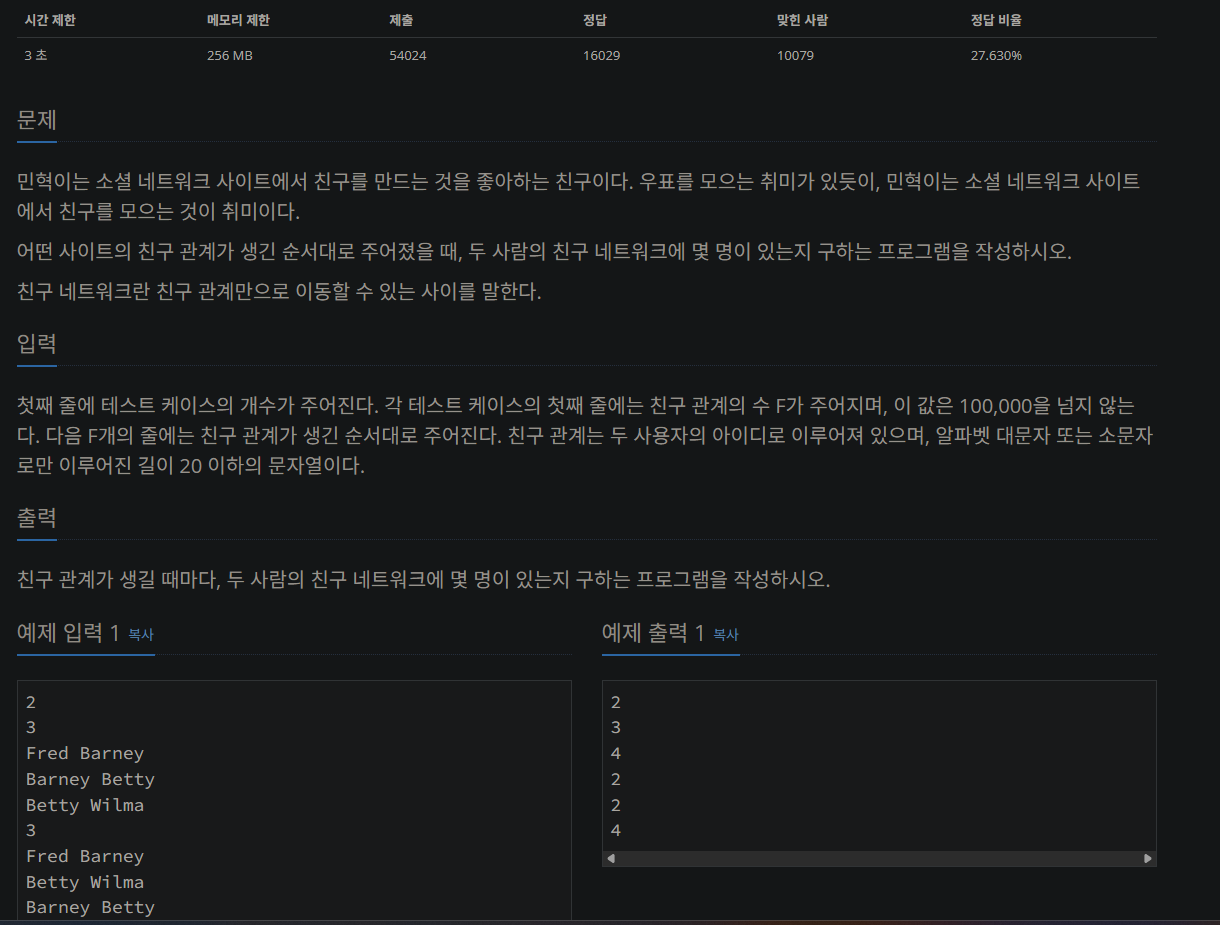

첫 풀이

내 첫 풀이는 다음과 같았다.

import sys
input = sys.stdin.readline
T = int(input())
for _ in range(T):
  F = int(input())
  dic = {}
  for _ in range(F):
    arr = input().split()
    if (arr[0] not in dic) and (arr[1] not in dic):
      dic[arr[0]] = 1
      dic[arr[1]] = 1
      print(2)
    else:
      if arr[0] in dic:
        dic[arr[0]] += 1
      else:
        dic[arr[0]] = 1
        dic[arr[1]] += 1
      print(len(dic.keys()))

결과는
ㅋ~.

생각해보니까 예시말고도
이런 경우가 있었다.

# 입력
1
5
Fred Barney
Barney Betty
Wilma Shelley
Shelley Dorothy
Dorothy Betty

# 출력
2
3
2
3
6

이렇게 두 개의 집합이 생겼다가 마지막에 두 집합을 묶어지는 하는 경우..

풀이를 찾아보니까, union, find 함수를 만들어서 풀더라..

이게 뭔소린가 싶었는데 union-find 알고리즘이라는 게 있었다.
이 개념에 대한 이해와 활용이 필요할 것 같아 찾아보고 정리해보았다.

Union-Find 알고리즘

출처: https://chiefcoder.tistory.com/55

💡 유니온 파인드란?

• 유니온 파인드는 그래프 알고리즘으로 두 노드가 같은 그래프에 속하는지 판별하는 알고리즘이다
• 노드를 합치는 Union 연산과 노드의 루트 노드를 찾는 Find 연산으로 이루어진다

아 이거 분명히 컴알 수업 때 들었을 건데;; 열심히 들을걸ㅠ

8개의 노드들(단절된, 아직 연결x)
이 노드들은 배열에 자기 자신의 값을 가지고 있음

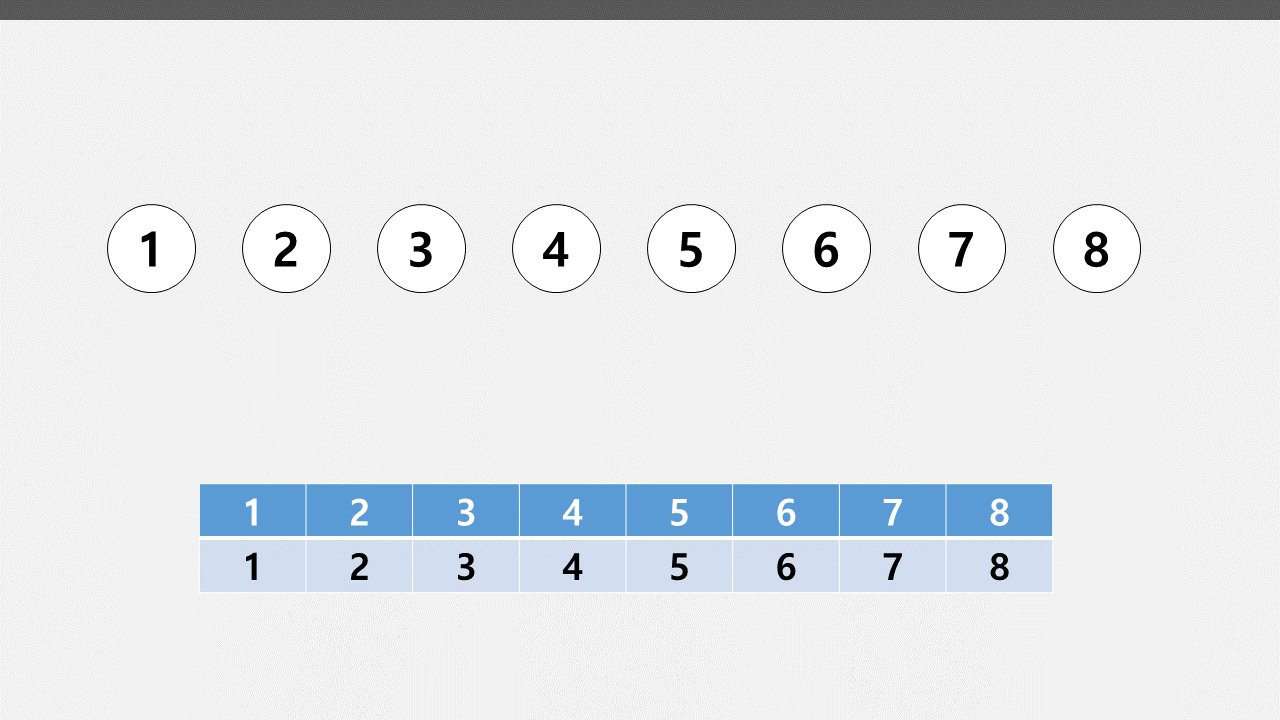
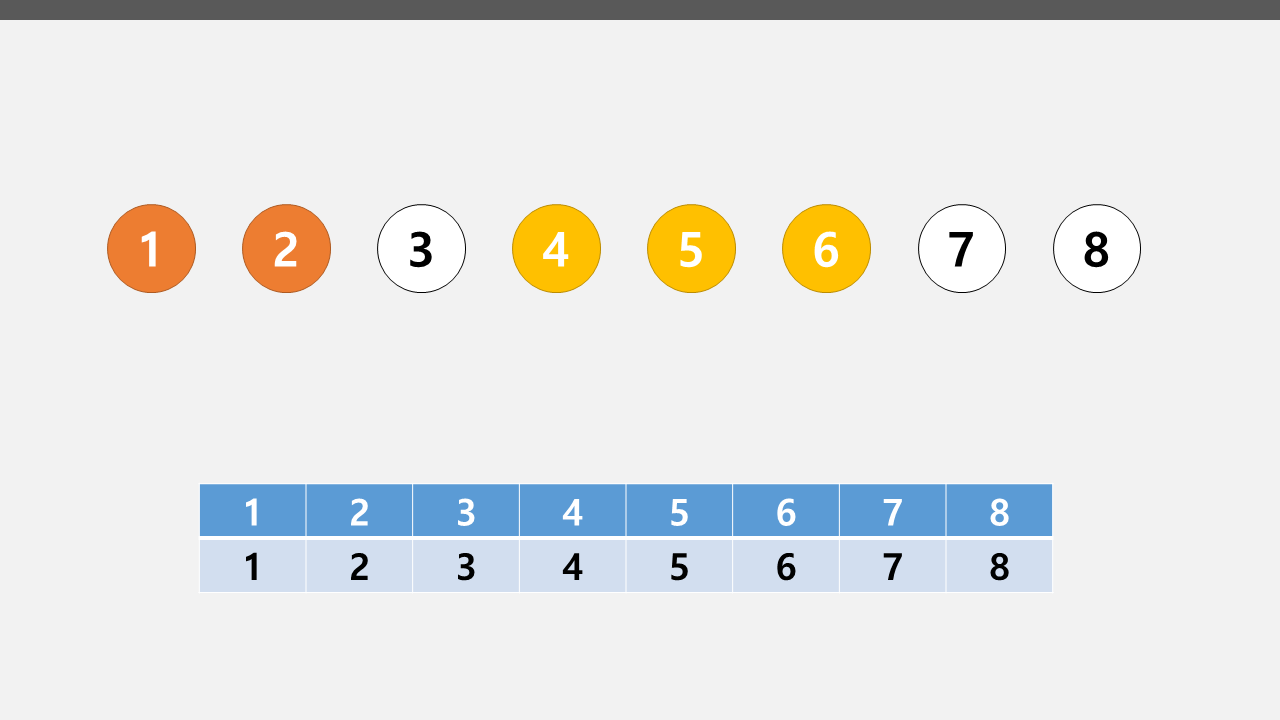이 중 1 2 노드를 연결하고 4 5 6 노드들을 연결하고 싶다고 가정해보자.
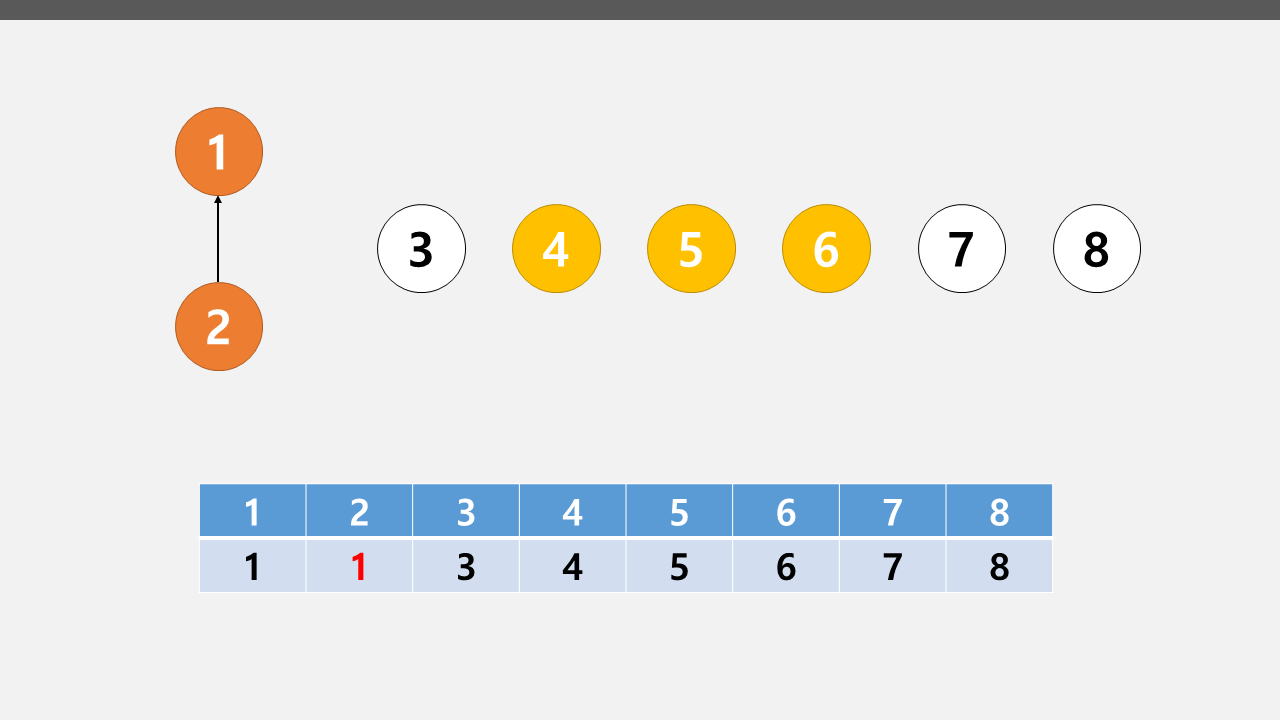우선 1 2 노드를 합쳐본다.
합치는 방법은 간단하다. 2번 노드의 배열 값을 1번 노드의 배열 값으로 바꿔주면 된다.

4 5 6도 마찬가지로 바꿔보자.
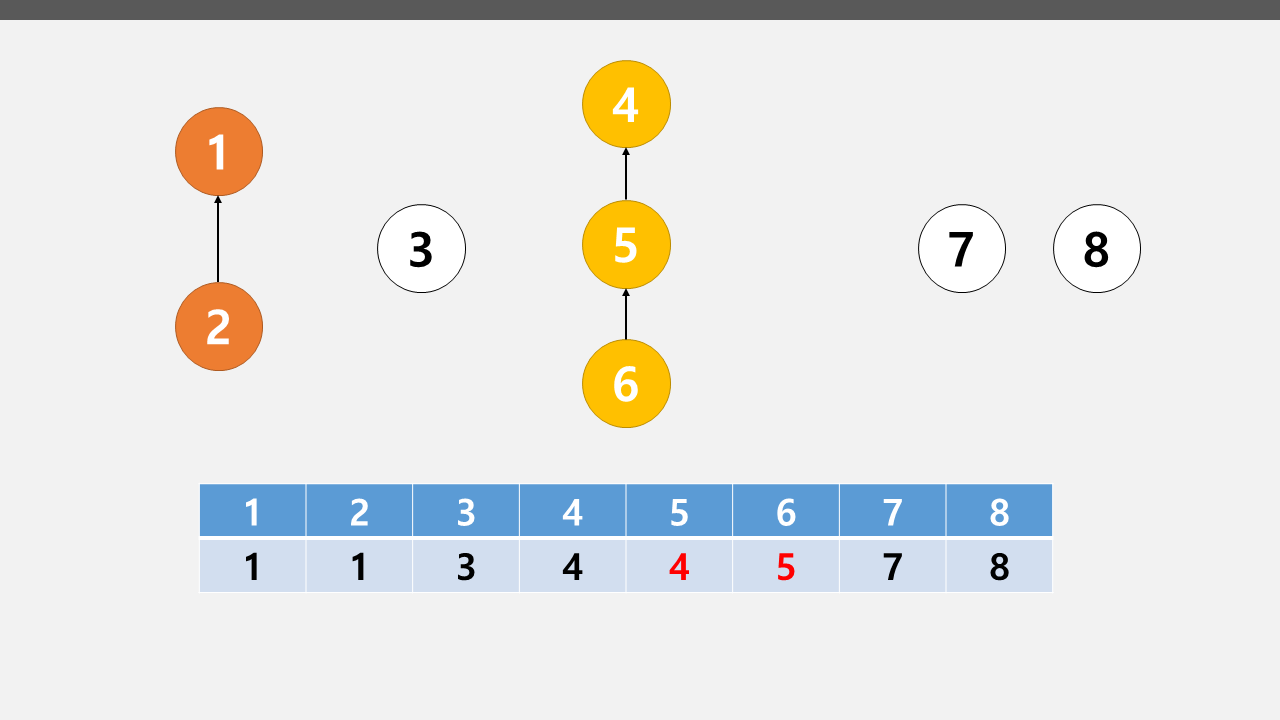4와 5를 연결하고 5와 6을 연결하면 그림처럼 배열이 바뀐다. 이제 어떻게 노드들이 연결되어 있는지 아닌지 판별할 수 있는지 감이 오실거다.
예를 들어 2번과6번 노드가 연결되어 있는지 확인하고 싶다면

• 2번 노드의 부모를 찾는 과정
  1. 배열의 2번에 있는 값을 확인합니다 => 1번 이다.
  2. 배열의 1번에 있는 값을 확인합니다 => 1번 이다.
  3. 배열의 인덱스와 값이 일치합니다.
  4. 그렇다면 1번 노드가 2번 노드가 속해있는 트리의 루트 노드이다.
• 6번 노드의 부모를 찾는 과정
  1. 배열의 6번에 있는 값을 확인합니다. => 5번 이다.
  2. 배열의 5번에 있는 값을 확인합니다. => 4번 이다.
  3. 배열의 4번에 있는 값을 확인합니다. => 4번 이다.
  4. 배열의 인덱스와 값이 일치한다.
  5. 4번 노드가 6번 노드가 속해있는 트리의 루트 노드이다.

이제 각각 노드의 루트 노드를 비교해서 서로 다르다면 두 노드는 연결되어 있지 않은 것이다.
하지만 이렇게만 바꾸면 문제가 발생한다.

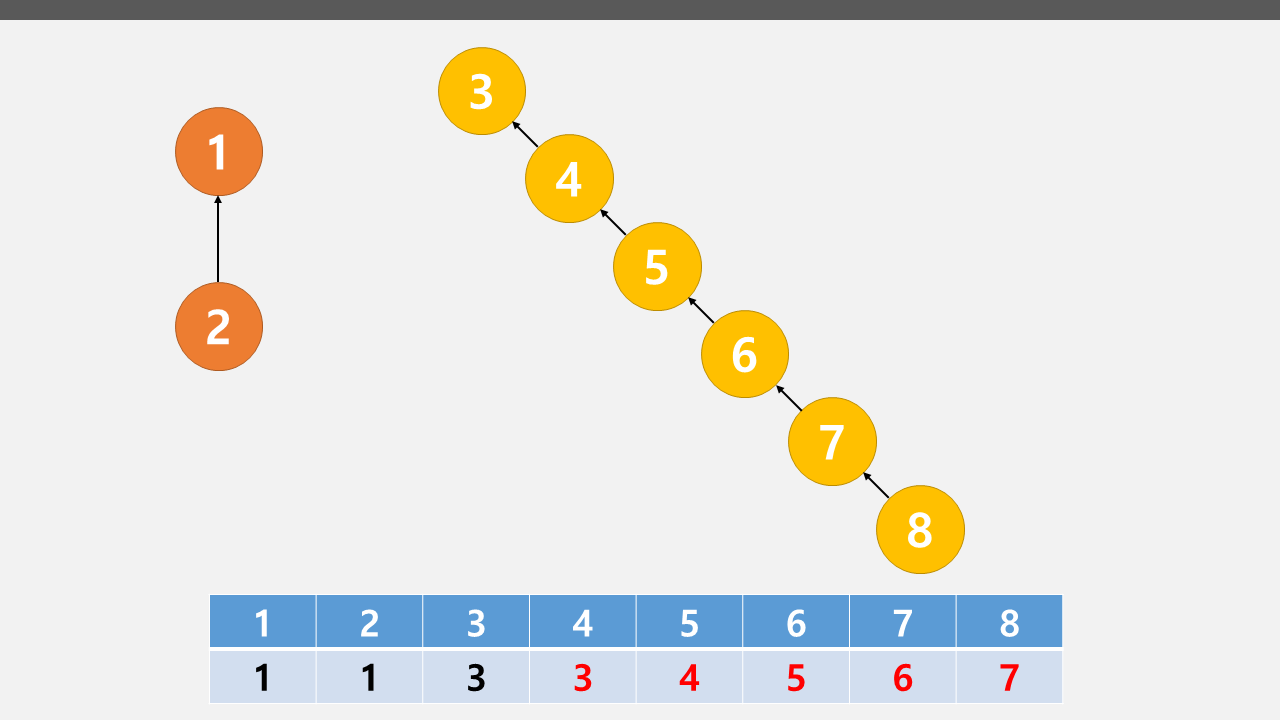
위의 예처럼 트리의 문제 중 하나인 한쪽으로만 자식이 몰려있는 편중현상이 생길 수 있다.

Find연산에서 재귀를 통해 루트 노드를 찾아야하는데 이렇게 편중되어 있으면 탐색하는데 시간이 많이 걸린다.

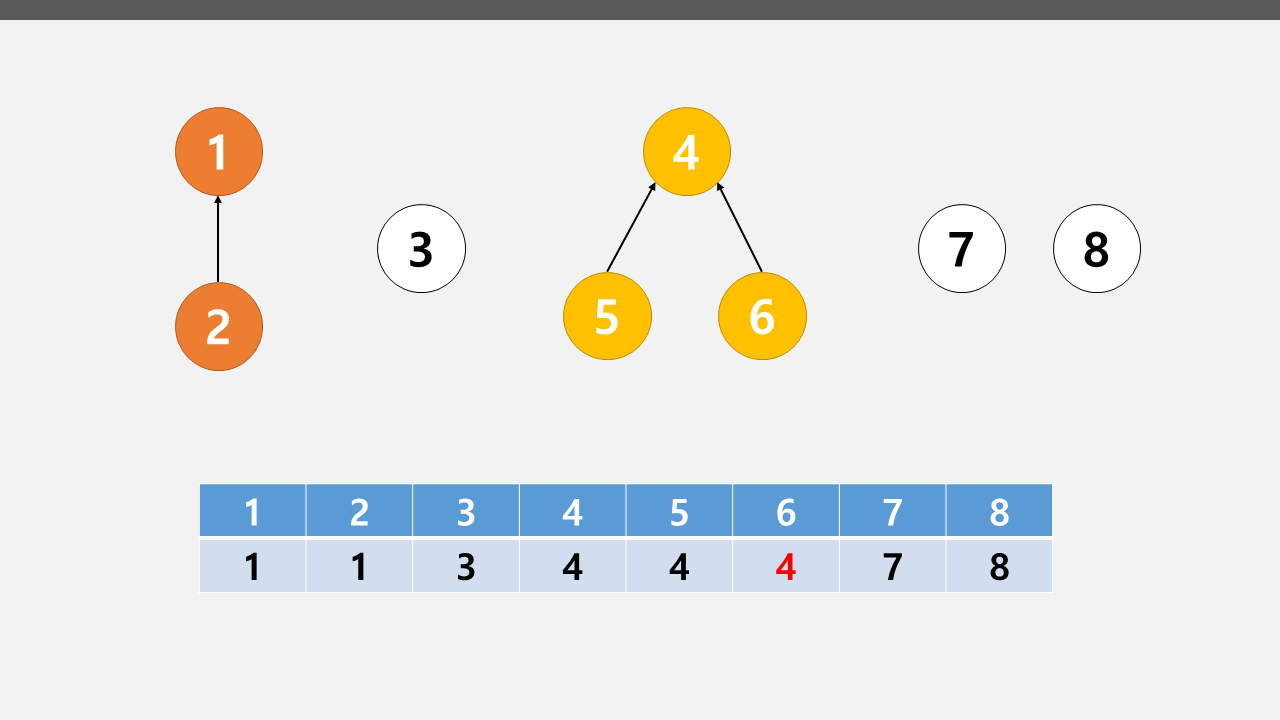
위의 편중 문제를 해결하기 위해 합치는 Union 연산을 할 때
루트 노드를 찾는 탐색 과정을 통해 루트노드에 연결하는 과정을 거쳐
결과적으로 위의 그림처럼 트리가 형성된다.

1 2를 연결하고 4 5 6을 연결한 유니온 파인드의 트리구조이다.

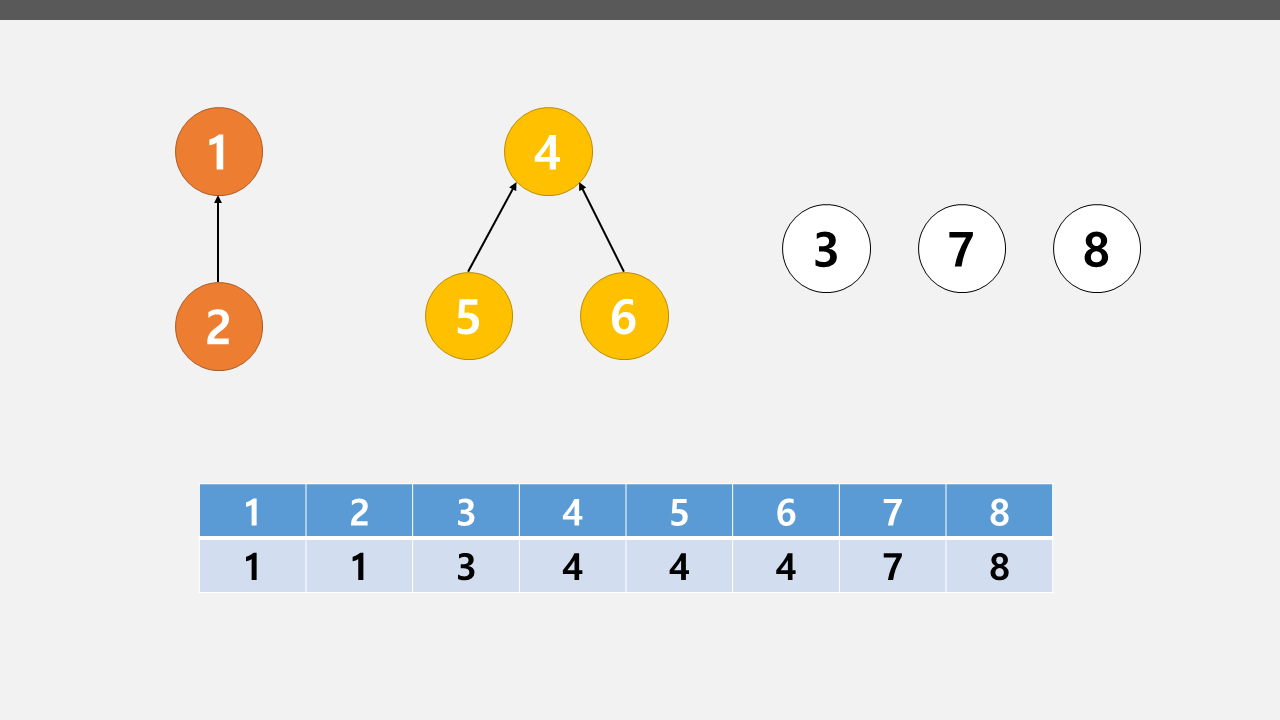
이제 1과 4번 노드를 연결하고 싶다면 아래 그림처럼 바뀔 것이다.

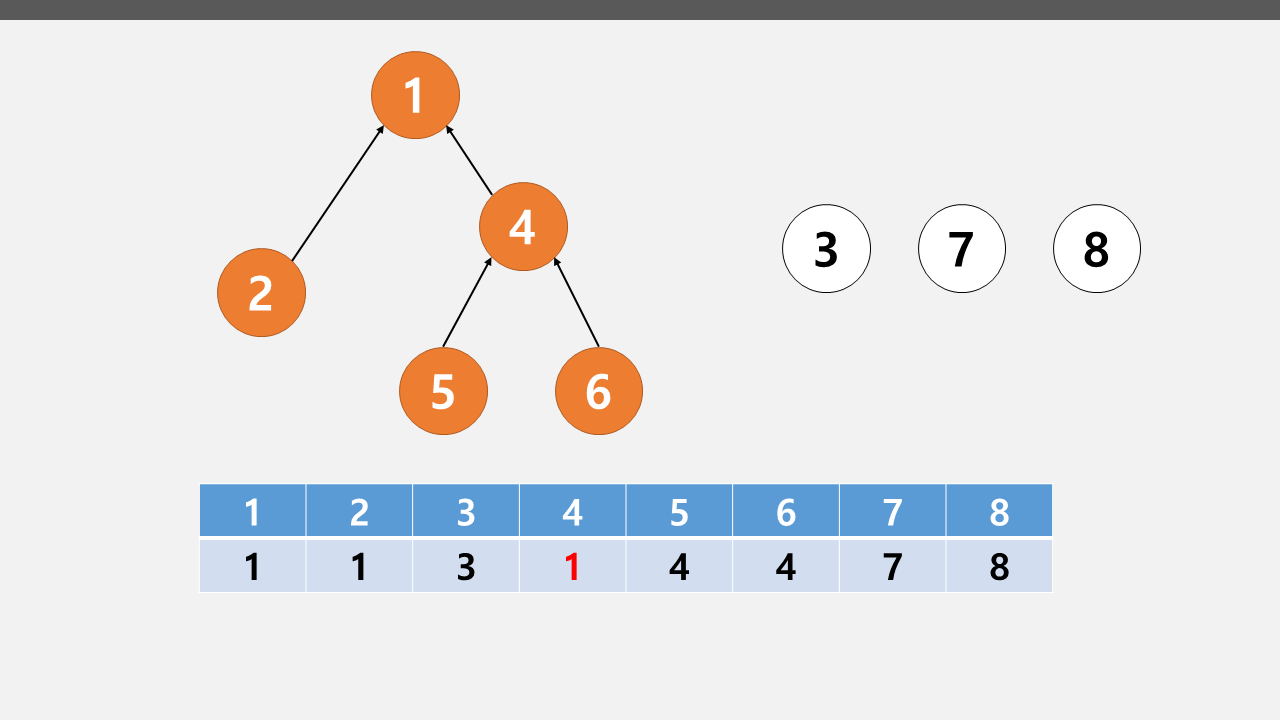
Python에서의 유니온 파인드 구현

출처: https://chiefcoder.tistory.com/55

# 특정 원소가 속한 집합을 찾기
def find(x):
	# 루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
    if parent[x] != x:
    	return find(parent[x])
    return x

# 두 원소가 속한 집합을 합치기
def union(a, b):
	 a = find(a)
     b = find(b)
     if a < b:
     	parent[b] = a
     else:
     	parent[a] = b

# 노드의 개수와 간선(Union 연산)의 개수 입력 받기
v, e = map(int, input().split())
parent = [0]* (v + 1) # 부모 테이블 초기화하기

# 부모 테이블상에서, 부모를 자기 자신으로 초기화
for i in range(1, v + 1):
	parent[i] = i

# Union 연산을 각각 수행
for i in range(e):
	a, b = map(int, input().split())
    union(a, b)

# 각 원소가 속한 집합 출력하기
print('각 원소가 속한 집합: ', end='')
for i in range(1, v + 1):
	print(find(i), end=' ')

print()

# 부모 테이블 내용 출력하기
print('부모 테이블: ', end='')
for i in range(1, v + 1)
	print(parent[i], end=' ')

find 함수 부분을 '경로 압축'(Path Compression)을 통해 다음과 같이 리팩토링할 수 있다.
시간 복잡도가 감소하므로 이 코드를 사용하는 것이 좋다.

def find_parent(x):
	# 루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
    if parent[x] != x:
    	parent[x] = find_parent(parent[x])
    retrun parent[x]

다음은 다른 블로그에서 union-find 알고리즘을 설명한 것이다.

출처: [알고리즘] union-find 알고리즘

수학에서의 서로소 집합

공통 원소가 없는 두 집합
e.g. {1,2} {3,4} -> 서로소 관계임 {1,2} {2,3} -> 서로소 관계가 아님

서로소 집합 자료구조

서로소 부분 집합들로 나누어진 원소들의 데이터를 처리하기 위한 자료구조
-> 연산 : union + find

union
2개 원소로 이루어진 집합을 하나의 집합으로 합치기

find
특정 원소가 속한 집합이 뭔지 알려주는 연산
-> 서로소 집합 자료구조는 union + find 연산으로 구성되므로 union-find 자료구조라고 불리기도 함

서로소 집합 계산 알고리즘 동작 방법

1. union 연산 확인
   : 서로 연결된 두 노드를 확인
   1.1 A의 루트 노드 A'과 B의 루트 노드 B'를 찾기 (find)
   1.2 A'를 B'의 부모 노드로 설정 (A' < B')
2. 모든 union 연산을 처리할 때까지 1 반복

e.g.
{1,2,3,4,5,6}의 집합과 4개의 union 연산 union 1,4 union 2,3 union 2,4 union 5,6이 주어졌다.
이를 그래프로 표현하면,

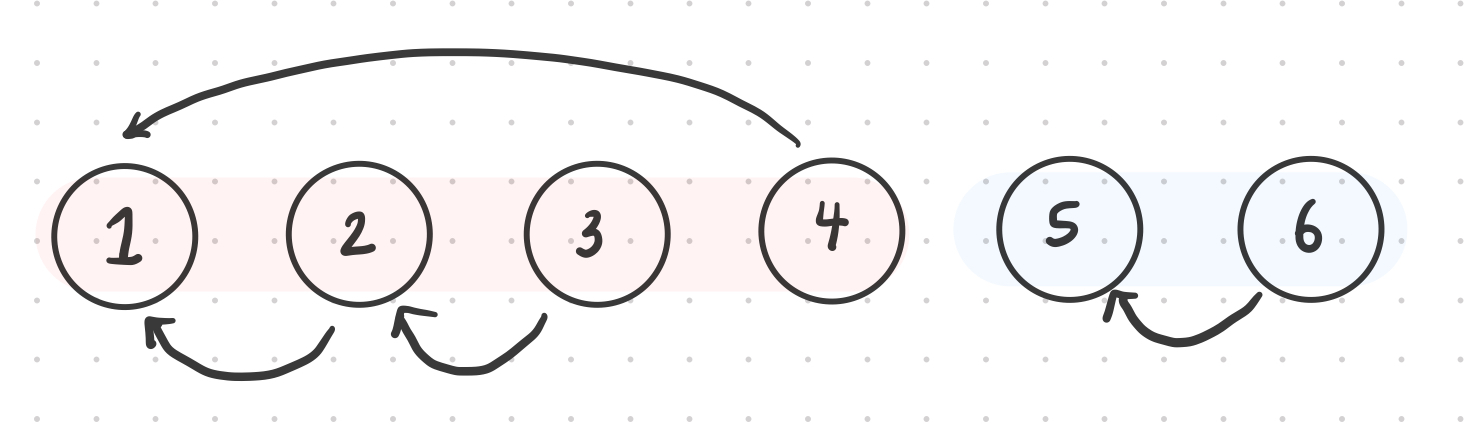
위와 같이 구성됨을 알 수 있다.
이를 완성하기 위한 구체적인 알고리즘 동작 방법은 아래와 같다.

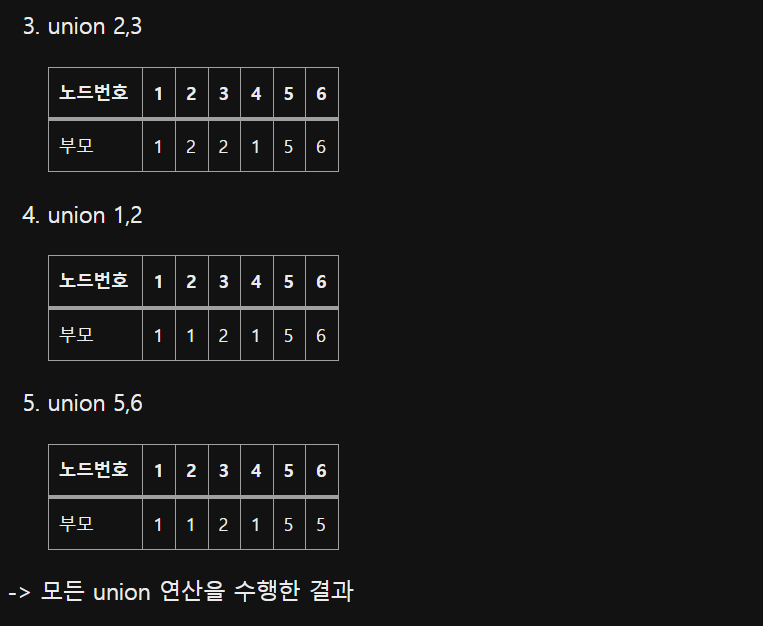
[BOJ] 4195번 파이썬 풀이

import sys
input = sys.stdin.readline

def find(x): # x 노드의 루트 노드를 찾는 함수
    if parent[x] == x: # x 노드가 루트 노트라면 x 반환
    	return x
    else:
        p = find(parent[x]) # x의 부모 노드의 루트 노드 찾기
        parent[x] = p
        return p

def union(x, y):
    x, y = find(x), find(y) # 서로 연결된 두 노드 x,y의 루트 노트 반환

    if x != y: # 만약 두 루트 노드가 다르다면, 루트 노드 연결
        parent[y] = x # y의 부모 노드는 x의 루트노드
        number[x] += number[y] # x 집합에 y 집합 수 연결
    print(number[x])

T = int(input())
for _ in range(T):
    F = int(input())
    parent, number = {}, {}
    for i in range(F):
        a, b = input().split()
        if a not in parent:
            parent[a] = a
            number[a] = 1
        if b not in parent:
            parent[b] = b
            number[b] = 1
        union(a, b)

• 일반적인 유니온 파인드와 다르게 숫자가 아닌 문자열이 들어가므로 친구의 숫자를 저장하기 위한 리스트를 하나 더 선언해주어야하는 문제였다
• 나머지는 유니온 파인드와 동일하게 문제를 해결할 수 있다
  • find 함수: 특정 노드가 속한 집합(루트 노드)를 찾는 함수
  • union 함수: 서로 연결된 두 노드의 루트 노드를 연결하는 함수

앞으로 다른 문제들도 풀어보면서 유니온-파인드 알고리즘을 익혀보도록 하겠다~~🖐️