코테를 앞두고 있어 알고리즘별 기본 문제들을 모두 복기해보았습니다.
1. 완전 탐색
1.1 백트래킹
백트래킹은 알고리즘 기법 중 하나로, 재귀적으로 문제를 하나씩 풀어가면서 현재 재귀를 통해 확인 중인 노드(상태)가 제한된 조건에 위배되는지 판단하고, 만약 해당 노드가 "제한된 조건을 위배한다면 그 노드를 제외" 하고 다음 단계로 나아가는 방식이다.
백트래킹은 현재 상태에서 다음상태로 가는 모든 경우의 수를 찾아서 이 모든 경우의수가 더 이상 유망하지 않다고 판단되면 이전의 상태로 돌아가는 것을 말한다.
여기서 더 이상 탐색할 필요가 없는 상태를 제외하는 것을 가지치기(pruning)라고도 한다.
따라서 한마디로 정의하면 DFS를 통해 모든 노드를 깊이 우선 탐색을 하면서 더 이상 필요가 없는 부분을 쳐내는 행위를 백트래킹(가지치기) 이라고 생각하면된다.
백트래킹 문제 중 가장 대표적인 문제인 N-Queen 문제를 풀어보겠다.
✅ 문제
https://www.acmicpc.net/problem/9663
✅ 풀이
import sys
input = sys.stdin.readline
def dfs(n):
global ans
if n == N: # N행까지 진행한 경우 경우의 수 가능: 성공
ans += 1
return
for j in range(N):
if v1[j]==v2[n+j]==v3[n-j]==0: # 열/대각선 모두 Q 없음
v1[j] = v2[n+j] = v3[n-j] = 1
dfs(n+1)
v1[j] = v2[n+j] = v3[n-j] = 0
N = int(input())
ans = 0
v1 = [0]*N
v2 = [0]*(2*N)
v3 = [0]*(2*N)
dfs(0)
print(ans)참고: [백준 문제집] 백트래킹
백트래킹은 가능한 모든 조합에 대해 전부 시도를 하는 것이다. '가능한 모든 조합'이기 때문에 조건에 맞을 경우에 전부 시도를 한다.
"DFS with promising function": 단순히 DFS와 BFS를 위한 문제를 풀 때는 그래프 모양만 생각하면 되지만 백트래킹에서는 트리모양을 생각하면 좀 더 이해하기가 쉽다. promising function에서 promising은 tree에서 특정 node를 방문할 것인지 아닌지를 판단하는 것으로, 해당 조합이 가능한 경우인지를 판단하는 것이다.
1.2 DFS, BFS
DFS는 깊이 우선 탐색으로, 현재 정점에서 갈 수 있는 점들까지 들어가면서 탐색하는 방법이다. 탐색 트리의 최근에 첨가된 노드를 선택하고, 해당 노드의 끝까지 탐색하고 목표 노드에 도달하면 멈추고 아니면 그 다음 노드의 자식노드들을 또 끝까지 탐색한다. 스택 또는 재귀함수로 구현한다.
BFS는 너비 우선 탐색으로, 현재 정점에 연결된 가까운 점들부터 탐색하는 방법이다. 더 이상 방문하지 않은 정점이 없을 때까지 방문하지 않은 모든 정점들에 대해서도 너비 우선 검색을 적용한다. 큐를 이용해서 구현한다.
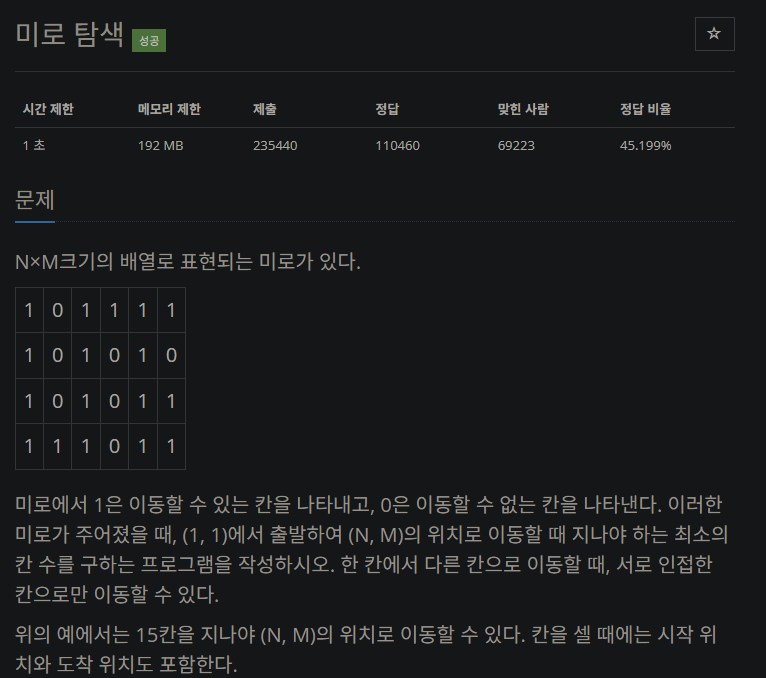
✅ 문제
https://www.acmicpc.net/problem/2178
✅ 풀이
from collections import deque
import sys
input = sys.stdin.readline
N, M = map(int, input().split())
graph = [list(map(int, ' '.join(input().split()))) for _ in range(N)]
queue = deque([(0,0)])
dx = [0, 0, 1, -1]
dy = [1, -1, 0, 0]
cnt = 0
while queue:
x, y = queue.popleft()
for i in range(4):
next_x, next_y = x+dx[i], y+dy[i]
if 0 <= next_x < N and 0<=next_y<M:
if graph[next_x][next_y] == 1:
queue.append((next_x, next_y))
graph[next_x][next_y] = graph[x][y] + 1
print(graph[N-1][M-1])이 문제는 BFS로 풀어야 한다. 그 이유는 DFS로는 처음에 운 좋으면 찾을 수 있지만 운이 않좋으면 모든 최장거리도 가능하기 때무에 최단거리를 찾는 문제에서는 유리하지 않다.
파이썬은 따로 queue를 구현한 자료구조가 없기 때문에 deque를 통해서 queue 자료구조의 동작을 구현해주면 된다. 만약 특정 경로를 아직 방문하지 않았다면 큐에 담아서 탐색을 진행한다.
DFS가 유리한 경우
- 재귀적인 특징과 백트래킹을 이용하여 모든 경우를 하나씩 전부 탐색하는 경우
- Graph의 크기가 클 경우
- Optimal한 답을 찾는 것이 아닌 경우
- 경로의 특징을 저장해야 하는 경우 ex) 경로의 가중치, 이동 과정에서의 제약
BFS가 유리한 경우
- 최단 거리 or 최단 횟수 구하는 경우
- Optimal한 답을 찾는 경우, BFS는 가장 처음 발견되는 해답이 최단 거리이다!
- 탐색의 횟수를 구해야 하는 경우 (7576번 토마토 문제)
2. 다이나믹 프로그래밍
동적 계획법(Dynamic Programming, DP)은 큰 문제를 작은 문제로 나누어서 푸는 방식의 알고리즘이다.
다이나믹 프로그래밍은 다음 조건을 만족할 때 사용할 수 있다.
- 최적 부분 구조(Optimal Substructure): 큰 문제를 작은 문제로 나눌 수 있다.
- 중복되는 부분 문제(Overlapping Subproblem): 동일한 작은 문제를 반복적으로 해결한다.
동적 계획법의 구현 방식에는 두 가지 방법이 있다.
- Top-down : 큰 문제를 작은 문제로 쪼개면서 푼다. 재귀로 구현
- Bottom-up : 작은 문제부터 차례대로 푼다. 반복문으로 구현
✅ 문제
https://www.acmicpc.net/problem/11727
✅ 풀이
import sys
input = sys.stdin.readline
N = int(input())
dp = [0] * 1001
dp[1] = 1
if N >= 2:
dp[2] = 3
for i in range(3, N+1):
dp[i] = (dp[i-2]*2) + dp[i-1]
print(dp[N]%10007)Bottom-up 방식으로 구현한 것이다.
Bottom-up
1. 문제를 크기가 작은 문제부터 차례대로 푼다.
2. 문제의 크기를 조금씩 크게 만들면서 문제를 점점 푼다.
3. 작은 문제를 풀면서 왔기 때문에, 큰 문제는 항상 풀 수 있다.
4. 반복하다 보면 가장 큰 문제를 풀 수 있다.
3. 그리디
그리디 알고리즘이란 현재 상황에서 가장 좋은 것(최선의 선택)을 고르는 알고리즘을 말한다. 그리디 알고리즘은 동적 프로그래밍을 간단한 문제 해결에 사용하면 지나치게 많은 일을 한다는 것을 착안하여 고안되었다. 이렇게 각 단계에서 최선의 선택을 한 것이 전체적으로도 최선이길 바라는 알고리즘인 것이다.
그리디 알고리즘을 이용하면 매 순간 가장 좋아 보이는 것만 선택하며, 현재의 선택이 나중에 미칠 영향에 대해서는 고려하지 않는다. 따라서 당장 좋아 보이는 것만 선택하므로, 최종적인 결과 도출에 대한 최적해를 보장해주는 것은 아니다.
하지만 코딩 테스트에서의 대부분의 그리디 문제는 탐욕법으로 얻은 해가 최적의 해가 되는 상황에서, 이를 추론할 수 있어야 풀리도록 출제가 된다.
그리디 알고리즘이 사용되는 예시
- AI에 있어서 결정 트리 학습법(Decision Tree Learning)
- 활동 선택 문제(Activity selection problem)
- 거스름돈 문제
- 최소 신장 트리(Minimum spanning tree)
- 제약조건이 많은 대부분의 문제
- 다익스트라 알고리즘
- 허프만 코드
- UNION & FIND 알고리즘
일반적인 그리디 알고리즘은 문제를 풀기 위한 최소한의 아이디어를 떠올릴 수 있는 능력을 요구하기 때문에 약간의 창의성이 필요하다.
✅ 문제
https://www.acmicpc.net/problem/2839
✅ 풀이
- 5kg 봉지만 이용하는 방법
- 5kg, 3kg 봉지 둘 다 이용하는 방법
- 3kg 봉지만 이용하는 방법
- 둘 다 안되는 경우 -> -1 출력
의 순위로 방법을 선택하면 될 것이므로 다음과 같이 코드를 짜볼 수 있겠다.
N = int(input())
count = 0
while N >= 0:
if N % 5 == 0:
count += N//5
print(count)
break
else:
N -= 3
count += 1
if N < 0:
print(-1)4. 분할 정복
분할 정복(Divide and Conquer)란 큰 문제를 작은 문제로 분할하고, 각각의 작은 부분 문제를 해결하여 전체 문제의 해답을 구하는 알고리즘이다. (동적 프로그래밍과의 차이점은 요기 아래에~) 문제의 크기가 커서 직접적인 해결이 어려운 경우 유용하다. 대표적인 예로, 정렬 알고리즘인 병햡 정렬(Merge Sort)과 퀵 정렬(Quick Sort)이 있다.
동작 방식은 다음과 같다.
- 분할: 문제를 작은 부분 문제들로 분할한다.
- 정복: 분할된 부분 문제들을 각각 재귀적으로 해결한다.
- 병합: 부분 문제들의 해답을 결합하여 전체 문제의 해답을 얻는다.
분할 정복 알고리즘의 시간 복잡도
일반적으로 부분 문제의 개수, 분할된 문제의 크기, 분할과정의 복잡도에 따라 결정된다.
대부분의 경우, 분할 정복 알고리즘은 재귀적인 방법으로 문제를 해결하므로, 재귀 호출의 깊이에 따라 시간 복잡도가 결정된다.
분할된 문제들의 크기가 일정하다면, 재귀 호출의 깊이는 로그 시간 복잡도에 비례한다.
분할된 문제의 개수가 N이라면, 시간 복잡도는 O(N*logN)
참고: [알고리즘/Python] 분할 정복(Divide and Conquer)
4.1 병합 정렬
분할과 정복을 모두 사용하여 리스트를 반으로 나누어 각각을 재귀적으로 정렬하고, 정렬된 두 개의 부분 리스트를 합쳐 전체 리스트를 정렬하는 방식
동작 과정
- 분할: 입력 리스트를 반으로 나눈다.
- 정복: 각각의 부분 리스트를 재귀적으로 병합 정렬한다.
- 결합: 정렬된 부분 리스트를 합쳐 전체 리스트를 정렬한다.

파이썬 구현 코드
def merge_sort(arr):
if len(arr) <= 1:
return arr
# Divide
mid = len(arr) // 2
left = arr[:mid]
right = arr[mid:]
# Conquer
left_sorted = merge_sort(left)
right_sorted = merge_sort(right)
# Combine
return merge(left_sorted, right_sorted)
def merge(left, right):
result = []
i, j = 0, 0
while i < len(left) and j < len(right):
if left[i] <= right[j]:
result.append(left[i])
i += 1
else:
result.append(right[j])
j += 1
result += left[i:]
result += right[j:]
return resultmerge_sort함수: 입력 리스트를 반으로 나누고 재귀적으로 호출하여 각각을 정렬, 마지막으로 merge 함수를 사용하여 두 정렬된 리스트를 합병하여 전체 리스트를 정렬merge함수: 두 개의 정렬된 리스트를 인수로 받아, 두 리스트를 비교하여 작은 순서대로 result 리스트에 삽입하고, 남은 요소를 추가하여 반환
✅ 문제
https://www.acmicpc.net/problem/2517
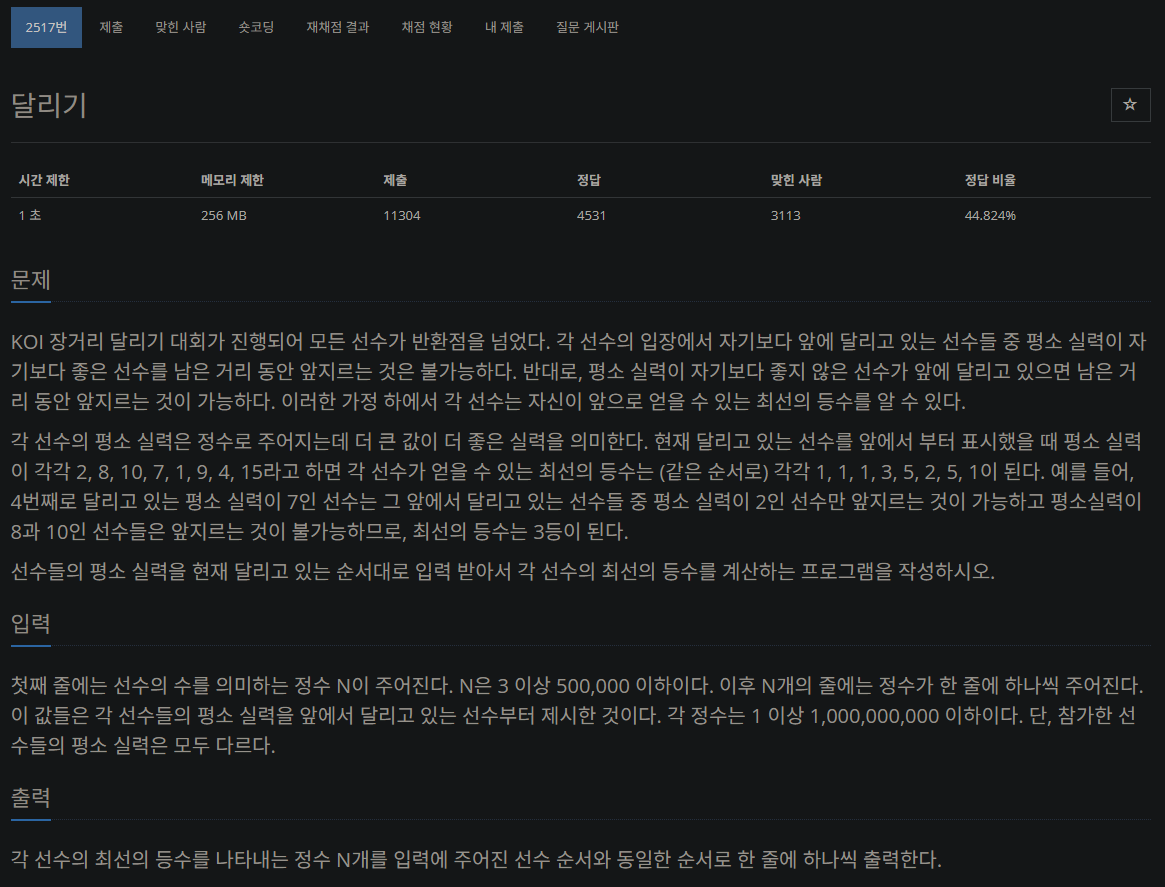
✅ 풀이
4.2 퀵 정렬
분할과 정복을 사용하여 리스트를 분할하고, 각각을 재귀적으로 정렬한 다음, 전체 리스트를 합치지 않고 원래 위치에 놓여있는 것을 기준으로 정렬
특히, 정렬을 위해 별도의 저장 공간을 필요로 하지 않아 메모리 사용량이 적다는 특징이 있다.
동작 과정
- 기준점(pivot) 선택: 리스트에서 하나의 원소를 기준점으로 선택한다.
- 분할: 기준점을 기준으로 리스트를 두 개로 분할한다. 분할된 두 개의 리스트는 각각 기준점보다 작은 값과 큰 값으로 이루어져 있다.
- 정복: 각각의 부분 리스트를 재귀적으로 퀵 정렬한다.
- 결합: 정렬된 부분 리스트를 합쳐 전체 리스트를 정렬한다.

파이썬 구현 코드
def quick_sort(arr):
if len(arr) <= 1:
return arr
# Divide
pivot = arr[0]
left = []
right = []
for i in range(1, len(arr)):
if arr[i] < pivot:
left.append(arr[i])
else:
right.append(arr[i])
# Conquer
left_sorted = quick_sort(left)
right_sorted = quick_sort(right)
# Combine
return left_sorted + [pivot] + right_sortedquick_sort 함수: 입력 리스트의 첫 번째 요소를 기준으로 왼쪽과 오른쪽 부분 리스트를 나눔, 재귀적으로 각각을 정렬하여 마지막으로 합쳐서 반환
- Binary Search(이진 탐색) 또한 분할 정복의 예시 중 하나이다.
✅ 문제
✅ 풀이
5. 이진 탐색 트리
이진 트리란, 트리의 종류로 각 노드가 최대 2개의 자식 노드를 갖는 트리를 말한다. 즉, 이진 트리의 각 노드는 자식 노드를 갖고 있지 않을 수도 있으며, 1개를 가질 수도, 2개를 가질 수도 있다.
이진 탐색 트리(Binary Search Tree, BST)는 이진 트리에서 어떠한 규칙에 따라 나열한 트리이다. 이 규칙은 모든 노드에 대해서 왼쪽 노드보다 오른쪽 노드가 더 크게 나열하는 것이다.

이진 탐색 트리는 평균 의 시간복잡도를 가지며 트리가 한쪽으로만 치우친 최악의 경우 의 시간복잡도를 가진다.
파이썬 코드 구현
class Node:
def __init__(self, key, value, left, right):
self.key = key
self.value = value
self.left = left
self.right = right
class BinarySearchTree():
def __init__(self) -> None:
self.root = None
# 검색하는 메서드
def search(self, key) -> int:
node = self.root # 루트
while True:
if node is None: # 더 이상 진행할 수 없으면
return -1 # 검색 실패
if key == node.key: # key와 노드 p의 키가 같으면
return node.value # 검색 성공
elif key < node.key: # key가 작으면
node = node.left # 왼쪽 서브 트리에서 검색
else: # key가 작으면
node = node.right # 오른쪽 서브 트리에서 검색✅ 문제
https://www.acmicpc.net/problem/1269
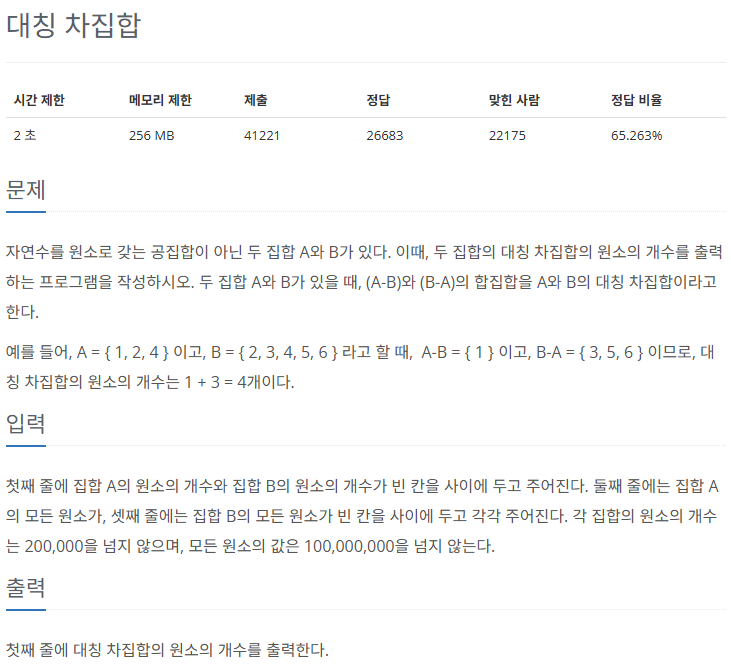
✅ 풀이
8. 각 알고리즘별 비교
8.1 DP vs 분할정복
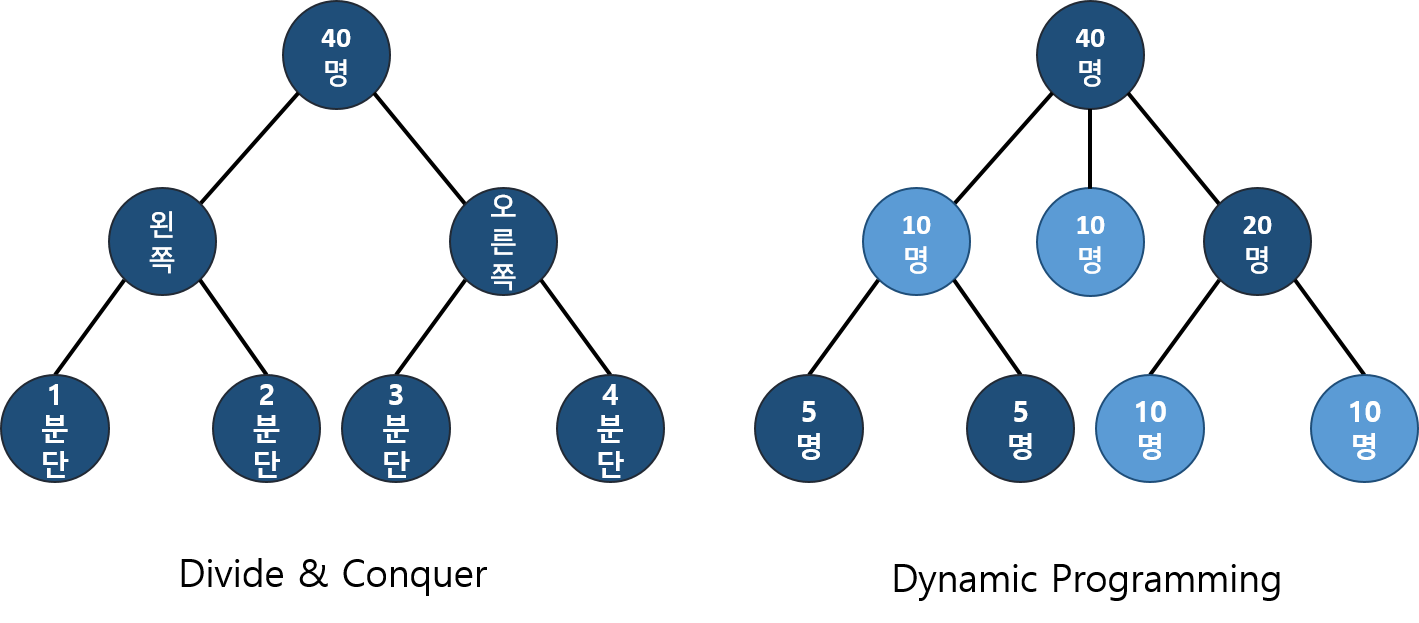
DP에서는 쪼개진 작은 문제가 중복되지만, 분할 정복은 작은 문제가 절대로 중복될 수 없다.
즉, 문제를 나누는 방식에서 차이가 있다. DP에서는 어떤 부분 문제는 두 개 이상의 문제를 푸는 데 사용될 수 있기 때문에, 이 문제의 답을 여러 번 계산하는 대신 한 번만 계산하고 그 결과를 재활용함으로써 속도 향상을 시킬 수 있다. 이때 이미 계산한 값을 저장해 두는 메모리를 캐시(cache)라고 부르며, 두 번 이상 계산되는 부분 문제를 중복되는 부분 문제(overlapping subproblems)라고 부른다.
어쨌든, 분할 정복은 작은 문제가 절대 중복되지 않으므로 메모이제이션 방식을 사용할 수 없다.
만약 주어진 문제를 작은 문제로 나누어 해결해야 할 때, 피보나치 수열과 같이 작은 문제 간 해가 중복될 수 있는 경우 분할 정복보다는 DP가 효율적인 이유이다.
8.2 이진 탐색 vs 이진 탐색 트리
근본적으로 같은 원리에 의한 탐색 구조를 갖는다.
- 이진 탐색: "배열"에 저장된 데이터를 탐색한다.
- 동적으로 크기가 변하는 데이터 집합 탐색에는 부적합
- 삽입과 삭제가 상당히 힘들다.
- 시간 복잡도:
- 이진 탐색 트리: "연결 리스트" 데이터에 대한 탐색이다.
- 비교적 빠른 시간 안에 삽입과 삭제를 끝마칠 수 있는 구조이다.
- 삽입, 삭제가 빈번히 이루어진다면 반드시 이진 탐색 트리를 사용해야 한다.
- 시간 복잡도:
균형트리:
불균형 트리: , 순차 탐색과 동일

