Binary tree - BFS

Binary Trees - BFS

DFS와 BFS의 차이

DFS (깊이 우선 탐색) 에서는 깊이(depth) 를 우선시하며, 가능한 한 트리의 아래로 내려가며 탐색을 진행합니다. 루트에서 시작해 가능한 한 아래로 내려간 후, 더이상 내려갈 수 없을 때 다음 경로를 탐색합니다.

BFS (너비 우선 탐색 - breadth-first search) 에서는 너비(breadth) 를 우선시하며, 같은 깊이의 모든 노드를 탐색한 후 다음 깊이로 이동합니다.

• DFS의 탐색 순서 (depth):
  - 깊이를 늘려가며 탐색 : 0, 1, 2, 3, 4, ...
  
• BFS의 탐색 순서 (depth):
  - 같은 깊이의 노드부터 탐색: 0, 1, 1, 2, 2, 2, 2, ...
  

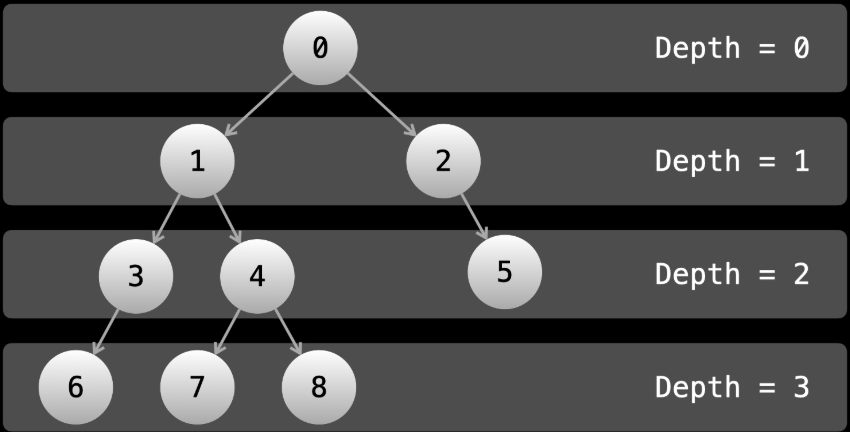
완전 이진 트리(Complete Binary Tree) 와 BFS

완전 이진트리란

• 마지막 레벨은 제외한, 모든 레벨이 가득 차 있으며
• 마지막 레벨에서는 가능한 한 왼쪽부터 노드가 채워진 트리입니다.

트리의 깊이(depth)를 레벨(Level)로 볼 수 있습니다.

BFS의 동작 원리

BFS는 주어진 깊이(d) 에 있는 모든 노드를 방문 후, 다음 깊이(d+1)로 넘어갑니다. BFS는 Queue를 사용하여 구현합니다.

• DFS와의 차이
  • DFS는 Stack 이나 재귀(recursion) 사용
  • BFS는 Queue 를 사용하여 구현
  • BFS를 재귀로 구현하는 것은 비효율적이고 복잡하며, 어떤 이득도 없습니다.

BFS와 DFS 선택 기준

1. 모든 노드를 방문해야 하는 문제
   • BFS와 DFS 중 어느 것을 사용해도 상관없습니다.
   • DFS는 코드가 더 간단하고 빠르게 구현 가능하므로 이 경우를 많이 사용됩니다.
2. 레벨 기반으로 처리해야 하는 문제
   • BFS가 더 적합합니다.
   • ex) 트리의 각 레벨에서 특정 값을 계산하는 문제

BFS의 단점

1. 시간 낭비

• 찾고자 하는 값이 트리의 아래쪽에 있으면, BFS는 위쪽 레벨을 모두 탐색한 후에야 해당 값을 찾습니다.

2. 공간 복잡도

• BFS는 가장 많은 노드를 포함한 레벨의 노드를 모두 메모리에 저장해야 합니다.
• 예를 들어, 완전 이진 트리에서는 마지막 레벨에 가장 많은 노드가 존재하므로 공간 복잡도가 클 수 있습니다.

DFS와 BFS의 공간 복잡도

DFS

• 공간복잡도는 트리의 깊이(높이)와 선형적으로 관련
• 완전 이진 트리에서는 𝑂(log𝑛), 한쪽으로 치우친 트리에서는 𝑂(𝑛)

BFS

• 공간 복잡도는 특정 레벨의 최대 노드 수와 선형적으로 관련
• 완전 이진 트리에서는 𝑂(𝑛) (마지막 레벨의 모든 노드가 메모리에 저장되기 때문).

BFS의 시간 복잡도

• 시간 복잡도는 트리의 총 노드 수에 비례: 𝑂(𝑛).
• 각 노드를 한 번 방문하고, 일정한 작업을 수행하는 것이 일반적

BFS 코드 구현 방식

1. Queue를 사용

• 큐는 현재 레벨의 모든 노드를 저장합니다.
• 큐에서 노드를 꺼내 방문하고, 해당 노드의 자식 노드를 큐에 추가합니다.
• 큐는 다음 레벨의 모든 노드를 포함하게 됩니다.

2. 반복문 기반으로 구현

• 각 레벨의 노드를 처리한 후, 다음 레벨로 넘어갑니다.

BFS의 활용

• BFS는 주로 레벨별 탐색이 필요할 경우에 좋습니다
• 예를들어
  - 그래프의 최단 경로 탐색
  - 트리의 레벨별 처리