Dynamic Programming (DP)
동적 프로그래밍이란?
동적 프로그래밍은 복잡한 문제를 작은 하위 문제로 나누어 해결한 뒤, 중복되는 계산을 줄이기 위해 결과를 저장(memoization)하여 최적화하는 알고리즘 설계 기법입니다.
memoization 이해
1️⃣ 문제 정의
피보나치 수열은 다음과 같은 점화식으로 정의됩니다:
𝐹(0)=0
F(1)=1
F(n)=F(n−1)+F(n−2) (n ≥ 2)
즉, 각 숫자는 이전 두 숫자의 합으로 계산됩니다.
2️⃣ 단순 재귀 (기본적인 접근법)
가장 단순한 방법으로 재귀를 사용합니다.
def fibonacci(n):
if n <= 1:
return n
return fibonacci(n-1) + fibonacci(n-2)
예제
fibonacci(5)를 호출하면 다음과 같이 동작합니다:
F(5)=F(4)+F(3)
F(4)=F(3)+F(2)
F(3)=F(2)+F(1)
F(2)=F(1)+F(0)
문제점: 반복 계산
F(3)와 F(2)는 여러 번 계산됩니다.
시간 복잡도: O(2^n) (지수적으로 증가)
3️⃣ 메모이제이션 적용
메모이제이션(Memoization)은 이전에 계산한 값을 저장하여, 동일한 값을 다시 계산하지 않도록 최적화하는 기법입니다.
메모이제이션 단계별 적용
- 값 저장소 준비: 계산 결과를 저장할 자료 구조를 준비합니다. 여기서는 딕셔너리(memo)를 사용합니다.
- 값 확인: 함수가 호출될 때, 이미 계산된 값이 저장소에 있다면 그 값을 반환합니다.
- 새로운 값 계산 및 저장: 저장소에 없는 값은 계산한 후 저장합니다.
def fibonacci(n, memo={}): # memo: 저장소
if n in memo: # 1. 이미 계산된 값이면 반환
return memo[n]
if n <= 1: # 2. 기본 값 반환
return n
# 3. 새로운 값 계산 및 저장
memo[n] = fibonacci(n-1, memo) + fibonacci(n-2, memo)
return memo[n]
fun fibonacci(n: Int, memo: MutableMap<Int, Int> = mutableMapOf()): Int {
if (n <= 1) return n
// 이미 계산된 값이 있다면 반환
if (memo.containsKey(n)) return memo[n]!!
// 새로운 값 계산 후 저장
memo[n] = fibonacci(n - 1, memo) + fibonacci(n - 2, memo)
return memo[n]!!
}
4️⃣ 동작 과정
예를 들어 fibonacci(5)를 호출하면:
- memo = {} 초기화
- fibonacci(5) 호출
F(5)=F(4)+F(3) - fibonacci(4) 호출
F(4)=F(3)+F(2) - fibonacci(3) 호출
F(3)=F(2)+F(1) - fibonacci(2) 호출
F(2)=F(1)+F(0)
F(2)=1+0=1
저장: memo = {2: 1} - fibonacci(3) 계산 완료
F(3)=1+1=2
저장: memo = {2: 1, 3: 2} - fibonacci(4) 계산 완료
F(4)=2+1=3
저장: memo = {2: 1, 3: 2, 4: 3} - fibonacci(5) 계산 완료
F(5)=3+2=5
저장: memo = {2: 1, 3: 2, 4: 3, 5: 5}
최종 결과: fibonacci(5) = 5
5️⃣ 시간 복잡도 분석
메모이제이션을 통해 중복 계산이 제거됩니다.
각 값은 한 번만 계산되므로 시간 복잡도는 O(n)입니다.
공간 복잡도는 저장소 크기 때문에 O(n)입니다.
6️⃣ 메모이제이션에서 테이블로 확장 (Bottom-Up 방식)
메모이제이션은 재귀 기반(탑다운)으로 작동합니다. 이제 이를 반복문 기반(바텀업) 방식으로 구현해보겠습니다.
메모이제이션 대신 반복문을 사용하여 작은 값부터 큰 값을 계산하는 방식입니다. 이를 Tabulation 이라고 합니다.
def fibonacci(n):
if n <= 1:
return n
dp = [0] * (n+1) # 테이블 초기화
dp[1] = 1 # 기본 값 설정
for i in range(2, n+1):
dp[i] = dp[i-1] + dp[i-2] # 점화식 적용
return dp[n] # 최종 값 반환
fun fibonacci(n: Int): Int {
if (n <= 1) return n
// DP 테이블 초기화
val dp = IntArray(n + 1)
dp[0] = 0
dp[1] = 1
// 점화식 적용
for (i in 2..n) {
dp[i] = dp[i - 1] + dp[i - 2]
}
return dp[n]
}
dp 테이블을 사용하여 0부터 𝑛까지 값을 채워나갑니다.
저장된 값을 활용하므로, 시간 복잡도는 𝑂(𝑛), 공간 복잡도도 𝑂(𝑛)입니다.
7️⃣ 메모리 최적화 (Bottom-Up + 공간 최적화)
테이블을 사용하지 않고, 이전 두 값만 저장하여 공간 복잡도를 줄일 수 있습니다.
def fibonacci(n):
if n <= 1:
return n
prev, curr = 0, 1 # 초기 값
for _ in range(2, n+1):
prev, curr = curr, prev + curr # 값 갱신
return curr
fun fibonacci(n: Int): Int {
if (n <= 1) return n
var prev = 0
var curr = 1
for (i in 2..n) {
val temp = curr
curr += prev
prev = temp
}
return curr
}
- curr=prev+curr로 값을 갱신.
- 𝑛번째 값을 반환.
이전 두 값만 유지하므로, 공간 복잡도는 𝑂(1)입니다. (배열이나 Map을 사용하지 않음)
시간 복잡도: 𝑂(𝑛)
5️⃣ 비교
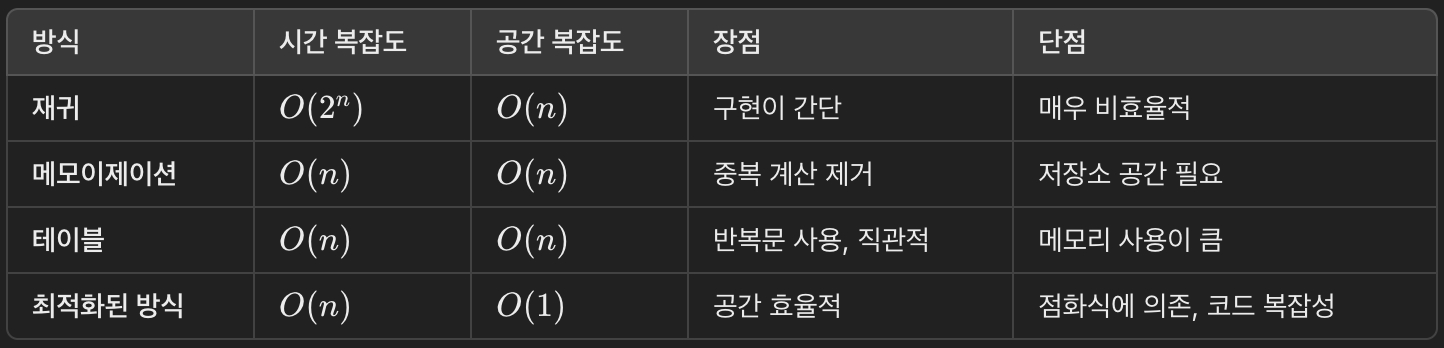
- 메모이제이션은 탑다운 방식으로 중복 계산을 줄이는 기법입니다.
- 반복문과 테이블을 활용한 바텀업 방식도 동일한 결과를 얻을 수 있습니다.
- 피보나치 수열은 동적 프로그래밍의 기본 예제로, 메모이제이션과 테이블 방식의 차이를 이해하기 좋습니다.

