[Algo] 최소 공통 조상(Lowest Common Ancestor, LCA)

그래프와 표 곳곳에 오타가 있을 수도 있음에 주의

---

이런 트리가 주어졌을 때, 4번, 10번 노드의 공통 조상들에는 2번, 1번 노드가 있다.

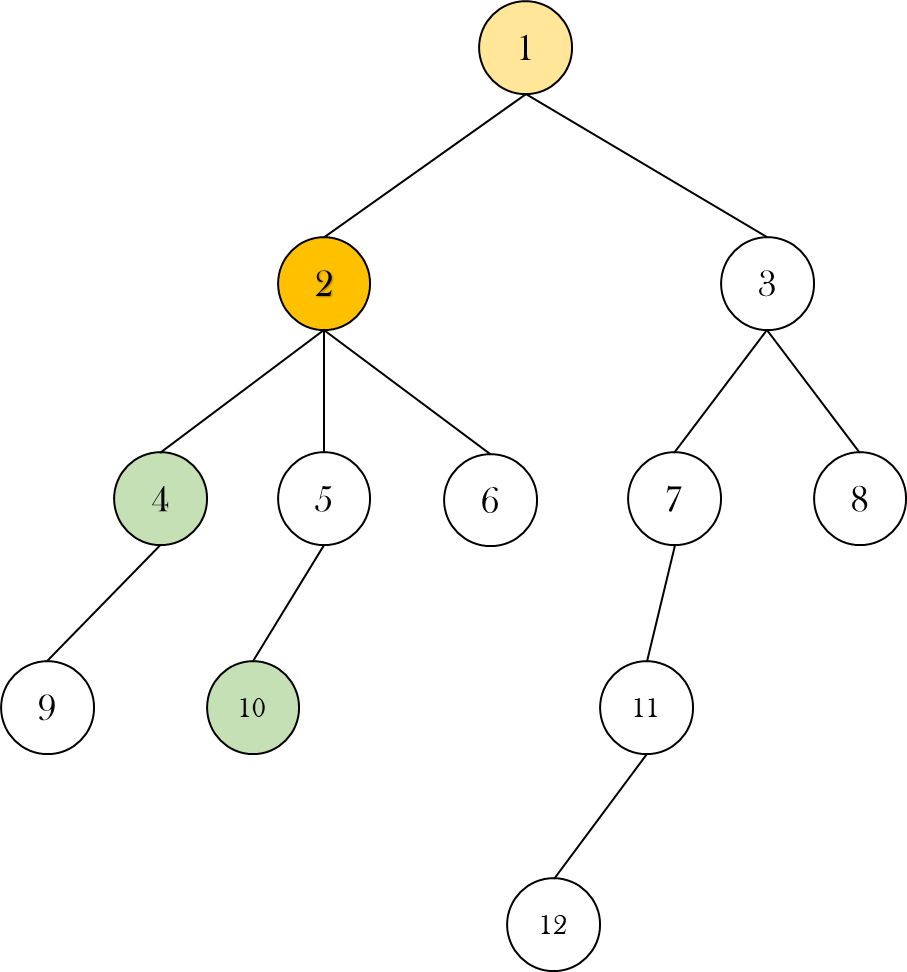
이 중 가장 아래에 있는 2번 노드를 가리켜 4번, 10번 노드의 최소 공통 조상(LCA)이라고 한다.

---

LCA 알고리즘 (1) (문제 : 가장 가까운 공통 조상)

(i) 간선 정보가 주어질 때, 각 노드의 깊이와 해당 노드의 부모 노드를 저장하며 트리를 만든다.

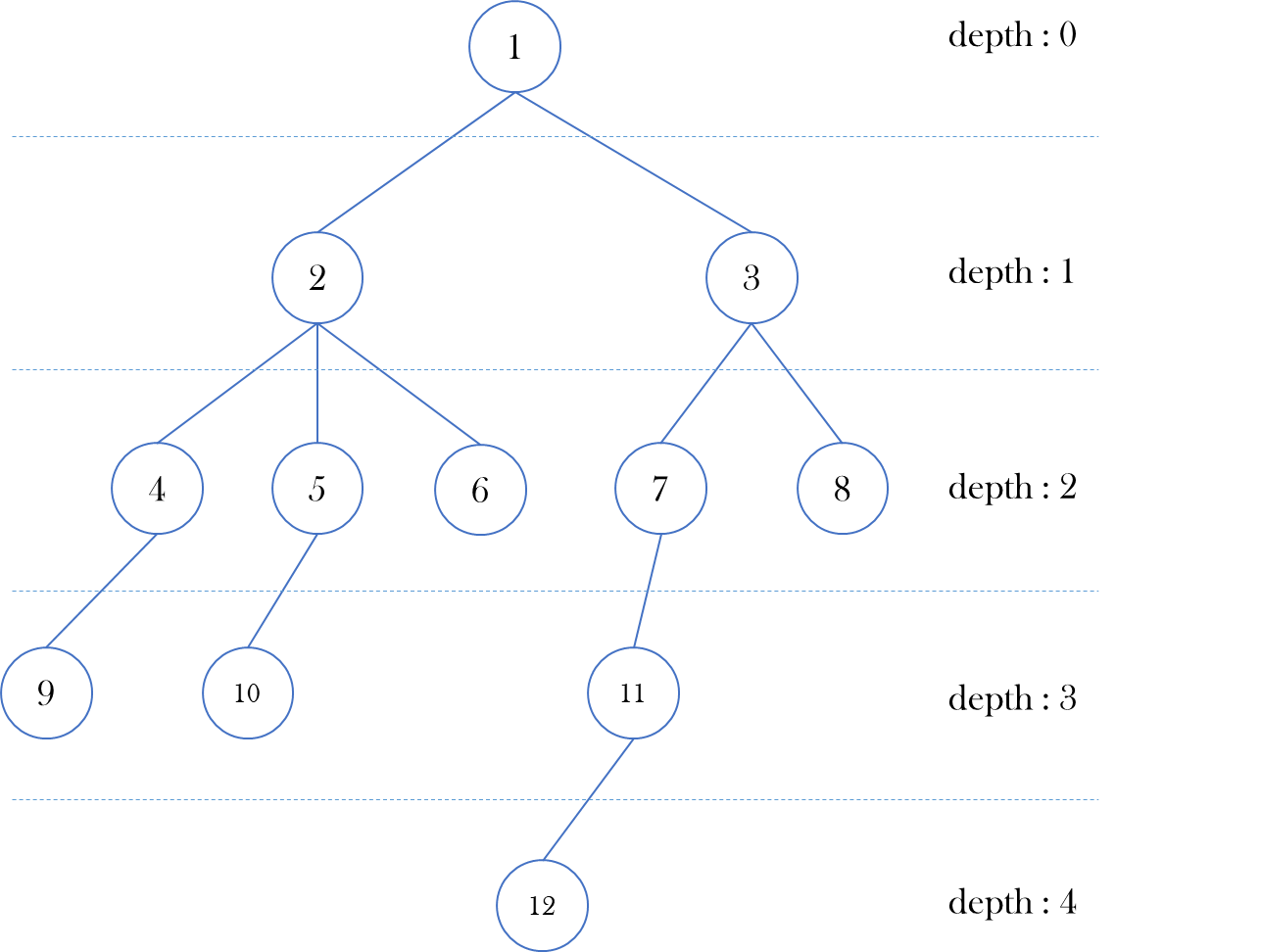
(ii) 최소 공통 조상을 구해야 하는 두 노드가 주어지면 우선 두 노드의 깊이를 확인한다.

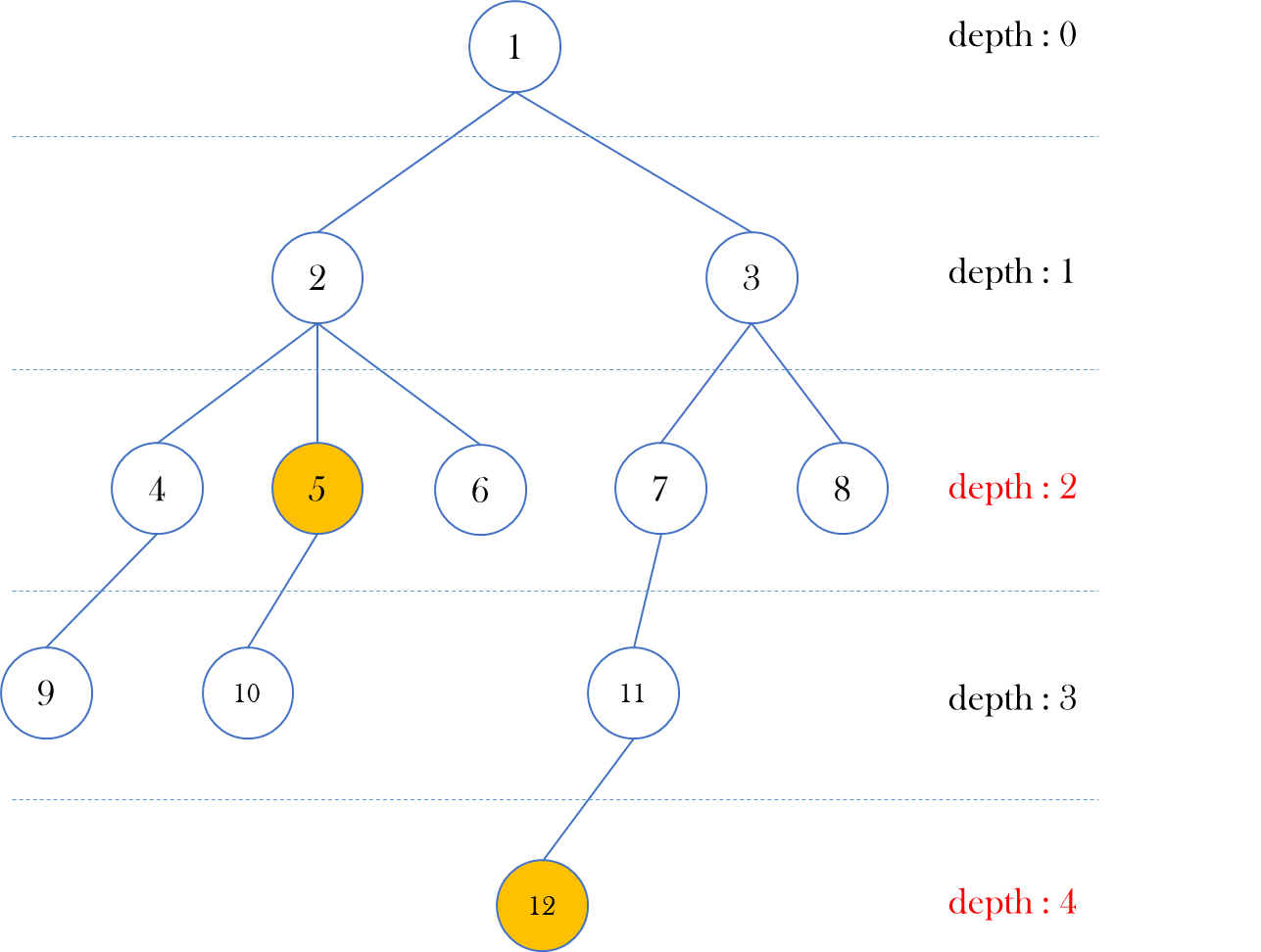
(iii) 만약 두 노드의 깊이가 서로 다르다면 좀 더 깊이 있는 노드를 루트 방향으로 거슬러 올라가면서 두 노드의 깊이를 맞추어 준다.

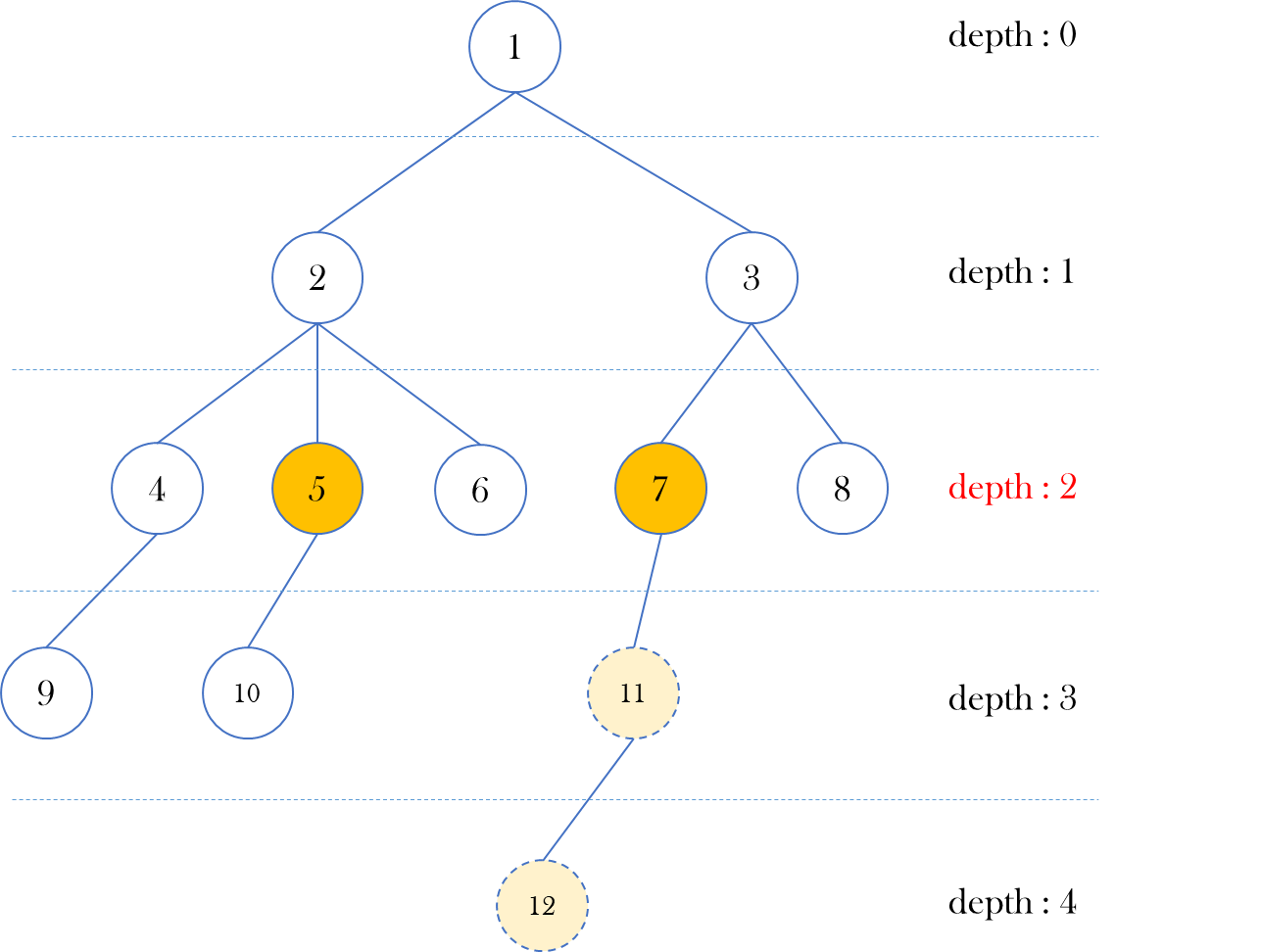
(iv) 만약 여전히 두 노드가 서로 다르다면 두 노드가 서로 같은 노드가 될 때까지 둘을 모두 위로 올려본다.

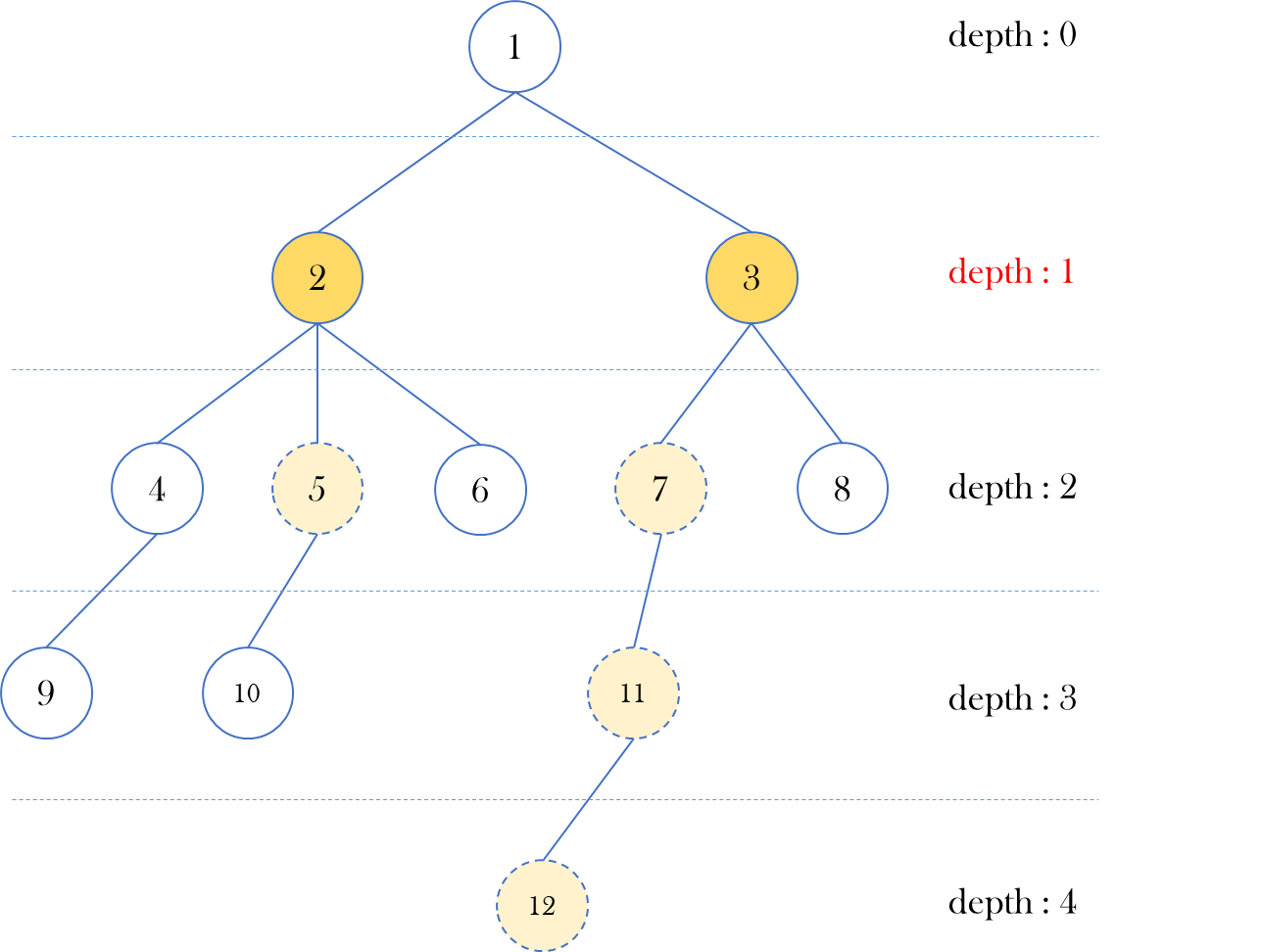
(v) 언젠가 두 노드가 서로 같은 노드가 된다면 그 노드가 입력된 두 노드의 최소 공통 조상이 된다.

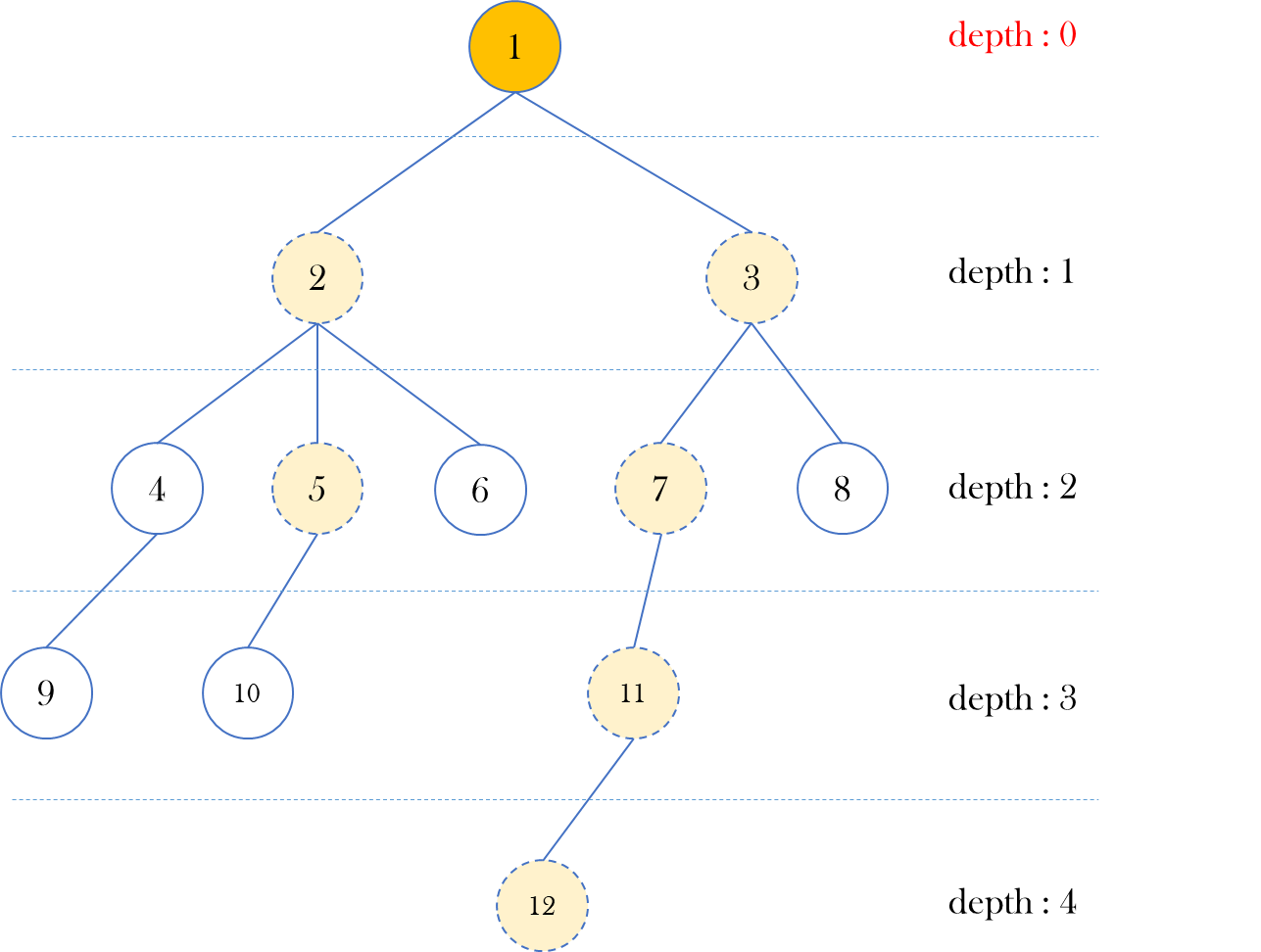
위 트리의 최대 깊이를 $d$라고 할 때, 위 알고리즘의 시간 복잡도는 $O(d)$가 된다.

int findLSA(int u, int v){
	if (depth[u] < depth[v]) swap(u, v); // 좀 더 깊이 있는 노드를 선택한다.

	while (depth[u] != depth[v]) {       // 두 노드의 깊이가 서로 같아질 때까지 더 깊이 있는 노드의 조상을 찾아보자
		u = parent[u]; 
	}
	while (u != v){                      // 깊이가 서로 같음에도 두 노드가 서로 다르다면
		u = parent[u];                     // 이번에는 두 노드를 함께 위로 올려준다.
		v = parent[v];                     // 두 노드는 언제나 루트 노드의 자손들이므로 이 과정이 끝나지 않는 경우는 발생하지 않는다.
	}
	return u;                            // 최소 공통 조상을 리턴
}

---

LCA 알고리즘 (2) Sparse Table (문제 : LCA 2)

위의 LCA 알고리즘(1)의 시간 복잡도가 $O(d)$($d$는 트리의 최대 깊이)라면, 노드가 아주 많이 주어지는 경우에는 어떻게 될까?

만약 트리의 균형이 깨져 다음과 같은 트리가 만들어졌다고 해보자

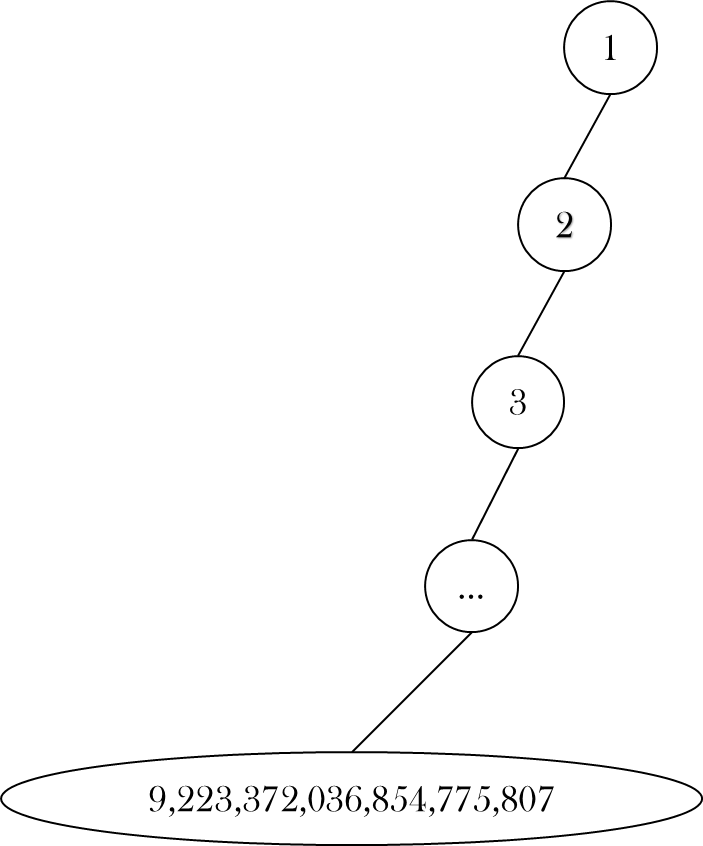
여기에서 1번 노드와 9,223,372,036,854,775,807$(=2^{63}-1)$번 노드의 공통 조상을 찾기 위해서 위 LCA 알고리즘(1)을 사용한다면 반드시 시간 초과에 빠지게 될 것이다. 다행히 노드가 꽤 많이 주어지는 경우에도 특정 두 노드의 최소 공통 조상을 $\log d$의 시간에 찾아낼 수 있는 방법이 있다.

(i) 알고리즘의 전체적인 맥락은 첫 번째 알고리즘과 동일하지만, 1차원 배열에 자신의 부모 노드만을 저장했던 첫 번째와는 달리 이번에는 2차원 배열에 자신의 $2^i$번째 조상을 저장한다.(이를 가리켜 Sparse Table이라 함)

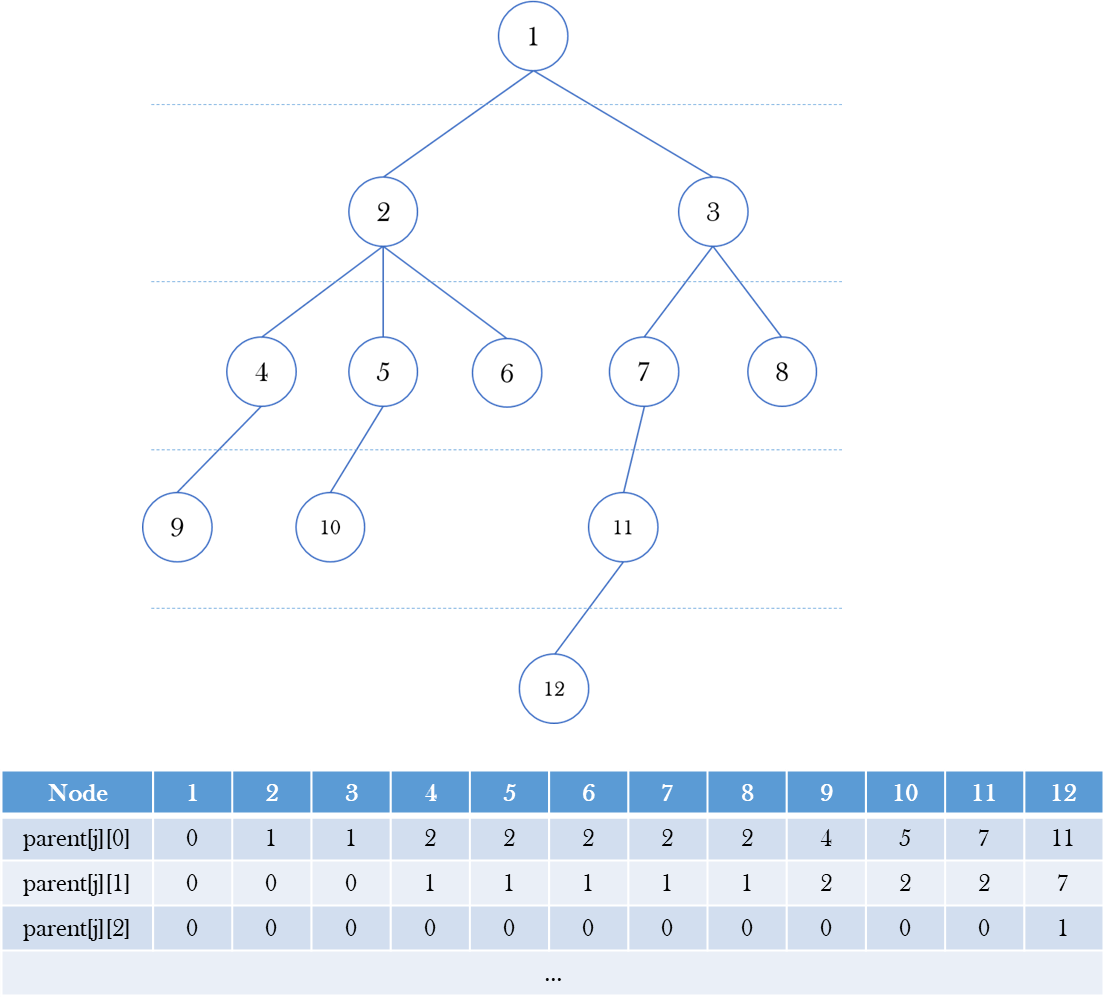
즉 parent[j]에는 j번 노드의 1, 2, 4, 8, 16, … 번째 조상이 무엇인지가 저장되어 있다.

(ii) 이번에도 5번, 12번 노드의 LCA를 찾아보자

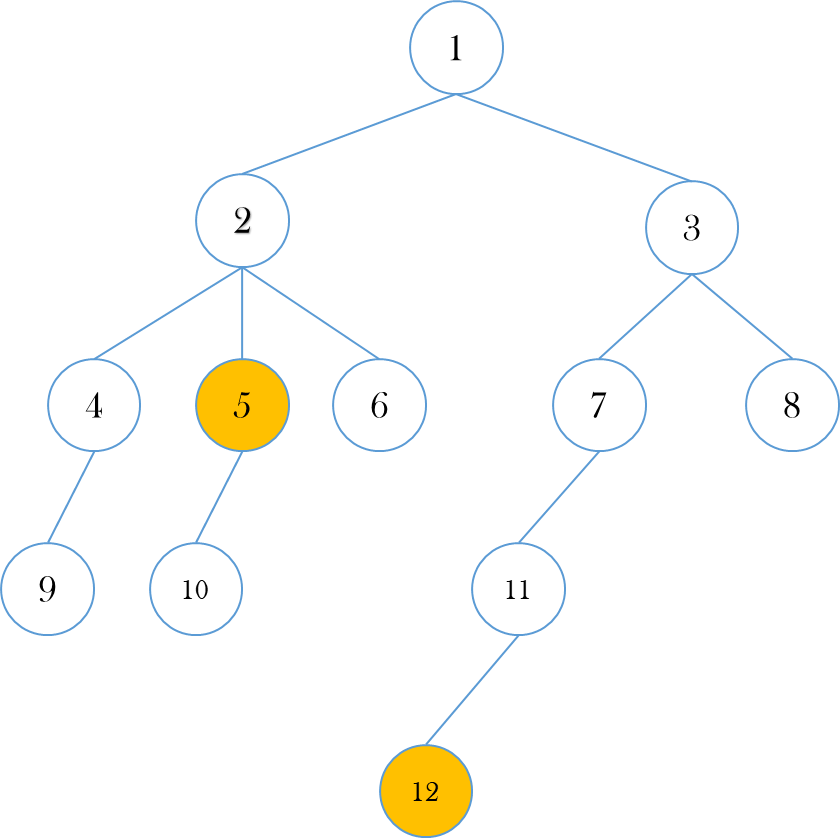
12번 노드가 더 깊이 있으므로 이번에도 5번 노드와 같은 높이로 올려줘야 한다.

만약 12번 노드의 3번째 부모를 찾으려면 어떻게 해야할까? 3을 이진수로 나타내면 $11_{(2)}$이므로 12번 노드의 3번째 부모를 찾으려면 12번 노드의 $2^0$번째 조상의 $2^1$번째 조상을 찾으면 된다. 즉 12번 노드의 $n$ 번째 조상을 찾으려면 $n$의 0번째, 1번째, …. 비트를 돌면서 1인 비트 자리($k$)를 찾아서 $2^k$번째 조상을 찾아나가면 된다.

배열 parent[12] 에는 12번 노드의 $2^0, 2^1,...$번째 조상들이 저장되어있으니 이를 보면서 $n$번째 조상을 찾을 수 있다.

5번 노드와 12번 노드의 깊이의 차이는 2이고 이를 2진수로 나타내면 $10_{(2)}$이다. 바로 $2^1$번째 조상을 찾아가자

if (depth[a] < depth[b]) swap(a, b);
	int diff = depth[a] - depth[b];				// 두 노드의 깊이 차이

	for (int i = 0; i < MAX_DEPTH; i++){
		if (diff & (1 << i)) a = parent[a][i];		// 깊이 차이만큼 올려주기
	}
}

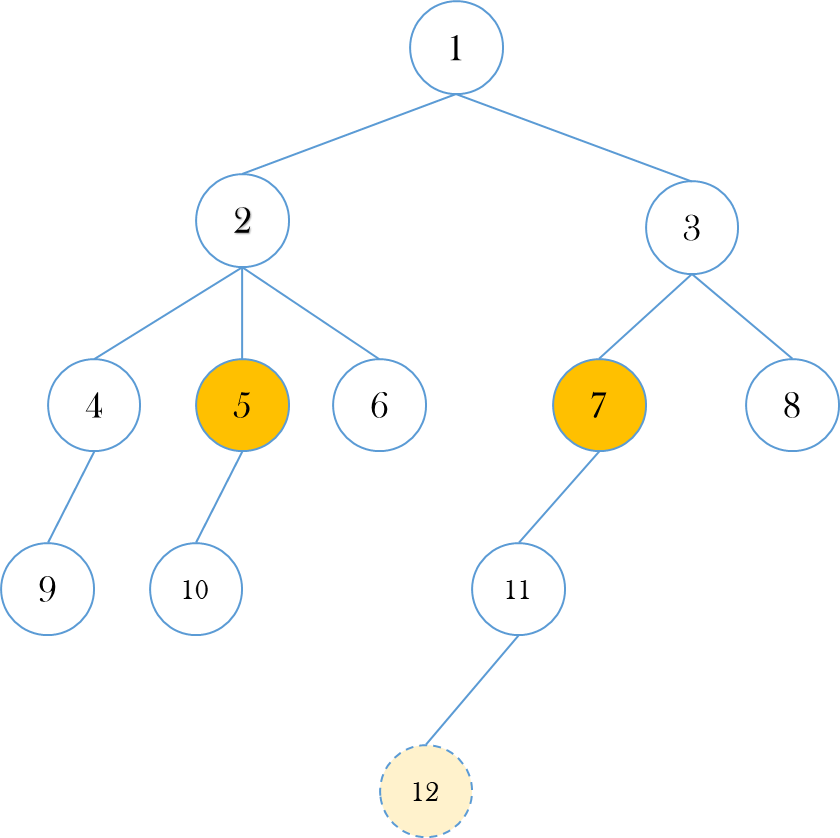
(iii) 두 노드의 높이를 맞췄는데 두 노드가 서로 다른 노드라면 이번에는 둘을 함께 올려주면 된다. 어떻게 올릴 수 있을까?

아래와 같은 트리가 있고 8번, 9번 노드의 LCA를 구하고 싶다고 하자.

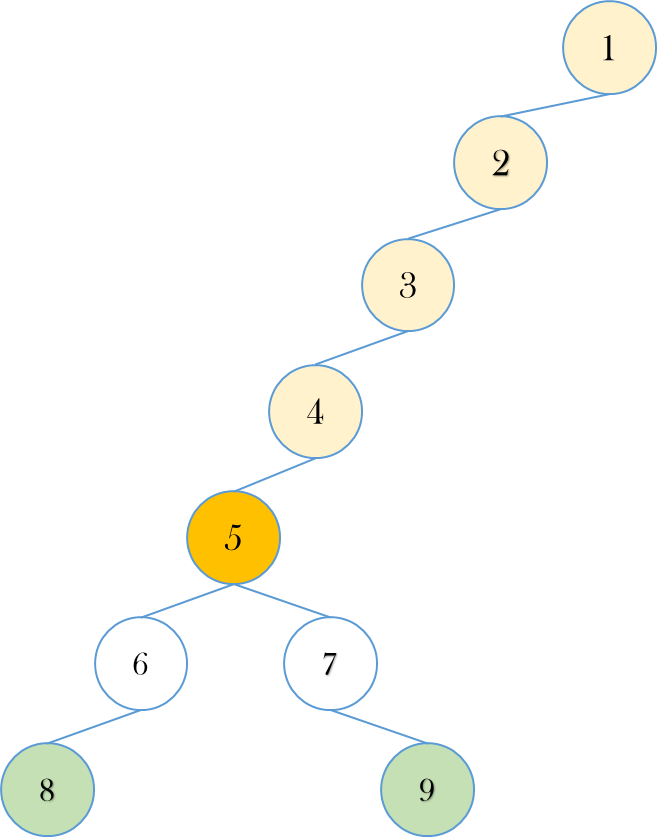
이 트리에서 확인할 수 있는 것은 8, 9번의 LCA인 5번 노드의 조상 노드들은 모두 8, 9번 노드의 공통 조상 노드이기도 하다는 것이다.

따라서 8, 9번 노드와 LCA까지의 깊이 차이를 $d$라고 할 때, 다음과 같은 두 경우가 있을 수 있다.

1) 만약 8번 노드의 $2^i$번째 노드와 9번 노드의 $2^i$번째 노드가 동일하다면, $d \leq 2^i$이다.

2) 한편 8번 노드의 $2^i$번째 노드와 9번 노드의 $2^i$번째 노드가 동일하지 않다면, $d > 2^i$가 될 것이다.

만약 두 번째 경우라면, 8, 9번 노드는 각각 $2^i$만큼 위로 올려 줘도 괜찮다. 이를 반복하면 두 노드는 두 노드의 최소 공통 조상의 정확히 아래에 위치하게 된다. (즉 $d-1$번째 조상!)

if (a != b) {
	for (int j = MAX_DEPTH - 1; j >= 0; j--) {			// 조상들을 보면서
		if (parent[a][j] && parent[a][j] != parent[b][j]) {	// 2^j 조상이 있고, 그것들이 서로 다른 경우
			a = parent[a][j];				// 두 노드는 2^j만큼 위로 올려줘도 좋다.
          		b = parent[b][j];                                   
		}
	}
	a = parent[a][0];						// 이 두 노드가 LCA의 정확히 아래에 위치하므로 그 부모를 찾으면 그 노드가 바로 LCA이다.
}

LCA 알고리즘 (3) Euler Tour Technique

오일러 투어를 이용해서 LCA를 찾아보자

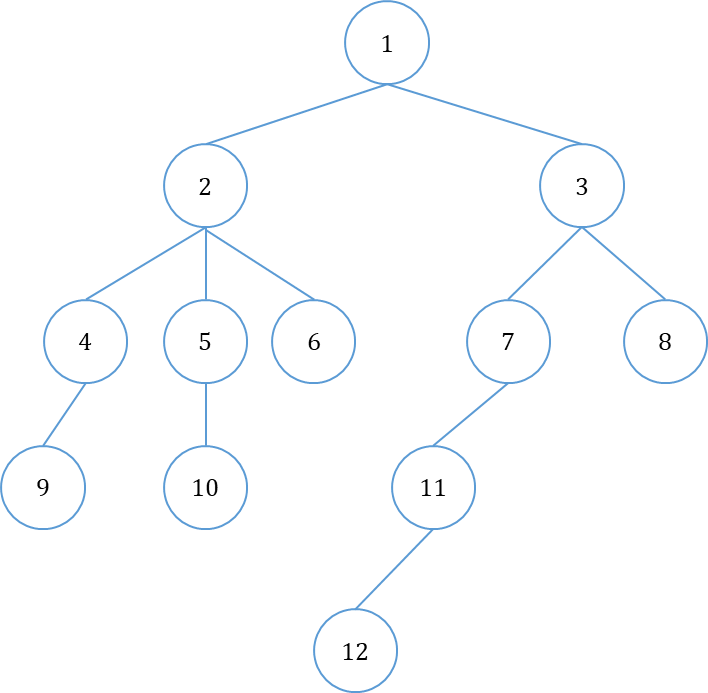
위 트리의 정점들을 오일러 투어로 방문한 순서대로 저장하면 다음과 같은 길이 $2 N-1$의 배열을 얻을 수 있다.

5번 노드와 12번 노드의 LCA를 찾으려고 한다면 배열 node 에서 5와 12가 가장 먼저 등장하는 구간에서 depth가 가장 작은 노드(여기서 답은 1)를 찾으면 된다.

주어진 특정 구간에서 최솟값을 찾을 때에는 세그먼트 트리를 쓰면 되고 그 시간 복잡도는 $O(\log N)$이다.