
평면 상에 주어진 개의 선분들 중 교차하는 것이 있는지는 샤모스-호이 알고리즘(Shamos-Hoey Algorithm)을 통해 의 시간에 판정할 수 있었다. 그러면 여기서 더 나아가 선분 교차점의 개수는 몇 개인지, 또 그 교차점들은 어디에 있는지도 궁금하지 않을까? (아님 말고)
오늘 다룰 벤틀리-오트만(Bentley-Ottmann) 알고리즘은 샤모스-호이 알고리즘을 확장한 것으로, 선분 교차점의 위치를 의 시간에 알아내는 알고리즘이다(는 교점의 개수).
1. 샤모스-호이 알고리즘 리뷰
벤틀리-오트만 알고리즘으로 넘어가기 전에, 샤모스-호이 알고리즘에서 정의했던 관계를 다시 보고 가자.
(1) 비교 가능함과 위에 있음.
평면 상의 두 선분 에 대해, 두 선분 모두와 교차하는 수직선 가 존재하면, 두 선분은 에서 비교가능(comparable)하다.
비교가능한 두 선분 와 그때의 수직선 에 대해, 와 의 교점의 좌표가 와 의 교점의 좌표보다 크거나 같다면 는 에서 보다 위에 있다고 하며, 다음과 같이 표기한다.
주어진 선분들의 두 끝점들을 정렬하고 왼쪽부터 스위핑한다. 스위핑 중 어떤 선분의 왼쪽 끝점을 만나면 해당 선분을 자료구조 에 집어넣고, 오른쪽 끝점을 만나면 에서 해당 선분을 제거한다. 선분을 자료구조에 넣거나 빼면서 새롭게 생기는 순서상 연속인 선분쌍들에 대해 교차 판정을 실시하고 만약 교차하는 것이 있다면 즉시 반환한다.
2. 벤틀리-오트만 알고리즘
이번에도 다음을 가정하고,
- 축에 수직인 선분은 없다.
- 세 선분이 한 점에서 만나는 경우는 없다.
여기에 추가로 다음도 가정하자.
- 서로 겹치는 선분도 없다(둘 이상의 점에서 서로 만나는 선분은 없다)
- 모든 이벤트 지점(즉 선분 끝점 및 선분 교차점)의 좌표는 서로 다르다.
전체적인 플로우는 샤모스-호이 알고리즘과 비슷하다. 새롭게 순서상 연속이 되는 경우가 나타날 때마다 선분 교차 판정을 실시해보는 것이다. 샤모스-호이 알고리즘에서는 서로 교차하는 선분이 나타나면 즉시 종료하면 됐기 때문에 선분의 삽입 및 제거가 일어날 때만 선분 교차 판정을 실시했다.
벤틀리-오트만 알고리즘도 마찬가지다. 차이가 있다면 이제는 서로 교차하는 두 선분들을 찾았을 때 알고리즘이 종료되지 않고, 그 교점이 새로운 이벤트로 추가된다는 것이다.
우리는 다음의 두 사실을 알고 있다.
- 교차하는 두 선분의 경우, 교차점을 기준으로 그 순서가 서로 바뀌고,
- 두 선분이 서로 교차한다면 반드시 두 선분이 순서상 서로 연속적(consecutive)으로 나타나는 수직선 가 존재한다(세 선분이 한 점에서 만나는 경우는 없다고 가정하는 경우).
어떤 두 선분 가 한 점 (단 가 나 의 끝점은 아니라고 가정.)에서 교차한다고 하자. 세 선분이 한 점에서 만나는 경우가 없다면, 이 두 선분은 점 의 직전과 직후에서 서로 순서상 연속이고, 를 지나면서 그 순서는 서로 바뀐다.
선분의 삽입과 삭제에서 그랬듯 두 선분의 순서를 서로 바꾸는 연산은 에 담긴 선분들의 순서를 바꾸고, 이렇게 순서가 바뀌면 새롭게 순서상 연속하게 되는 선분쌍들이 생겨날 수도 있다.
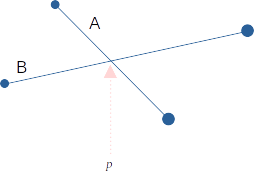
따라서 두 선분의 교차점 에서 새로운 이벤트를 추가해 처리해야한다.
이렇게 이벤트를 추가(그리고 제거)하기 위한 자료구조가 필요해지는데, 이를 라 하자. 는 다음의 연산을 수행할 수 있어야 한다.
i. INSERT(p, Q): 점 p를 Q에 삽입한다.
ii. DELETE(p, Q): 점 p를 Q에서 삭제한다.에는 각 선분의 양 끝점들과 스위핑을 하면서 얻게 되는 선분 교차점들을 담는데, 우리는 스위핑을 왼쪽에서 오른쪽으로 수행하므로 또한 이벤트가 일어나는 점들을 항상 축에 대해 오름차순으로 정렬한 채로 가지고 있을 수 있어야 한다.
이벤트를 담기 위한 자료구조 와 더불어, 선분을 담기 위한 자료구조 에도 변경점이 있다. 샤모스-호이 알고리즘에서 정의했던 연산들(아래 i ~ iv)에 추가로, 는 에 담긴 두 선분 의 위아래 순서를 서로 바꾸는 연산도 수행할 수 있어야 한다.
i. INSERT(s, T): 선분 s를 T에 삽입한다.
ii. DELETE(s, T): T에서 선분 s를 삭제한다.
iii. ABOVE(s, T): T에 담긴 선분들 중 s 바로 위에 있는 선분을 반환한다.
iv. BELOW(s, T): T의 선분들 중 s 바로 아래에 있는 선분을 반환한다.
v. SWAP(A, B, T): T에서 A, B의 순서를 서로 바꾼다.(1) Pseudo-code
BENTLEY-OTTMANN ALGORITHM (Bentley & Ottmann, 1979를 수정)
Q := the set of all endpoints of segments, stored in order by x-values
FOREACH point p in Q (in ascending x-order) Do
// Let S be the segment passing through p.
IF p is the left endpoint of S THEN BEGIN
INSERT(S, T);
A := ABOVE(S, T);
B := BELOW(S, T);
IF A intersects S THEN
// Let q be the intersection of segments S and A;
INSERT(q, Q);
IF B intersects S THEN
// Let q be the intersection of segment S and B;
INSERT(q, Q);
END;
ELSE IF p is the right endpoint of S THEN BEGIN
A := ABOVE(S, T);
B := BELOW(S, T);
IF A intersects B THEN
// Let q be the intersection of segment A and B;
INSERT (q, Q);
DELETE(S, T);
END;
ELSE BEGIN // p is the intersection of some two segments
// Let U, L be the segments passing through p, and U is the upper one
SWAP(U, L, T);
// L is now above U
A := ABOVE(L, T);
B := BELOW(U, T);
IF A intersects L THEN
// Let q be the intersection of segments A and L;
INSERT(q, Q);
IF B intersects U THEN
// Let q be the intersection of segment B and U;
INSERT(q, Q);
END;에 선분들의 양 끝점을 넣는다. 에 들어 있는 점들은 축을 기준으로 오름차순을 유지하도록 한다.
지금 보고 있는 점 가 선분의 왼쪽 끝점인 경우 해당 선분을 에 넣고, 오른쪽 끝점인 경우 에서 제거한다. 를 지나는 선분을 에 넣거나 뺌으로써 새롭게 위아래 순서상 연속하게 되는 두 선분에 대해 교차 여부를 판정하고, 만약 두 선분이 서로 교차한다면 그 교점을 새로운 이벤트로 큐에 집어넣는다.
가 선분의 끝점이 아니라 교점인 경우에도 아이디어는 동일하다. 에서 교차하는 두 선분은 직전에 서로 순서상 연속하고 있다. 이때 위에 있던 것을 , 나머지를 이라 하자. 를 지나면서 두 선분의 순서는 서로 바뀌는데, 순서가 서로 바뀌더라도 를 지난 직후 서로 순서상 연속하는 것은 마찬가지다.
두 선분의 순서를 바꾸면, 이제는 이 위에 있고 가 아래에 있게 된다. 이때 은 자신의 바로 위에 있는 선분과 새롭게 순서상 연속하게 되고, 는 자신의 아래에 있는 선분과 새롭게 순서상 연속하게 된다. 따라서 그 각 선분쌍에 대해 교차 판정을 실시해보자. 만약 새롭게 연속하게 된 선분쌍이 서로 교차한다면 그 교차점도 다시 에 들어간다.
단, 에 교차 이벤트를 넣을 때에는 교점의 좌표가 이전에 확인했던 교차점이 아닌 경우에만 넣자. 이미 에 한 번 들어갔던 이벤트를 다시 넣을 필요는 없다.
각 이벤트를 처리하는 데 의 시간이 걸리고, 이벤트가 양끝점() + 교차점의 개수()만큼 있을 수 있으니 총 시간복잡도는 이다. 주의할 점은 교차점의 개수가 에 가까워진다면, 그냥 naive하게 모든 선분쌍을 비교하는 게 더 나을 수도 있다는 것이다.
(2) 예제
간단한 예제를 따라가 보면 좋을 것 같다.
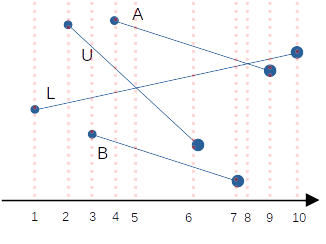
- 이 에 들어간다.
- 가 에 들어간다.
- 과 에 대해 교차 판정을 실시한다.
- 가 서로 교차하므로, 그 교차점을 에 넣는다(5에서의 이벤트).
- 가 에 들어간다.
- 와 에 대해 교차 판정을 실시한다.
- 교차하지 않으므로 다음으로 넘어간다.
- 가 에 들어간다.
- 에 대해 교차 판정을 실시한다.
- 교차하지 않으므로 다음으로 넘어간다.
- 의 교차 이벤트.
- 의 순서를 서로 바꾼다.
- 이제 이 와 연속하고 가 와 연속하게 됐으므로, 두 연속하는 선분쌍에 대해 교차 판정을 실시한다.
- 가 서로 교차하므로, 그 교차점을 에 넣는다(8번).
- 를 에서 제거한다.
- 에 대해 교차 판정을 실시한다.
- 교차하지 않으므로 다음으로 넘어간다.
- 를 에서 제거한다.
- 의 교차 이벤트.
- 의 순서를 서로 바꾼다.
- 를 에서 제거한다.
- 을 에서 제거한다.
3. 정당성 증명
혹시 위 알고리즘이 찾아내지 못하고 놓쳐버리는 교차점이 있을 수 있지도 않을까?
스위핑을 하면서 어떤 점을 지나쳐버린다는 것은 그 점이 에 들어가지 못했다는 것이다. 에 들어가지 못한 선분 교차점들이 있다고 가정하고, 그것들 중 가장 왼쪽에 있는 점을 라 하자.
의 왼쪽에서 일어난, 가장 오른쪽의 이벤트 지점(즉 선분 끝점, 혹은 교차점)을 라 하자. 가 에 들어가지 못한 교차점들 중 가장 왼쪽에 있는 점이므로, 보다 왼쪽에 있는 이벤트 지점은 에 들어갔던 적이 있다. sweep line이 를 지난 직후 다음의 두 경우를 생각해볼 수 있다.
- 를 지난 직후, 가 순서상 연속함
- 이 경우 에 대한 선분 교차 판정을 실시하고, 를 찾아 에 넣을 것이므로 는 확인된다(모순)
- 를 지난 직후, 가 순서상 연속하지 않음
- 를 지난 직후 가 순서상 연속하지 않는다면, 와 사이에 어떤 이벤트가 일어나 직전에는 가 순서상 연속하게 되어야 한다. 이는 가 이전의 마지막 이벤트 지점이라는 가정과 모순이다.
어떠한 경우에도 모순이 발생하므로 스위핑을 하면서 에 들어가지 못하는 선분 교차점은 존재하지 않는다.
4. 일반화
앞서 다음의 네 가지를 가정했다.
- 축에 수직인 선분은 없다.
- 세 선분이 한 점에서 만나는 경우는 없다.
- 서로 겹치는 선분도 없다(둘 이상의 점에서 서로 만나는 선분은 없다)
- 모든 이벤트 지점(즉 선분 끝점 및 선분 교차점)의 좌표는 서로 다르다.
1번의 경우 이전 글과 마찬가지의 방법으로 처리해주면 되고, 3번의 경우, 서로 겹치는 선분이 있으면 교점의 개수가 무한히 많아지므로 그대로 가지고 간다.
(1) 좌표가 같은 이벤트 지점이 있을 때
논의의 편의상 모든 이벤트 지점의 좌표가 서로 다르다는 가정을 했고, 때문에 앞서 pseudo-code의 이벤트 큐는 축을 기준으로 이벤트를 오름차순 정렬했다.
이벤트 지점을 지나는 sweep line을 전후로 선분들의 위아래 순서를 제대로 관리할 수만 있다면 각 이벤트 지점이 같은 좌표를 가져도 문제는 없다. 두 이벤트의 좌표가 같다면 좌표를 오름차순으로 되게 관리해, sweep line 전후의 선분 간 순서 관계를 제대로 유지할 수 있다.
한 sweep line에서의 모든 이벤트들을 처리한 후 선분의 위아래 순서 관계가 제대로 유지될 때, 정당성 증명은 위에서와 마찬가지로 진행할 수 있다.
(2) 한 점에서 셋 이상의 선분이 만나는 경우가 있을 때
크게 달라지는 건 없고, 한 점에서 셋 이상의 선분이 만나는 경우가 있다면 다음의 성질이
- 두 선분이 서로 교차한다면 반드시 두 선분이 순서상 서로 연속적(consecutive)으로 나타나는 수직선 가 존재한다(세 선분이 한 점에서 만나는 경우는 없다고 가정하는 경우).
다음과 같이 확장될 뿐이다.
- 점 에서 교차하는 선분들은 어떤 수직선 에서 순서상 연속적이다.
점 에서 몇 개의 선분이 만난다고 하자. sweep line이 를 지날 때에는 에서 교차하는 모든 선분들의 위아래가 뒤집힌다. 선분들의 순서를 뒤집고나면, 지금까지 해왔던 것과 같이 새롭게 생기는 연속 선분쌍들에 대해 교차 판정을 실시한다. 즉 에서 교차하는 선분 중 가장 위에 있는 선분과 바로 그 위의 선분, 그리고 에서 교차하는 선분 중 가장 아래에 있는 선분과 그 아래의 선분에 대해 선분 교차 판정을 실시한다.
5. 코드(C++)
백준 1266번 문제 "일어나!"의 소스 코드다. 서로 겹치는 선분이 없고, 세 선분이 한 점에서 만나는 경우가 없을 때 교점의 개수를 구하는 문제다. 정답이 100,000보다 작거나 같은 자연수임이 주어져있으므로, 의 시간복잡도로 풀 수 있다.
#include <iostream>
#include <vector>
#include <algorithm>
#include <queue>
#include <set>
#include <cmath>
#include <cassert>
using namespace std;
#define fastio cin.tie(NULL); cout.tie(NULL); ios_base::sync_with_stdio(false)
typedef double ld;
typedef pair<ld, ld> Point;
const ld EPSILON = 1e-6;
const int START = 0;
const int INTERSECT = 1;
const int END = 2;
Point operator*(const Point &p, const ld &d) { return { p.first * d, p.second * d}; }
Point operator-(const Point &p1, const Point &p2) { return Point(p1.first - p2.first, p1.second - p2.second); }
Point operator+(const Point &p1, const Point &p2) { return Point(p1.first + p2.first, p1.second + p2.second); }
ld operator*(const Point &p1, const Point &p2) { return p1.first * p2.second - p1.second * p2.first; }
int K;
ld cur;
bool after_intersection;
bool is_zero(ld d) {
return fabsl(d) < EPSILON;
}
struct Segment{
Point s;
Point e;
int idx;
ld slope;
Segment(Point _s, Point _e, int _idx) {
idx = _idx;
s = Point(K * _s.first - _s.second, _s.first + K * _s.second);
e = Point(K * _e.first - _e.second, _e.first + K * _e.second);
if (e < s) swap(s, e);
slope = (e.second - s.second) / (e.first - s.first);
}
ld eval() const {
return slope * (cur- s.first) + s.second;
}
bool operator<(const Segment& rhs) const {//위아래 순서
ld ev1 = eval();
ld ev2 = rhs.eval();
if (!is_zero(ev1 - ev2)) return ev1 < ev2;
if (slope != rhs.slope) return after_intersection ? slope < rhs.slope : rhs.slope < slope ;
return idx < rhs.idx;
}
Point operator*(const Segment& rhs) const {//교점 구하기
ld det = (e - s) * (rhs.e - rhs.s);
if (!det) {
if (e == rhs.s) return e;
return s;
}
return s + (e - s) * ((rhs.s - s) * (rhs.e - rhs.s)/det);
}
};
struct Event {
ld x;
ld y;
int type;
int idx1;
int idx2;
Event(Point p, int _type, int _idx) : x(p.first), y(p.second), type(_type), idx1(_idx), idx2(_idx) {}
Event(Point p, int _type, int _idx1, int _idx2) : x(p.first), y(p.second), type(_type), idx1(_idx1), idx2(_idx2) {}
bool operator<(const Event &e) const {
return tie(x, y, type) > tie(e.x, e.y, e.type);
}
};
int ccw(Point& a, Point& b, Point& c) {
ld ret = (b - a) * (c - b);
return is_zero(ret)? 0 : ret > 0 ? 1 : -1;
}
bool intersect(const Segment& seg1, const Segment& seg2) {
Point p1 = seg1.s, p2 = seg1.e;
Point p3 = seg2.s, p4 = seg2.e;
int p1p2 = ccw(p1, p2, p3) * ccw(p1, p2, p4);
int p3p4 = ccw(p3, p4, p1) * ccw(p3, p4, p2);
if (p1p2 == 0 && p3p4 == 0) {
if (p1 > p2) swap(p1, p2);
if (p3 > p4) swap(p3, p4);
return (p2 >= p3 && p4 >= p1);
}
return p1p2 <= 0 && p3p4 <= 0;
}
vector<Segment> segments;
priority_queue<Event> events;//Q
multiset<Segment> T;
set<pair<int, int>> ans;//서로 교차하는 선분쌍 집합
void push(Point &intersection, int idx1, int idx2) {
if (idx1 < idx2) swap(idx1, idx2);
if (ans.find({idx1, idx2}) != ans.end()) return;//이미 Q에 들어갔던 교차점인 경우는 다시 보지 않는다.
ans.insert({idx1, idx2});
Event e = Event(intersection, INTERSECT, idx1, idx2);
events.push(e);
}
void bentley_ottmann() {
for (auto &[s, e, idx, slope] : segments) {
events.push(Event(s, START, idx));
events.push(Event(e, END, idx));
}
while (!events.empty()) {
auto [x, y, type, idx1, idx2] = events.top();
events.pop();
cur = x;
if (type == START) {//INSERT
auto seg = segments[idx1];
auto it = T.insert(seg);
auto above = next(it);
auto below = prev(it);
if (above != T.end() && intersect(*above, *it)) {
Point intersection = (*above) * (*it);
push(intersection, it->idx, above->idx);
}
if (it != T.begin() && intersect(*below, *it)) {
Point intersection = (*below) * (*it);
push(intersection, it->idx, below->idx);
}
}
else if (type == END) {//ERASE
auto seg = segments[idx1];
auto it = T.lower_bound(seg);
auto above = next(it);
auto below = prev(it);
if (it != T.begin() && above != T.end() && intersect(*below, *above)) {
Point intersection = (*below) * (*above);
push(intersection, above->idx, below->idx);
}
T.erase(it);
}
else {//INTERSECT
auto seg1 = segments[idx1];
auto seg2 = segments[idx2];
if (is_zero(x - seg1.e.first) || is_zero(x - seg2.e.first)) continue;//끝점을 만난 경우
T.erase(seg1); T.erase(seg2);
//교차 이후 순서 바꾸기
after_intersection = true;
if (seg2.slope < seg1.slope) swap(seg1, seg2);
auto upper = T.insert(seg2);
auto lower = T.insert(seg1);
auto above = next(upper);
auto below = prev(lower);
if (above != T.end() && intersect(*upper, *above)) {
Point intersection = (*upper) * (*above);
push(intersection, upper->idx, above->idx);
}
if (lower != T.begin() && intersect(*lower, *below)) {
Point intersection = (*lower) * (*below);
push(intersection, lower->idx, below->idx);
}
after_intersection = false;
}
}
}
int main() {
fastio;
int N;
cin >> N;
vector<pair<Point, Point>> endpoints;
set<int> slopes;
for (int i = 0; i < N; i++) {
int x1, y1, x2, y2;
cin >> x1 >> y1 >> x2 >> y2;
endpoints.emplace_back(Point(x1, y1), Point(x2, y2));
if (x1 != x2) slopes.insert((y2 - y1) / (x2 - x1));
}
while (slopes.find(K) != slopes.end()) K++;
for (int i = 0; i < N; i++) segments.emplace_back(endpoints[i].first, endpoints[i].second, i);
bentley_ottmann();
cout << ans.size();
}
(1) 친절한 해설
main()
- 개 선분의 양 끝점을 입력받는다.
- 선분의 기울기를 계산해서
slopes에 넣어준다. 굳이 실수 자료형을 쓰지 않아도 적절한 를 찾을 수 있다. slopes에서 를 찾을 수 있는지 확인하면서 의 값을 계속 늘려간다. 어떠한 선분의 기울기와도 일치하지 않는 가 나타난다면, 가 새로운 축이 된다.- 를 찾았다면, 회전시킨 두 점을 양 끝점으로 가지는 선분들을 만든다.
struct Segment
- 양 끝점과 인덱스를 필드로 가지는 구조체다.
- 원래 평면 상에 있던 점 를 변환해서 넣어준다.
- 이 구조체는
multiset<Segment> T에 들어가 정렬된 채로 관리될 것이기 때문에, 정렬을 위해 연산자<를 오버로딩해준다. - 두 선분의 교점을 구하기 위해
*연산자를 정의해줬다. - 정렬 기준은 현재 훑어보고 있는 좌표
cur에서의 좌표다. 즉 두 선분 에 대해 이면 다.eval()을 통해 일 때의 좌표를 구해서 비교한다.
- 두 선분이 같은 좌표를 가지는 경우가 있을 수 있다. 이 경우 교차 이전에는 기울기를 기준으로 내림차순으로, 교차 이후에는 오름차순으로 정렬해 어떤 선분이 위에 있는지 확인한다.
- 기울기가 같은 두 선분이 서로 끝점에서 만나게 되는 경우가 있을 수 있다. 이 경우는 선분의
idx를 통해 정렬한다.
struct Event
- 선분을 자료구조 에 넣고 빼는 이벤트를 처리하기 위한 구조체다.
x, y는 이벤트 지점의 좌표,type은 0이면 삽입, 1이면 교차, 2면 삭제다.idx1, idx2는 교차 이벤트인 경우 어떤 선분이 교차하는지를 알기 위해 사용하며, 이 지점에서 교차하는 두 선분의 인덱스다. 교차 이벤트가 아닌 경우에는 동일한 값을 가진다.- 이벤트 정렬을 위한 비교함수도 추가한다. 값을 기준으로 정렬하되, 같은 에서 여러 이벤트가 일어날 수 있으므로
type과 값도 신경 써줘야 한다.- 아래의
priority_queue<Event> events가 이벤트를 관리한다.
- 아래의
bentley_ottmann()
- 각 선분들의 양끝점을 이벤트 큐에 넣어준다.
- 이때
cur은 현재의 sweep line이고, 그 아래는 앞의 pseudo-code와 동일하다. - 스위핑을 하면서 인접한 두 선분의 교차점이 이미 스윕했던 곳에 있을 수도 있다. 이 경우는 다시 볼 필요가 없으므로
push()에서 확인해 걸러준다. - 단 교차 이벤트에서 교차점이 어떤 선분의 오른쪽 끝점이 되는 경우에는 교차하는 두 선분의 순서를 서로 바꿔줄 필요가 없다. 해당 선분은 곧 이어 나올 삭제 이벤트에서 삭제될 것이다.
- 두 선분이 교차하고 나면, 기울기가 큰 선분이 위로 가게 된다. 위에 있는 선분과 그 위의 선분, 아래에 있는 선분과 그 아래의 선분에 대해 선분 교차 판정을 한다.
그 외
- 점을 표현하기 위해
Point(pair<double, double>)를 사용한다. 선분 교차 판정 및 교차점을 구하기 위한 연산자 오버로딩이 여럿 있다. - 선분 교차 판정은
intersect()와ccw()에서 진행한다. - 실수 자료형을 사용하고 있기 때문에 부동 소수점 오차가 발생한다.
- 부동 소수점 오차 없이 교점의 개수를 구하기 위해 서로 교차하는 선분쌍의 개수를 반환하게 했다. 셋 이상의 선분이 한 점에서 만나는 경우가 없으므로 가능하다.
Bentley and Ottmann, "Algorithms for Reporting and Counting Geometric Intersections," in IEEE Transactions on Computers, vol. C-28, no. 9, pp. 643-647, Sept. 1979, doi: 10.1109/TC.1979.1675432. (https://ieeexplore.ieee.org/document/1675432)
