[Algo] 샤모스-호이 알고리즘(Shamos-Hoey Algorithm)

Park Yeongseo·2024년 10월 21일

Shamos-Hoey 샤모스-호이 선분 교차 판정

Algorithm

목록 보기

14/19

1. Intro

아래의 문제를 보자.

D5 선분 교차 4: https://www.acmicpc.net/problem/20150

평면 상에 $N$ 개의 선분이 있을 때, 이 중 서로 교차하는 것이 있는지 확인하는 문제다.

나이브하게 생각하면 모든 선분들의 쌍을 비교하는 방식으로, $O(N ^ 2)$ 의 시간복잡도로 풀 수 있겠지만, 위 문제와 같이 $N$ 이 수 십만이 되면 당연히 쓸 수 없게 돼버린다.

샤모스-호이 알고리즘은 평면 상에 $N$ 개의 선분이 있을 때, 이 중 서로 교차하는 것이 있는지를 $O(N \log{N})$ 의 시간에 판별하는 알고리즘이다.

2. Inspiration

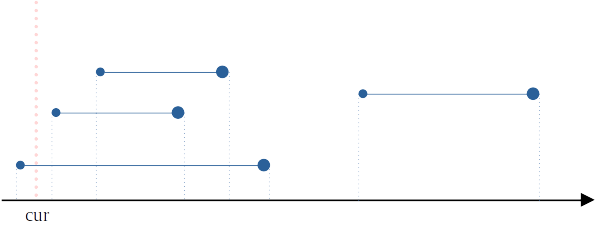
한 직선 위에 $N$ 개의 구간이 있고, 이 중 서로 겹치는 구간이 있는지를 물어보는 문제를 생각해보자. 이 문제는 각 구간의 쌍들을 비교하는 방식으로 $O(N^2)$ 에 해결할 수 있지만, 각 구간을 적절하게 정렬한다면, $O(N \log{N})$ 의 시간으로, 훨씬 더 빠르게 풀 수도 있다.

각 구간이 $[l, r]$ 과 같은 형식으로 주어진다고 해보자(단 $l \leq r$ 이고 $l, r \in \mathbb{R}$ ). 이 구간들을 왼쪽 끝점( $l$ )을 기준으로 오름차순으로, 만약 왼쪽 끝점이 같다면 오른쪽 끝점을 기준으로 오름차순으로 정렬하자.

현재 구간을 담을 수 있는 어떤 자료구조가 있다고 하자. 이제 맨 왼쪽에서 오른쪽으로 훑으면서, 왼쪽 끝점이 나오면 자료구조에 해당 구간을 넣고, 오른쪽 끝점이 나오면 해당 구간을 자료구조에서 뺀다. 만약 아직 자료구조에 어떤 구간이 담겨 있는데 새로운 왼쪽 끝점을 만나게 되면 두 구간이 겹친다는 의미다.

$2N$ 개의 끝점들을 정렬하는 데 $O(N\log{N})$ 의 시간이 걸리고, 정렬 후 $2N$ 개의 점을 모두 훑어보는 데에는 $O(N)$ 의 시간이, 자료구조에 구간을 넣고 빼는 데에는 $O(1)$ 의 시간이 걸리니, 시간복잡도는 $O(N\log{N})$ 이다.

(파란 선분들은 보기 쉽게 나타낸 것으로, 사실 모두 한 직선 위의 구간들이다.)

(1) 2차원 평면으로의 확장

위에서 1차원 직선 상 구간들을 정렬함으로써 $O(N^2)$ 의 시간복잡도를 $O(N\log{N})$ 으로 줄인 것처럼, 원래 문제였던 2차원 평면에서도 주어진 직선들을 어떻게 잘 정렬하면 $O(N^2)$ 의 시간복잡도를 $O(N\log{N})$ 으로 줄일 수 있다. 다만 앞서와 같이 단순히 양 끝점을 사전순으로 정렬하는 것으로는 문제를 풀 수 없고, 직선들에 다른 방법으로 순서를 매길 새로운 정렬 기준이 필요하다.

이제 2차원 평면에 $N$ 개의 선분들이 주어진다고 하자. 단, 일단은 다음을 가정한다.

$x$ 축에 수직인 선분은 없다.
세 선분이 한 점에서 만나는 경우는 없다.

평면 상에 있는, 두 선분 $A, B$ 에 대해 다음과 같은 관계를 정의하자.

def.

평면 상의 두 선분 $A, B$ 에 대해, 두 선분 모두와 교차하는 수직선 $x$ 가 존재하면, 두 선분은 $x$ 에서 비교가능(comparable)하다.

비교가능한 두 선분 $A, B$ 와 그때의 수직선 $x$ 에 대해, $A$ 와 $x$ 의 교점의 $y$ 좌표가 $B$ 와 $x$ 의 교점의 $y$ 좌표보다 크거나 같다면 $A$ 는 $x$ 에서 $B$ 보다 위에 있다고 하며, 다음과 같이 표기한다.
$A \uparrow_x B$

어떤 수직선 $x$ 에 대해, $x$ 와 교차하는 모든 선분들은 서로 비교가능하고, $\uparrow_x$ 는 추이성을 만족한다.

아래와 같이 선분들이 주어졌다고 하자.

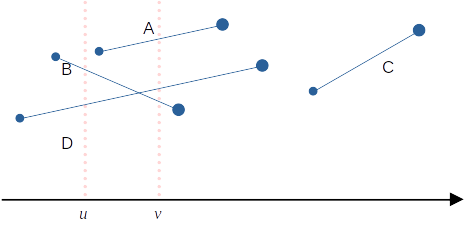
각 선분의 관계를 보면 $A$ 는 $B$ 와 $v$ 에서 비교가능하고, $A \uparrow_v B$ 다. $C$ 는 어떤 선분과도 비교가능하지 않다. $\uparrow_x$ 가 추이성을 만족하니, $D \uparrow_v B$ 이고 $A \uparrow_v D$ 이면 $A \uparrow_v B$ 임도 확인할 수 있다.

이제 맨 왼쪽에서부터 오른쪽으로 훑어 나가보자.

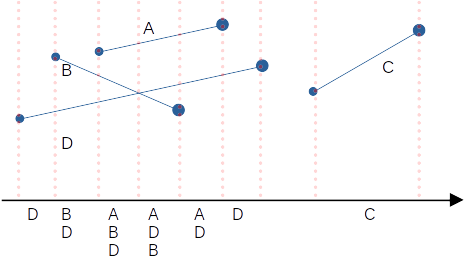
아래는 어떤 선분이 위에 있고 어떤 선분이 아래에 있는지를 나타낸다.

여기서 관찰할 수 있는 중요한 두 가지가 있다. 첫 번째는 교차하는 두 선분의 경우, 교차점을 기준으로 그 순서가 서로 바뀐다는 것이고, 두 번째는 두 선분이 서로 교차한다면 반드시 두 선분이 $\uparrow_X$ 순서상 서로 연속적(consecutive)으로 나타나는 수직선 $X$ 가 존재한다는 점이다(세 선분이 한 점에서 만나는 경우는 없다고 가정하는 경우).

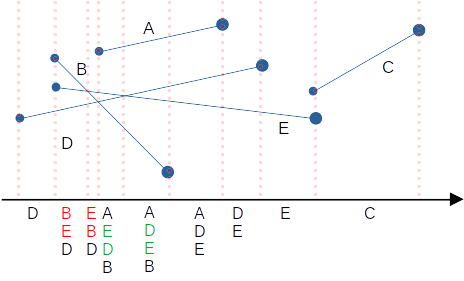
선분 $E$ 를 하나 더 추가하면 더 잘 보인다.

이제 우리가 해야할 일이 명확해지는데, 각 구간마다 위-아래 순서를 유지하면서 선분을 넣고 뺄 수 있는 자료구조를 마련하는 일이다.

다만 문제가 하나 있는데, 위와 같이 선분들의 순서가 바뀌는 지점을 알아내려면 각 교점들의 위치도 미리 알고 있어야 한다는 점이다. 교점들의 개수는 $O(N^2)$ 개가 되니, $N$ 개 선분의 교차 여부를 $O(N\log{N})$ 시간에 알아내고자 하는 목표에는 전혀 도움이 되지 않는다.

다행히 위의 두 번째, 두 선분이 서로 교차하면 반드시 두 선분이 $\uparrow_X$ 순서상 서로 연속적으로 나타나는 $X$ 가 존재한다는 점을 이용하면 각 교점들의 위치들을 모두 알지 못하더라도 $N$ 개의 선분 중 교차하는 것이 있는지의 여부를 빠르게 알 수 있다.

3. 샤모스-호이 알고리즘

각 선분들의 위-아래 순서를 유지하면서 선분을 넣고 뺄 수 있는 자료구조 $T$ 가 있다고 하자. 단 $T$ 를 통해 다음의 연산들을 수행할 수 있어야 한다.

i. INSERT(s, T): 선분 s를 T에 삽입한다.
ii. DELETE(s, T): T에서 선분 s를 삭제한다.
iii. ABOVE(s, T): T에 담긴 선분들 중 s 바로 위에 있는 선분을 반환한다.
iv. BELOW(s, T): T의 선분들 중 s 바로 아래에 있는 선분을 반환한다.

직선 상에서 $N$ 개 구간을 관리할 때와 마찬가지로, $2N$ 개의 끝점들을 왼쪽에서 오른쪽으로 정렬한 후, 맨 왼쪽에서 오른쪽으로 스위핑을 하면서 왼쪽 끝점을 만나면 $T$ 에 해당 선분을 삽입하고, 오른쪽 끝점을 만나면 $T$ 에서 해당 선분을 제거한다.

선분을 삽입하거나 제거할 때마다, 새롭게 순서상 연속이 되는 선분의 쌍이 생기게 되는데, 이 선분들이 서로 교차하는지를 확인하면 된다.

(1) Pseudo-code

SHAMOS-HOEY ALGORITHM (M.I.Shamos and D.Hoey, 1976를 일부 수정)

SORT the endpoints lexicographically on x and y so that POINT[1] is leftmost and POINT[2N] is rightmosts.

FOR I := UNTIL 2N DO BEGIN
	P := POINT[I] // Let S be the segment of which P is an endpoint.

	IF P is the left endpoint of S THEN BEGIN
		INSERT(S, T);
		A := ABOVE(S, T);
		B := BELOW(S, T);

		IF A intersects S THEN RETURN TRUE;
		IF B intersects S THEN RETURN TRUE;
	END;
	ELSE (P is the right endpoint of S) BEGIN
		A := ABOVE(S, T);
		B := BELOW(S, T);
		IF A intersects B THEN RETURN FALSE;
		DELETE(S, T);
	END;
	
END;

RETURN FALSE;

왼쪽 끝점을 만나면 해당 선분 $S$ 를 $T$ 에 넣는다. 이때 $S$ 는 바로 위에 있는 선분과 순서상 연속이 되고, 바로 아래에 있는 선분과도 순서상 연속이 된다. 위아래의 각 선분과 교차하는지를 확인하고, 만약 교차한다면 즉시 TRUE를 반환한다.

반대로, 오른쪽 끝점을 만나면 해당 선분 $S$ 를 $T$ 에서 빼야한다. $S$ 를 빼면 $S$ 의 바로 위에 있던 선분과 바로 아래에 있던 선분이 서로 순서상 연속하게 되므로, 그 두 선분이 서로 교차하는지를 확인한다. 교차한다면 즉시 TRUE를 반환하면 되고, 그렇지 않으면 $S$ 를 $T$ 에서 제거한 후 계속한다.

위 pseudo-code는 선분 교차가 감지되면 TRUE를 반환하기 때문에, 만약 TRUE가 반환됐다면 $N$ 개 선분들 중 교차하는 것이 적어도 하나 있음은 보장된다. 그런데 실제로는 선분 교차가 일어나지만 이를 찾아내지 못하는 경우가 있을 수도 있지 않을까?

(2) Theorem

2차원 평면상 $N$ 개의 선분들 중 서로 교차하는 것이 있다면, 위 알고리즘은 반드시 TRUE를 반환한다. (즉, 교차하는 선분이 있음에도 이를 찾아내지 못하는 경우는 없다.)

$pf.$
여러 개의 교차점들 중 가장 왼쪽에 있는 것, 만약 가장 왼쪽에 있는 것들이 여러 개라면 그 중 $y$ 좌표가 가장 작은 점을 $p$ 라고 하자.

$p$ 의 왼쪽 반평면에는 교차점이 없고 스위핑이 맨 왼쪽에서 오른쪽으로 이루어지므로, $p$ 까지 $T$ 에 담긴 선분들의 순서는 선분의 삽입 및 삭제가 일어날 때에만 바뀌게 된다. 다시 말해 $p$ 이전까지는 선분 교차로 인해 두 선분의 순서가 서로 바뀌는 일은 일어나지 않는다.

$p$ 에서 교차하는 두 선분을 $A, B$ 라고 하자. 두 선분이 교차한다면, 두 선분이 순서상 연속적으로 나타나게 되는 수직선 $X$ 가 존재한다. 그 수직선들 중 가장 왼쪽에 있는 것을 $x = q$ 라고 해보자. $x = q$ 에서 선분 $A, B$ 순서상 연속적이게 되는 경우는 두 가지 밖에 없다.

$x= q$ 에서 $A, B$ 사이에 있던 어떤 선분의 오른쪽 끝점이 나타나 $T$ 에서 삭제되는 경우.
또는 $x = q$ 에서 $A$ 나 $B$ 의 왼쪽 끝점이 나타나 $T$ 에 삽입되는 경우.

2번은 pseudo-code의 IF문에서, 1번은 ELSE문에서 캐치하게 되고, 때문에 위 알고리즘은 (교차점이 존재한다면) 점 $p$ 이전에, 적어도 점 $p$ 에 도달하는 시점에는 TRUE를 반환하게 된다.

위 코드는 TRUE, FALSE를 반환하게 변경했지만, 원래 코드에서는 교차하는 선분쌍을 반환하게 했다. 다만 이때 반환되는 선분쌍의 교점이 꼭 가장 왼쪽에 있는 교점은 아닐 수 있음에 주의.

4. 일반화

논의에 앞서 아래의 두 가지를 가정했었다.

$x$ 축에 수직인 선분은 없다.
세 선분이 한 점에서 만나는 경우는 없다.

만약 수직인 선분이 인풋으로 주어지거나, 세 선분이 한 점에서 만나는 경우도 존재한다면 처리해야할까?

(1) 수직인 선분이 있는 경우

수직인 선분이 있는 경우, 이것과 교차하는 선분들, 혹은 같은 $x$ 값을 가지는 다른 수직 선분과 이 선분을 어떻게 비교해야할지 문제가 생긴다.

수직 선분을 어떻게 따로 처리해주는 것도 가능하지만, 가장 간단한 방법은 축을 적절히 회전시켜 수직 선분이 존재하지 않도록 만드는 것이다.

보다 구체적으로는, 일단은 모든 선분의 기울기를 구한 후, 선분의 기울기와도 같지 않은 임의의 실수 $k$ 를 고르고, $y = 0$ 를 새로운 $y'$ 축으로 두면 된다.

구체적으로는, $y = kx$ 가 새로운 $y'$ 축이므로 새 $x'$ 축은 그에 수직인 $y = -\frac{1}{k}x$ 가 된다. $\theta = \arctan({-\frac{1}{k})}$ 일 때, 좌표계를 $\theta$ 만큼 회전시키자.

\begin {pmatrix} x'\\ y' \end {pmatrix} = \begin {pmatrix} \cos{\theta} & \sin{\theta} \\ -\sin{\theta} & \cos{\theta} \end {pmatrix} \begin {pmatrix} x\\ y \end {pmatrix}

이때

\begin {aligned} \cos{\theta} = \frac{k}{\sqrt{1 + k^2}} \\ \sin{\theta} = \frac{-1}{\sqrt{1 + k^2}} \end{aligned}

이므로 이를 대입하면 다음을 얻을 수 있다.

x'=\frac{kx-y}{\sqrt{k^2+1}}, y'=\frac{x+ky}{\sqrt{k^2+1}}

단 선분 교차 4 문제와 같이 모든 점들이 정수로 주어지는 경우, 정수 $k$ 를 찾고 $\sqrt{k^2 + 1}$ 를 곱해, $x' = kx - y, y' = x + ky$ 로 두더라도 선분 교차 여부를 판정하는 데에는 문제가 없다(부동소수점 오차가 없어지는 대신 오버플로우가 발생할 수 있음에 주의).

(2) 세 선분이 한 점에서 만나는 경우

점 $p$ 에서 셋 이상의 선분들이 교차하게 되는 경우는 어떨까? $p$ 에서 교차하는 여러 선분들 중, $p$ 직전의 어떤 점에서 순서상 연속하는 임의의 두 선분을 골라, 각각 선분 $A, B$ 라 한다면, 위에서의 논의를 그대로 적용할 수 있다.

5. 코드(C++)

#include <iostream>
#include <vector>
#include <algorithm>
#include <set>
using namespace std;

#define fastio cin.tie(NULL); cout.tie(NULL); ios_base::sync_with_stdio(false)
#define all(v) v.begin(), v.end()

typedef __int128 ll;
typedef pair<ll, ll> Point;

Point operator-(const Point& p1, const Point& p2) {
	return Point(p1.first - p2.first, p1.second - p2.second);
}

ll operator*(const Point& p1, const Point& p2) {
	return p1.first * p2.second - p1.second * p2.first;
}

ll K, cur;

struct Segment {
	Point s, e;
	int idx;

	Segment(Point _s, Point _e, int _idx) {
		s = Point(K * _s.first - _s.second, _s.first + K * _s.second);
		e = Point(K * _e.first - _e.second, _e.first + K * _e.second);
		idx = _idx;

		if (s > e) swap(s, e);
	}

	bool operator<(const Segment& rhs) const {
		auto &[x1, y1] = s;
		auto &[x2, y2] = e;
		auto &[x3, y3] = rhs.s;
		auto &[x4, y4] = rhs.e;

		ll eval1 = (y2 - y1) * (x4- x3) * (cur- x1) + y1 * (x2- x1) * (x4- x3);
		ll eval2 = (y4 - y3)* (x2- x1) * (cur- x3) + y3 * (x2- x1) * (x4- x3);

		if (eval1 != eval2) return eval1 < eval2;
		return idx < rhs.idx;
	}
};

struct Event {
	ll x;
	ll y;
	int val;
	int idx;

	Event(ll _x, ll _y, int _val, int _idx) : x(_x), y(_y), val(_val), idx(_idx) {} 

	bool operator<(const Event& e) {
		return tie(x, val, y, idx) < tie(e.x, e.val, e.y, e.idx);
	}
};

int ccw(Point& a, Point& b, Point& c) {
	ll ret = (b - a) * (c - b);

	return ret > 0 ? 1 : ret ? -1 : 0;
}

bool intersect(const Segment& seg1, const Segment& seg2){
	Point p1 = seg1.s, p2 = seg1.e;
	Point p3 = seg2.s, p4 = seg2.e;

	int p1p2 = ccw(p1, p2, p3) * ccw(p1, p2, p4);
	int p3p4 = ccw(p3, p4, p1) * ccw(p3, p4, p2);

	if (p1p2 == 0 && p3p4 == 0) {
		if (p1 > p2) swap(p1, p2);
		if (p3 > p4) swap(p3, p4);

		return (p2 >= p3 && p4 >= p1);
	}

	return p1p2 <= 0 && p3p4 <= 0;
}

vector<Event> events;
vector<Segment> segments;
multiset<Segment> T;

bool shamos_hoey() {
	for (auto &[s, e, idx] : segments) {
		events.emplace_back(s.first, s.second, 0, idx);
		events.emplace_back(e.first, e.second, 1, idx);
	}

	sort(all(events));

	for (auto &[x, y, val, idx] : events) {
		cur = x;
		if (!val) {//insert
			auto it = T.insert(segments[idx]);
			auto nxt = next(it);
			auto prv = prev(it);

			if (nxt != T.end() && intersect(*nxt, *it)) return true; 
			if (it != T.begin() && intersect(*prv, *it)) return true;
		}
		else {//erase
			auto it = T.lower_bound(segments[idx]);
			auto nxt = next(it);
			auto prv = prev(it);

			if (it != T.begin() && nxt != T.end() && intersect(*prv, *nxt)) return true; 
			T.erase(it);
		}
	}

	return false;
}

int main() {
	fastio;

	//N
	int N;
	cin >> N;

	vector<pair<Point, Point>> points;
	set<ll> slopes;

	for (int i = 0; i < N; i++) {
		int x1, y1, x2, y2;
		cin >> x1 >> y1 >> x2 >> y2;
		points.emplace_back(Point(x1, y1), Point(x2, y2));

		if (x1 != x2) slopes.insert((y2 - y1) / (x2 - x1));
	}

	while (slopes.find(K) != slopes.end()) K++;

	for (int i = 0; i < N; i++) {
		segments.emplace_back(points[i].first, points[i].second, i);
	}

	cout << shamos_hoey();
}

(1) 친절한 해설

`main()`

$N$ 개 선분의 양 끝점을 입력받는다.
선분의 기울기를 계산해서 slopes에 넣어준다. 굳이 실수 자료형을 쓰지 않아도 적절한 $k$ 를 찾을 수 있다.
slopes에서 $k$ 를 찾을 수 있는지 확인하면서 $k$ 의 값을 계속 늘려간다. 어떠한 선분의 기울기와도 일치하지 않는 $k$ 가 나타난다면, $y = kx$ 가 새로운 $y'$ 축이 된다.
$k$ 를 찾았다면, 회전시킨 두 점을 양 끝점으로 가지는 선분들을 만든다.

struct Segment

양 끝점과 인덱스를 필드로 가지는 구조체다.
원래 평면 상에 있던 점 $(x, y)$ 를 변환해서 넣어준다.
이 구조체는 multiset<Segment> T에 들어가 정렬된 채로 관리될 것이기 때문에, 정렬을 위해 연산자 <를 오버로딩해준다.
정렬 기준은 현재 훑어보고 있는 $x$ 좌표 cur에서의 $y$ 좌표다. 즉 두 선분 $A, B$ 에 대해 $A \uparrow_{cur} B$ 이면 $B < A$ 다.
- 혹시나 해서 각 선분들의 기울기의 분모를 모두 곱해 정수형으로 비교했지만, 그냥 선분들의 cur에서의 $y$ 좌표를 구해 실수형 변수에 넣어 비교해도 이 문제에서는 문제 없다.
단 두 선분이 cur에서 같은 $y$ 좌표를 가지는 경우가 있을 수 있으므로, 이때는 선분의 인덱스를 기준으로 정렬한다(어차피 바로 걸러지긴 한다).

struct Event

선분을 자료구조 $T$ 에 넣고 빼는 이벤트를 처리하기 위한 구조체다.
x, y는 선분 끝점의 좌표이고, val이 0이면 삽입, 1이면 삭제한다.
이벤트 정렬을 위한 비교함수도 추가한다. $x$ 순으로 스위핑을 해나갈 것이므로 $x$ 가 가장 먼저 온다. 각 $x$ 에서 양끝점에서 만나는 경우도 교차하는 것으로 판정하기에, 삭제는 삽입보다 나중에 이뤄져야 하므로 val을 다음으로 둬야 한다.

`shamos_hoey()`

각 선분들의 양끝점을 넣어준다.
이벤트를 정렬하고, 순차적으로 확인한다.
이때 cur은 현재의 sweep line이고, 그 아래는 앞의 pseudo-code와 동일하다.
multiset의 경우 insert가 iterator를 반환하기 때문에, 새로이 삽입한 선분의 위 아래에 어떤 선분이 있는지 바로 확인할 수 있다.

그 외

오버플로우가 일어날 수 있으므로 __int128 자료형을 사용한다.
점을 표현하기 위해 Point(pair<__int128, __int128>)를 사용한다. 선분 교차 판정을 위해 연산자 *를 두 벡터의 외적을 구하도록, -는 두 벡터의 차를 구하도록 오버로딩한다.
선분 교차 판정은 intersect()와 ccw()에서.

M. I. Shamos and D. Hoey, "Geometric intersection problems," 17th Annual Symposium on Foundations of Computer Science (sfcs 1976), Houston, TX, USA, 1976, pp. 208-215, doi: 10.1109/SFCS.1976.16.) (https://ieeexplore.ieee.org/document/4567905)

Park Yeongseo

이전 포스트

[Algo] 유량 네트워크 (2) 포드-풀커슨 방법 분석

다음 포스트