Introduction to Algorithm 4th edition을 번역 및 정리한 글입니다.
(2024.11.03) 파티 문제를 잘못 모델링해서 수정했습니다.

1. 유량 네트워크 (Flow networks)

유량 네트워크 $G = (V, E)$는 간선 $(u, v) \in E가$ 음이 아닌 용량(capacity) $c(u, v) \geq 0$을 가지고 있는 유향 그래프로, 특별한 두 개의 정점, 소스(source) $s$, 싱크(sink) $t$를 가진다. 단 여기에서 간선 $(u, v)$가 존재하는 경우, 그 역방향 간선 $(v, u)$는 존재하지 않아야 한다.

(1) 흐름(유량, flow)

위와 같은 네트워크 $G$에서 흐름 $f$는 다음의 두 성질을 만족하는 실수-값 함수 $f : V \times V \rightarrow \mathbb{R}$다.

(a) 용량 제한

모든 $u, v \in V$에 대해, $u$에서 $v$로 흐르는 흐름 $f(u, v)$는 다음을 만족해야 한다.

다시 말해, 한 정점에서 다른 정점으로의 흐름은 음이 아니며, 해당 간선의 용량을 초과하지 않는 값이어야 한다.

(b) 흐름 보존

모든 $u \in V - \{s, t\}$에 대해 다음을 만족한다.

즉 소스와 싱크를 제외한 모든 정점에 대해, 해당 정점으로 들어오는 흐름의 총합과 해당 정점에서 나가는 흐름의 총합은 동일해야 한다.

아래와 같은 유량 그래프가 있다고 생각해보자. 각 간선에 적힌 숫자는 해당 간선의 용량이다.

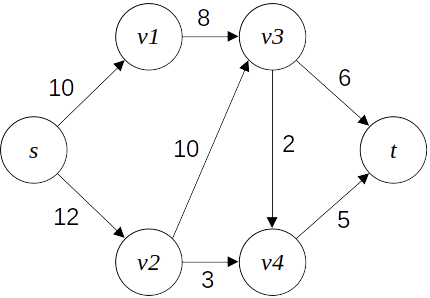
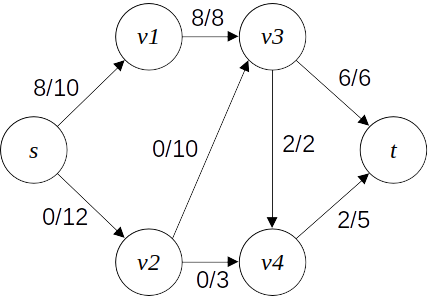
간선 $(s, v_1)$에 8의 유량을 흘려 보면 아래와 같이 흐르게 될 것이다. 각 간선에 적힌 $f/c$는 $c$의 용량을 가지고 있는 해당 간선에 $f$의 유량을 흘려 보냈음을 말한다.

2. 역평행 간선과 슈퍼 노드

(1) 역평행 간선(antiparallel edge)

앞서 유량 네트워크 $G = (V, E)$에 $(u, v)$라는 간선이 있으면 $(v, u)$라는 간선은 없어야 한다고 말했다. 이러한 간선 $(u, v)$와 $(v, u)$를 가리켜 역평행(antiparallel)하다고 말하는데, 만약 주어진 그래프에 역평행 간선이 존재하는 경우에는 어떻게 처리해야 할까?

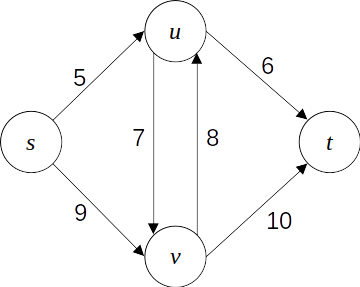
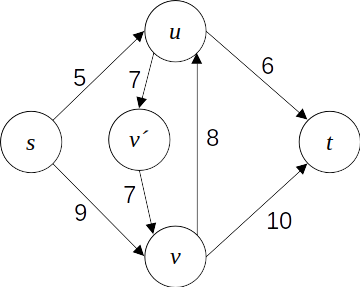
대충 위와 같이 역평행한 간선 $(u, v)$와 $(v, u)$가 모두 있는 경우, 아래와 같이 새로운 정점 $v'$를 추가해 역평행한 간선과 동치인 유량 네트워크를 모델링할 수 있다.

(2) 여러 개의 소스와 싱크를 가지는 경우

한편, 여러 개의 소스와 싱크가 존재하는 경우에는 어떻게 처리할 수 있을까?

다음과 같은 경우가 주어졌다고 해보자. 각각 세 개의 소스 $s1, s2, s3$와 싱크 $t1, t2, t3$가 있다(간선의 용량 표시는 생략).

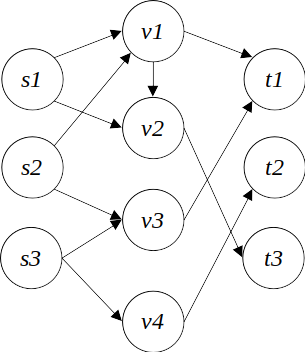
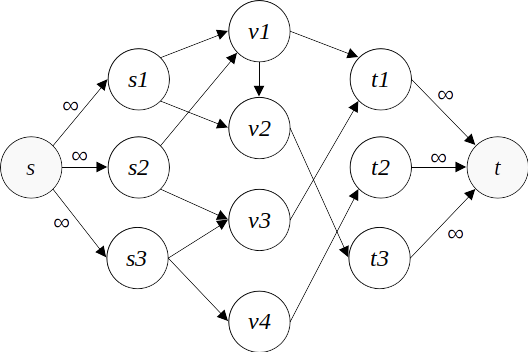
각 소스/싱크들과 연결된 새로운 소스 $s$, 싱크 $t$를 만들고, 무한한 용량의 간선으로 이어, 단일한 소스/싱크를 가질 수 있게 만들어 준다. 이렇게 만들어진 소스 $s$를 슈퍼소스(supersource), 싱크 $t$를 슈퍼싱크(supersink)라 한다.

3. 최대 유량 문제(maximum-flow problem)

흐름 $f$의 값 $|f|$는 다음과 같이 정의된다.

즉 유량 $f$의 값 $|f|$는 소스에서 나가는 흐름의 총합에서 소스로 들어오는 흐름의 총합을 뺀 것을 말한다. 최대 유량 문제는 소스 $s$, 싱크 $t$를 가지는 유량 네트워크 $G$에서, 이 값이 최대가 되는 흐름을 찾는 문제다.

위 유량 네트워크를 예로 보면 다음과 같이 $(s, v2)$에 추가로 3의 유량을 흘려 보냈을 때 최대 유량이 된다.

(1) 대표 문제

P4 파티: https://www.acmicpc.net/problem/2367

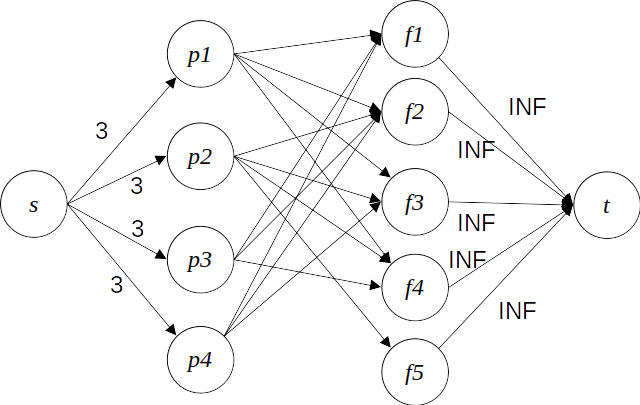
문제에서 주어진 예제 입력을 위와 같은 유량 네트워크로 모델링 할 수 있다.

한 사람이 최대 $K(=3)$ 접시의 음식을 준비할 수 있기에 간선 $(s, p_i)$의 용량을 3으로 두고, 한 사람이 준비할 수 있는 한 종류의 음식은 최대 한 접시이기에 $(p_i, f_j)$ 간선의 용량은 모두 1로 둔다.

이제 $s$에서 $f$로 흐르는 최대 유량을 찾으면 문제를 해결할 수 있다.

(2024.11.03) 각 음식에서 $t$로의 간선이 무한한 용량을 가지고 있는 것으로 그려놨지만, 문제를 다시 읽어보니 각 음식에도 최대 가져올 수 있는 접시의 수에 제한이 있었습니다. 때문에 해당 간선들의 용량은 무한이 아니라 음식 당 가져올 수 있는 접시의 수가 되어야 합니다.

4. Ford-Fulkerson method

포드-풀커슨 방법은 가장 간단하게 최대 유량을 찾기 위해 쓰이는 방법이다. 여기서 쓰이는 세 가지 주요 개념들이 있는데, 잔여 네트워크(residual network), 증가 경로(augmenting path), 컷(cut)이다.

기본적인 아이디어는 간단하다. 유량을 추가로 흘려 보낼 수 있는 경로가 없을 때까지 그런 경로가 있는지를 확인하고, 그런 경로가 있으면 유량을 흘려 보내는 것이다.

다음으로 넘어가기에 앞서 아래의 케이스를 생각해보자.

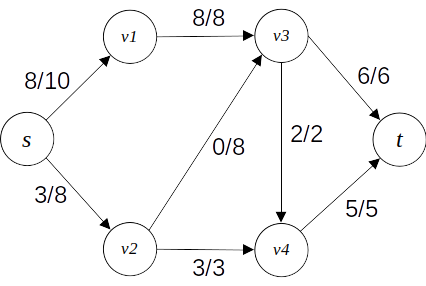
위 유량 네트워크에서 흐를 수 있는 최대 유량은 11이다.

그런데 아래와 같이 $(s, v2)$로 8의 유량이 흘렀다고 생각해보자.

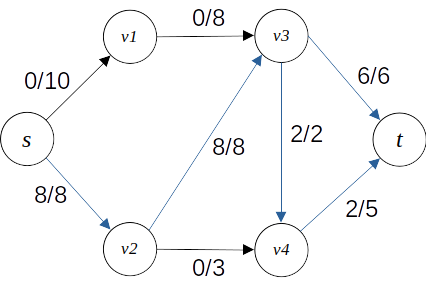
$(s, v2)$는 이미 가득 차 있으므로 더 이상 추가 유량을 흘려보낼 수 없고, $(s, v1)$으로 유량을 흘려보내도 이미 $(v3, v4), (v3, t)$의 용량이 가득 차 있기 때문에 추가적인 유량을 흘려보낼 수 없게 된다.

(1) Residual networks

(a) 잔여 용량(Residual Capacity)

유량 네트워크 $G$와 흐름 $f$가 주어졌다고 하자. 잔여 네트워크(residual network)는 이렇게 흐름을 보내고 남은 $G$의 간선의 용량을 자신의 간선의 용량으로 가지고 있는 네트워크다.

간단히, 용량 $c(u, v)$의 간선$(u, v)$에 유량 $f(u, v)$가 흐르고 있다면, 이 간선에는 $c(u, v) - f(u, v)$의 유량을 추가로 흘려보낼 수 있으므로, 해당 간선은 $G_f$에서 $c_f(u, v) = c(u, v) - f(u, v)$의 용량을 가지는 간선으로 추가된다.

그런데 위와 같이 이미 흐른 유량 때문에 더 이상 유량을 흘려 보낼 수 없게 되는 경우를 생각해보자. 이미 어떤 간선에 흐르는 유량은 줄이고 다른 곳의 유량을 높여 전체 유량을 증가할 수 있다면 위와 같은 문제를 해결할 수 있을 것이다.

이를 위해 잔여 네트워크에는 $G$에는 없던 다른 간선들도 추가되는데, $G$의 간선에 양의 유량 $f(u, v)$가 흐른다면, 잔여 네트워크 $G_f$에는 잔여 용량(residual capacity) $c_f(v, u) = f(u, v)$를 갖는 간선 $(v, u)$도 추가된다. 이렇게 역방향의 간선$(v, u)$으로 흐름을 보내는 것은 순방향 간선 $(u, v)$의 흐름을 줄이는 것으로 생각할 수 있고, 이를 통해 이미 간선$(u, v)$를 통해 흘려보낸 흐름을 줄이는 것이 가능해진다.

요컨대 소스 $s$, 싱크 $t$, 흐름 $f$를 가지고 있는 유량 네트워크 $G = (V, E)$에 대해, 잔여 용량 $c_f(u, v)$는 다음과 같이 정의할 수 있다.

앞서 제한하기를 유량 네트워크에 간선 $(u, v)$가 있으면 $(v, u)$는 없다고 했으니, 잔여 네트워크의 간선은 위 셋 중 하나만을 그 용량으로 가진다.

(b) 잔여 간선(Residual Edges)

위의 잔여 용량을 통해 잔여 네트워크 $G_f$는 다음과 같이 정의할 수 있다.

(b) 잔여 네트워크에서의 흐름

이 잔여 네트워크는 $(u, v)$와 $(v, u)$가 함께 존재할 수 있다는 점만을 제외하면 유량 네트워크와 동일한 성질을 가지고 있으며, 잔여 네트워크에서의 흐름은 원래 유량 네트워크에 흐름을 더하는 데에 로드맵을 제공한다.

$f$를 $G = (V, E)$의 흐름, $f'$를 $G$의 $f$에 대한 잔여 네트워크 $G_f$의 흐름이라고 하자. 이때 $f$를 $f'$만큼 증가(augmentation)시킨 것($f \uparrow f'$로 표기)은 다음과 같은 $V \times V \rightarrow \mathbb{R}$의 함수로 정의할 수 있다.

$G$에는 이미 $f(u, v)$가 흐르고 있다. 여기에 $f'(u, v)$를 더하는 것은 추가로 더 흘려보낼 수 있는 흐름을 흘려보내는 것이고, $f'(v, u)$를 빼는 것은 이미 흘려 보낸 유량을 그만큼 취소(cancellation)하는 것으로 볼 수 있다.

Lemma 1

$G = (V, E)$가 소스 $s$, 싱크 $t$를 가지는 유량 네트워크라 하고, $f$가 $G$의 흐름이라고 하자. $G_f$를 유량 네트워크 $G$의 $f$에 대한 잔여 네트워크라 하고, $f'$를 $G_f$의 흐름이라고 하자. 위에서 정의된 $f \uparrow f'$는 값 $|f \uparrow f'| = |f| + |f'|$를 가지는 $G$의 흐름이다.

$pf.$
우선 $f \uparrow f'$가 흐름의 첫 번째 성질(용량 제한)을 만족함을 보이도록 하자.

잔여 용량의 정의에 따라 $(u, v) \in E$이면 $c_f(v, u) = f(u, v)$이다. $f'$가 $G_f$의 흐름이므로, $f'(v, u)$는 $c_f(v, u)$를 초과할 수 없고, 따라서 $f'(v, u) \leq c_f(v, u) = f(u, v)$다. 그러므로

이다.

또한 흐름은 음이 아니고, 간선의 용량을 넘을 수 없음을 생각하면

이다.

따라서 $f \uparrow f'$ 는 $0 \leq (f \uparrow f')(u,v) \leq c(u,v)$로, 흐름의 첫 번째 성질을 만족한다.

다음으로는 $f \uparrow f'$가 흐름의 두 번째 성질(흐름 보존)을 만족하면서 $|f \uparrow f'| = |f| + |f'|$임을 보이자.

모든 $u \in V$에 대해 다음이 성립한다.

이를 증명하기 위해, 어떤 고정된 정점 $u$에 대해 다음과 같이 두 집합을 정의해보자.

$G$에 간선 $(u, v)$와 $(v, u)$가 함께 있는 경우가 없기 때문에, $V_l(u) \cap V_e(u) = \emptyset$이고, $V_l(u) \cup V_e(u) \subseteq V$다.

이전에 나온 항등식을 다시 보자.

$(f \uparrow f')(u, v)$가 양수가 되는 경우는 $(u, v) \in E$일 때 밖에 없다. 반대로, $(f \uparrow f')(v, e)$가 양수가 되는 경우는 $(v, u) \in E$일 때 밖에 없다. (각각 그 외의 경우는 모두 0이므로)

따라서 위 항등식은 다음과 같이 쓸 수 있다.

이제 $u = s$라 하자. 아래와 같이 $| f \uparrow f'| = |f| + |f'|$임을 증명할 수 있다.

또한 위 항등식을 정리하면 모든 $u \in V - \{s, t\}$에 대해 다음이 성립함도 증명할 수 있다.

(2) Augmenting paths

유량 네트워크 $G = (V, E)$와 흐름 $f$가 주어졌을 때, 증가 경로(augmenting path) $p$는 잔여 네트워크 $G_f$의, $s$에서 $t$로의 단순 경로(simple path)다.

증가 경로 위의 간선 $(u, v)$에는 최대 $c_f(u, v)$의 유량이 흐를 수 있으며, 이 간선들의 용량 중 최솟값을 증가 경로의 잔여 용량이라고 한다.

Lemma 2

유량 네트워크 $G = (V, E)$와 흐름 $f$를 생각하자. $p$가 $G_f$의 증가 경로라 할 때, $f_p : V \times V \rightarrow \mathbb{R}$를 다음과 같이 정의하면, $f_p$는 $|f_p| = c_f(p) > 0$인 $G_f$의 흐름이다.

$f_p(u, v) \leq c_f(p) \leq c_f(u,v)$이므로 용량 제한은 만족한다(증가 경로의 잔여 용량).
$p$가 잔여 네트워크 $G_f$의, $s$에서 $t$로의 단순 경로이기에, $s, t$를 제외한 정점들로 들어오는 흐름은 정점을 지나 동일한 양으로 그대로 흘러나가게 되므로 흐름 보존도 만족된다.

$u = s$인 경우를 보면, $p$가 $s$에서 $t$로의 단순 경로이기에, $s$에서 나가는 간선은 $f_p(s, v) = c_f(p)$를 유량으로 갖는 간선 하나 뿐이고, $s$로 들어오는 간선은 존재하지 않는다. 따라서 $\sum_{v \in V}f_p(s, v) - \sum_{v \in V}f_p(v, s) = c_f(p) - 0 = c_f(p)$이다.

Corollary 1

$G = (V, E)$가 유량 네트워크고, $f$를 $G$의 흐름, $p$는 $G_f$에서의 증가 경로라 하자. $f_p$가 위에 정의된 것과 같고, $f$가 $f_p$만큼 증가하는 경우, 함수 $f \uparrow f_p$는 값 $|f \uparrow f_p| = |f| + |f_p| > |f|$을 가지는 $G$의 흐름이다.

$pf.$ Lemma 1과 2.

(3) Cuts of flow networks

포드-풀커슨 방법은 더 이상 증가 경로를 찾을 수 없을 때까지 증가 경로를 찾아 유량을 흘려보내는 방법을 사용하는데, 그렇다면 이 과정이 모두 종료됐을 때 최대 유량을 찾을 수 있음이 보장될까?

최대 유량-최소 컷 정리(max-flow min-cut theorem)에 따르면 유량 네트워크의 유량이 최대라는 것은 잔여 네트워크에 더 이상 증가 경로가 없다는 것과 동치가 된다.

이를 알아보기 위해 컷(cut)에 대해 알아보자.

유량 네트워크 $G = (V, E)$의 컷 $(S, T)$는 정점 집합 $V$를 $s \in S$, $t \in T$인 두 개의 집합 $S$와 $T$로 분할한 것이다.

$f$가 흐름일 때, $S$와 $T$를 가로지르는 net flow $f(S, T)$는 다음과 같이 정의된다.

이때 컷 $(S, T)$의 용량은 다음과 같이 정의된다.

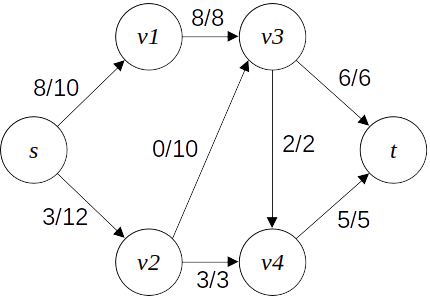
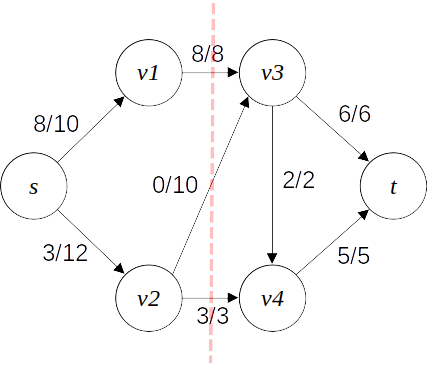
앞서 봤던 네트워크를 이렇게 잘라보자. $S = \{s, v1, v2\}, T = \{v3, v4, t\}$가 되도록 잘랐다.

이때 $f(S, T) = 8 + 0 + 3 = 11$ , $c(S, T) = 8+10+3 = 21$이다.

네트워크의 최소 컷(minimum cut)은 네트워크의 모든 컷들 중 최소의 용량을 가지는 것을 말한다.

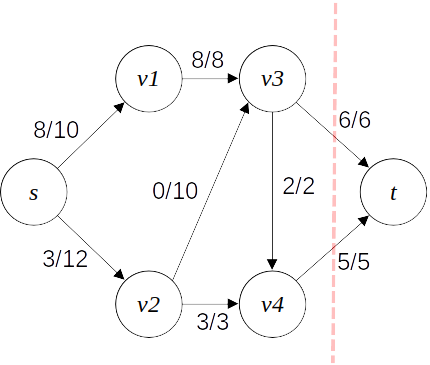
위 네트워크의 경우, 이렇게 $c(S, T) = 11$이 되도록 분할할 수 있고, 이것이 최소 컷이 된다.

Lemma 3

$f$가 소스 $s$, 싱크 $t$를 가지는 유량 네트워크 $G$의 흐름일 때, $G$의 임의의 컷 $(S, T)$에 대해 $(S, T)$를 가로지르는 net flow는 $f(S, T) = |f|$다.

$pf.$
$G$의 임의의 $u \in V - \{s,t\}$에 대해, 흐름 보존이 만족되므로 $|f|$는 다음과 같이 쓸 수 있다. 뒤쪽 괄호 안이 모두 0이 되기 때문이다.

위 항등식을 전개하고 다시 묶으면 다음을 얻을 수 있다.

$V = S \cup T$이고 $S \cap T = \emptyset$이므로 각 $\sum_{v \in V}$는 $\sum_{v\in S} 와 \sum_{v \in T}$의 합으로 나타낼 수 있다.

Corollary 2

네트워크 $G$의 임의의 흐름 $f$의 값은 $G$의 임의의 컷의 용량을 초과하지 못한다.

$pf.$
$(S, T)$를 $G$의 임의의 컷, $f$를 임의의 흐름이라 하자. Lemma 4와 용량 제한으로 인해

가 성립한다.

다만 이 따름정리는 $|f|$의 상한이 $c(S, T)$라고 말할 뿐이고, 아래의 최대 유량 최소 컷 정리에 따르면 사실 최대 유량은 최소 컷의 용량과 동일하다.

최대 유량 최소 컷 정리(Max-flow Min-cut Theorem)

$f$가 소스 $s$, 싱크 $t$를 가지는 유량 네트워크 $G = (V, E)$의 흐름이라 하자. 다음의 세 조건은 서로 동치다.
1. $f$가 $G$의 최대 유량이다.
2. 잔여 네트워크에 $G_f$ 증가 경로가 존재하지 않는다.
3. $G$의 어떤 컷 $(S, T)$에 대해, $|f| = c(S, T)$ 다.

$pf. (1) \Rightarrow (2) :$ $f$가 $G$의 최대 유량인데 $G_f$에 증가 경로 $p$가 존재한다고 하자. 만약 그렇다면 Corollary 1에 따라 $G$에는 $|f \uparrow f_p| > |f|$인 유량이 흐를 수 있다. $f$가 $G$의 최대 유량이라는 가정과 모순이므로 $f$가 최대 유량이면 $G_f$에 증가 경로는 존재하지 않는다.

$(2) \Rightarrow (3):$ $G_f$에 증가 경로가 없다고 하고, 다음과 같이 집합 $S, T$를 정의하자.

$G_f$에 증가 경로가 없으므로 $t \not\in S$고, 따라서 $t \in T$다.

$u \in S, v \in T$인 두 정점에 대해, $(u, v) \in E$가 있을 때, $f(u, v) = c(u, v)$다. 만약 $f(u, v) < c(u, v)$라면 남은 용량이 있어 $(u, v) \in E_f$가 되어 증가 경로에 포함되고, $s$에서 $v$로의 경로가 존재하기 때문이다.

만약 $(v, u) \in E$라면 $f(v, u) = 0$이 되어야 한다. 그렇지 않으면 $c_f(u, v) = f(v, u)$가 되어 $(u, v) \in E_f$가 되고, 마찬가지로 $v \in S$가 되기 때문이다.

따라서 다음과 같이 쓸 수 있다.

Lemma 3에 따라 $|f| = f(S, T) = c(S, T)$이다.

$(3) \Rightarrow (1) :$ Corollary 2에 따르면 임의의 컷 $(S, T)$에 대해 $|f| \leq c(S, T)$다. 따라서 어떤 컷에 대해 $|f| = c(S, T)$가 되는 것은 이 $f$가 최대 유량이라는 말이다.

5. 기본 Ford-Fulkerson

포드-풀커슨 방법에서는 반복적으로 증가 경로 $p$를 찾고, 이를 통해 유량 $f$를 값 $|f| + |f_p|$를 갖는 $f \uparrow f_p$로 바꾼다.

FORD-FULKERSON(G, s, t)
  for each edge $(u, v) \in G.E$
    $(u, v).f = 0$
  while there exists a path $p$ from $s$ to $t$ in the residual network $G_f$
    $c_f(p) = min\{c_f(u, v) : (u, v) \text{ is in } p\}$
    for each edge $(u, v)$ in $p$
      if $(u, v) \in G.E$
        $(u,v).f = (u, v).f + c_f(p)$
      else $(v, u).f = (v.u).f - c_f(p)$
return $f$

일단 모든 간선의 흐름을 0으로 초기화한 후, 잔여 네트워크 $G_f$에서 증가 경로를 찾는다. 증가 경로를 찾았다면 경로의 잔여 용량만큼 흐름을 추가로 흘려 보내주는데, 이때 간선이 $E$에 존재한다면 순방향이므로 흐름을 더해주고, 그렇지 않은 경우네는 역방향이므로 흐름을 빼준다.

더 이상 증가 경로를 찾을 수 없는 경우, 최대 유량을 찾은 것임을 증명했으므로 최대 유량인 $f$를 반환한다.

포드 풀커슨 방법에 대한 분석은 다음 글에