Introduction to Algorithm 4th edition을 번역 및 정리한 글입니다.

1. 다항식과 FFT

직관적으로 생각할 때, 차수가 $n$인 두 다항식을 더하는 데에는 $O(n)$, 곱하는 데에는 $O(n^2)$의 시간이 걸린다. 그런데 두 다항식을 곱하는 데 걸리는 시간을 $O(n\log n)$으로 줄이는 방법이 있으니, 바로 고속 푸리에 변환(fast Fourier transform, FFT) 이다.

(1) 다항식

대수적 수체 $F$의 변수 $x$에 대한 다항식은 함수 $A(x)$를 다음과 같이 합의 형식으로 표현한다.

여기서 값 $a_0,\ a_1,\ ...,\ a_{n-1}$은 다항식의 계수들이다. 계수와 $x$는 체 $F$에서 가져온다. 다항식 $A(x)$ 는 차수 $k$를 가지고 있다. 다항식은 가장 높은, 0이 아닌 계수가 $a_k$일 때 $k$ 차수라고 말하며, 다음과 같이 나타낸다.
$degree(A) = k$
어떤 다항식의 degree-bound가 $n$이라는 말은, 이 다항식의 차수가 $n$ 미만이라는 것이다. 즉 $0$ ~ $n-1$의 차수를 가지는 모든 다항식은 degree-bound가 $n$이라고 할 수 있다..

degree-bound가 $n$인 두 다항식 $A(x), B(x)$를 생각해보자. 두 다항식의 합 $C(x)$ 또한 degree-bound $n$이다.

한편, $A(x), B(x)$이 degree-bound $n$이라 할 때, 두 다항식의 곱 $C'(x)$는 degree-bound $2n-1$의 다항식이 된다.

만약 A의 차수가 $n_a$이고 B의 차수가 $n_b$이면 $C'$의 차수는 $n_a + n_b$이다. 다만 degree-bound가 $2n-1$인 다항식은 degree-bound $2n$이기도 하기에, 간단하게 다항식 곱의 degree-bound는 $2n$이라고 한다.

(2) 다항식의 표현

다항식은 여러 방식으로 표현할 수 있다.

(2-1) 계수 표현 (Coefficient representation)

다항식 $A(x) = \sum_{i=0}^{n-1}a_ix^i$ 는 다음과 같이 그 계수들을 모은 벡터로 표현할 수 있다.

점 $x_0$에서의 $A(x_0)$ 값을 계산하는 등의 연산은 계수 표현을 이용하면 간편하다. $A(x_0)$은 다음과 같이 $O(n)$의 시간에 계산할 수 있다(Horner's rule) .

두 다항식을 더하는 것도 $O(n)$ 시간에 가능하다.

하지만 단순히 두 다항식을 곱하는 건 $O(n^2)$ 시간이 걸린다. 벡터 $a$의 각 계수들(즉 다항식 $A(x)$의 계수들)을 벡터 $b$(다항식 $B(x)$의 계수들)에 있는 계수들에 각각 곱해줘야하기 때문이다.

(2-2) 점-값 표현 (Point-value representation)

degree-bound $n$인 다항식 $A(x)$은 $n$개의 point-value 쌍의 집합으로도 표현할 수 있다.

여기서 각 $x_k$들은 서로 다르며, $y_k = A(x_k)$를 만족한다.

하나의 다항식은 여러 p-v 표현을 가질 수 있는데, $n$개의 서로 다른 점 $x_0, ..., x_{n-1}$을 뽑아 $A(x_0), ..., A(x_{n-1})$을 계산하면 되기 때문이다..

앞서의 Horner's rule을 사용하는 경우 점 $x_k$에서의 값 $A(x_k)$는 $O(n)$에 계산할 수 있기에, $n$개의 점에 대한 값을 구해 p-v 표현을 만드는 경우의 시간복잡도는 $O(n^2)$이 될 것이다. 하지만 이 $x_k$들을 어떻게 잘 정하면 $O(n \log{n})$의 시간에 이를 계산할 수 있게 된다.

p-v 표현으로부터 역으로 다항식을 결정하는 것을 보간법(interpolation)이라 한다. 앞서 말했듯 한 다항식은 여러 p-v표현을 가질 수 있다. 하지만 $n$개의 점-값 쌍으로 이루어진 집합이 주어진 경우, degree-bound $n$인 다항식은 유일하게 결정될 수 있다.

(2-2.1)Th. Interpolating polynomial의 유일성

서로 다른 $x_k$에 대해, 집합 $\{(x_0, y_0), ..., (x_{n-1}, y_{n-1})\}$이 주어졌을 때, 각 $k = 0, 1, ..., n-1$에 대해 $y_k = A(x_k)$를 만족하는 degree-bound $n$의 다항식 $A(x)$는 유일하다.

$y_k = A(x_k)$는 위의 항등식과 동치다. 여기서 가장 왼쪽의 행렬을 방데르몽드 행렬(Vander-monde Matrix)이라 하며 $V(x_0, x_1, ..., x_{n-1})$로 표기한다.

방데르몽드 행렬의 행렬식은 $\prod_{j <k} (x_k - x_j)$이며, 따라서 각 $x_k$가 서로 다른 경우 $0$이 아닌 값이 된다. 즉 가역(invertible)이다.

이를 통해 우리는 다음과 같이 계수 행렬 $a$를 구할 수 있다.

p-v 표현을 이용하면 간편한 다항식 연산들이 있다.

degree-bound $n$의 다항식 $A(x), B(x)$가 있다고 하자.점 $x_0, ..., x_{n-1}$이 주어지고, 각 점에 대해 $A(x_k), B(x_k)$가 계산되어 있을 때, 그 $n$개의 같은 점에서의 다항식 합$C(x) = A(x) + B(x)$을 알고 싶다고 하자. $C(x_k) = A(x_k) + B(x_k)$이므로 $n$개 점의 값을 $O(n)$의 시간에 구할 수 있다.

p-v 표현을 이용하는 경우, 계수 표현과 달리, 다항식 곱의 경우도 마찬가지로 $C'(x) = A(x) B(x)$일 때, $C'(x_k) = A(x_k) B(x_k)$이므로 $n$개의 점에서의 다항식 곱의 값도 $O(n)$의 시간에 구할 수 있다.

우리의 목표는 두 다항식의 곱을 빠르게 구하는 것이었기에 p-v 표현을 쓰는 게 더 적절해보인다. 다만 $degree(C') = degree(A) + degree(B)$이므로 $A(x), B(x)$가 degree-bound $n$일 때, $C(x)$는 degree-bound $2n$이다. 우리가 계산을 통해 얻은 $C(x_k)$의 값들은 $n$개인데, 보간법을 이용해 $C(x)$를 알아내기 위해서는 적어도 $2n$개의 점이 필요하다. 어떻게 해야할까?

그냥 $2n$개의 점들로 시작하면 된다. $2n$개의 점 $x_0, ..., x_{2n-1}$에 대해 $A(x_k), B(x_k)$의 값을 찾아놓으면 된다.

$n$개의 각 $x_k$에 대해 $C(x_k) = A(x_k)B(x_k)$를 구하는 데에는 $O(2n) = O(n)$의 시간이 걸린다. $O(n^2)$보다 훨씬 빠르다.

(2-3) Fast multiplication of polynomials in coefficient form

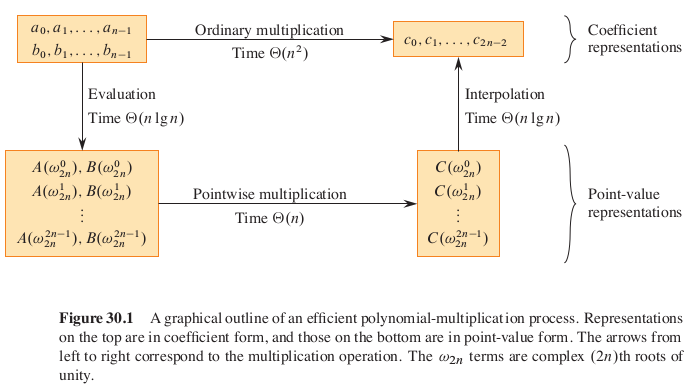
그렇다면 두 다항식의 계수들이 주어졌을 때, 어떻게 해야 둘의 곱을 빠르게 구할 수 있을까? 이는 계수 표현과 p-v 표현을 서로 얼마나 빠르게 변환할 수 있는지에 달려있다. 위 그림에서 볼 수 있듯, 계수 표현과 p-v 표현을 빠르게 변환할 수 있다면, 전체 시간복잡도는 $O(n\log{n})$이 될 수 있다.

앞서 말했듯, 보통 점 $x_k$에서의 값 $A(x_k)$는 $O(n)$에 계산될 수 있으므로, $n$개의 점에 대한 p-v 표현을 만드는 데에는 $O(n^2)$이 걸린다. 하지만 이 $x_k$들을 어떻게 잘 정하면 $O(n\log{n})$의 시간에 이를 계산할 수 있다.

전체 플로우는 정리하면 다음과 같다.
1. $A(x), B(x)$에 대한 degree-bound $2n$의 계수 표현을 만든다. 각 다항식의 차수보다 높은 차수에 계수가 $0$인 항들을 추가하면 된다.
2. $2n$개의 점에서의 $A(x), B(x)$ 값들을 계산한다.
3. $2n$개의 각 점에서 $A(x_k)$와 $B(x_k)$를 곱해 $C(x_k)$를 찾는다.
4. 보간법을 이용해 $C(x)$에 대한 계수 표현을 찾아낸다.

1번, 3번 단계는 $O(n)$, 2, 4번은 $O(n log{n})$의 시간이 걸려, 총 시간복잡도는 $O(nlog{n})$이 된다.

2. DFT와 FFT

(1) Complex roots of unity

1의 $n$제곱근(complex $n$th root of unity) $\omega$는 $\omega^n = 1$이 되는 복소수로, 정확히 $n$개가 있다($e^{2\pi i k/n}. k = 0, 1, ..., n-1)$.

$e^{iu} = \cos(u) + i \sin(u)$임을 생각해보자. $n$개의 1의 $n$제곱근들은 복소평면의 원점을 중심으로 하는 단위 원을 정확히 $n$등분하고 있는 것으로 생각할 수 있다.

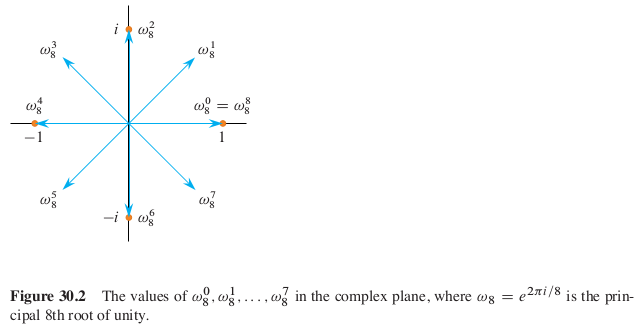
여기서 $\omega_n = e^{2 \pi i/n}$ 을 principal $n$th root of unity라 하며, 나머지는 $\omega_n$의 제곱꼴로 나타낼 수 있다. 즉 $n$개의 1의 $n$제곱근은 다음과 같다.

여기서 $\omega_n^n = \omega_n^0 = 1$이므로, $\omega_n^j \omega_n^k = \omega_n^{j+k} = \omega_n^{(j+k) \mod{n}}$임을 알 수 있다. 마찬가지로 $\omega_n^{-1} = \omega_n^{n-1}$이 된다. 아래의 보조 정리들은 1의 $n$제곱근이 갖는 몇 가지 기본적인 성질들이다.

(1-2) Cancellation Lemma

정수 $n >0, k \geq 0, d >0$에 대해, $\omega_{dn}^{dk} = \omega_n^k$다.

(1-2.1) 따름정리

짝수 $n > 0$에 대해, $\omega_n^{n/2} = \omega_2 = -1$이다.

(1-3) Halving Lemma

$n > 0$이 짝수일 때, $n$개의 1의 $n$ 거듭제곱근들을 제곱하면 $n/2$개의 1의 $n/2$ 거듭제곱근들을 얻을 수 있다.

Cancellation lemma에 의해 $0$이 아닌 정수 $k$에 대해 $(\omega_n^k)^2 = \omega_{n/2}^k$이다.

이므로 $(\omega_n^k)^2 = (\omega_n^{k + n/2})^2$이다.

이 렘마는 다항식의 계수 표현과 점-값 표현 변환을 $O(n \log{n})$에 할 수 있도록 하는 분할 정복을 위해 쓰인다.

(1-4) Summation Lemma

모든 정수 $n \geq 1$과 $n$으로 나누어지지 않는 $0$이 아닌 모든 정수 $k$에 대해,
$$ \sum_{j=0}^{n-1}(\omega _n^k)^j = 0$$> 이다.

등비수열의 합공식을 사용할 수 있다.

$n \not{|} k$이므로 $\omega_n^k \neq 1$이기에 가능하다.

(2) The DFT

degree-bound $n$인 다항식 $A(x) = \sum_{j = 0}^{n-1} a_j x_j$의 $\omega_n^0, ... , \omega_n^{n-1}$에서의 값을 계산한다.
$A$의 계수 표현은 $a = (a_0, a_1, ..., a_{n-1})$이다. $k = 0, 1, ..., n - 1$일 때, $y_k = A(\omega_n^k)$라 하자.

벡터 $y = (y_0, y_1, ..., y_{n-1})$을 계수 벡터 $a$의 DFT라고 하며, $y = DFT_n(a)$로 표기한다.

(3) The FFT

FFT는 직관적인 방법과 달리, 1의 거듭제곱근의 특별한 성질을 이용해 $O(n \log n)$의 시간에 $DFT_n(a)$를 계산한다. 다만 여기서는 $n$이 $2$의 제곱수라고 가정한다.

FFT는 분할 정복을 사용한다. 주어진 degree-bound $n$의 다항식 $A(x)$을 다음과 같이 두 개의 degree-bound $n/2$ 다항식으로 분할해보자.

즉 $A(x) = A^{even}(x^2) + xA^{odd}(x^2)$가 된다.

이제 $\omega_n^0, \omega_n^1, ..., \omega_n^{n-1}$에서의 $A(x)$ 값을 구하는 문제는 다음과 같은 문제로 줄어든다.

1. $n$개 점 $(\omega_n^0)^2, (\omega_n^1)^2, ..., (\omega_n^{n-1})^2$에서의 $A^{even}(x), A^{odd}(x)$ 값을 계산하고
   • Halving Lemma에서 봤듯 $n > 0$이 짝수일 때, $n$개의 1의 $n$ 거듭제곱근들을 제곱하면 $n/2$개의 1의 $n/2$ 거듭제곱근들을 얻을 수 있고, 각 $n/2$ 거듭제곱근들은 (부호만 바꿔서) 정확히 두 번 나타나게 되므로 $n$개의 점이 아니라 $n/2$개의 점에 대한 계산을 하게 된다.
2. 그 결과를 가지고 $A(x) = A^{even}(x^2) + xA^{odd}(x^2)$로 합치기

$A^{even}(x)$와 $A^{odd}(x)$에 대해서도 마찬가지의 방식으로 분할정복을 해나가면 된다. 재귀의 base case는 DFT를 실행할 원소가 하나 밖에 없을 때다. $y_0 = a_0 \omega_1^0 = a_0$이 되기 때문이다

FFT의 pseudo-code는 위와 같다. 길이를 계속해서 반으로 줄여가면서 가고 있기에 $O(n \log{n})$의 시간복잡도를 가짐을 바로 볼 수있다.

(3-1) Interpolation at the complex roots of unity

위와 같이 $O(n\log{n})$의 시간에 계수 표현에서 점-값 표현으로 변환했으니, 이번에는 보간법을 통해 점-값 표현에서 계수 표현으로 변환할 수 있기만 하면 된다.

DFT는 위와 같은 행렬 항등식으로 나타낼 수 있다. 여기의 방데르몽드 행렬 $V_n$의 역함수를 $y$에 곱해주면 계수 행렬 $a$를 얻을 수 있게 된다.

(3-2) Theorem

$j, k = 0, 1, ..., n-1$에 대해 , $V_n^{-1}$의 $(j,k)$ 성분은 $\omega_n^{-jk}/n$이다.

$V_n^{-1}V_n = I_n$임을 이용한다. $V_n^{-1}V_n$의 $(k, k')$ 성분은

$ $k'\neq k$이면 위 값은 0이고, $k = k'$이면 1이다. 사실 Summation Lemma에 따르면 $n \not{|} k' -k$
여야 하지만 $-n + 1 \leq k' -k \leq n - 1$이므로 $k \neq k'$만을 생각해도 좋다.

$V_n^{-1}$을 정의했으니 $DFT_n^{-1}(y)$는 다음과 같이 얻을 수 있다.

앞서 DFT에서 보았던 식과 아주 비슷하다. 때문에 비슷하게 FFT를 적절하게 변형하면 보간도 $O(n \log{n})$의 시간에 할 수 있게 된다.

Convolution Theorem

길이 $n$의 두 벡터 $a, b$에 대해, $n$이 $2$의 제곱수일 때,
$a \otimes b = DFT_{2n}^{-1}(DFT_{2n}(a) \cdot DFT_{2n}(b)$
다. 단 $a, b$는 길이가 $2n$이 되도록 0으로 패딩하고, $\cdot$은 벡터의 내적(dot product)이다.

3. Code

typedef complex<double> cpx;
const double PI = acos(-1);

vector<cpx> a, b;

/*
	계수 표현을 p-v 표현으로 변경하는 FFT
*/
void FFT(vector<cpx> &a, cpx omega_n) {
	int N = a.size();
	// base case. 아무 것도 하지 않는다.
	if (a.size() == 1) return; 

	// 홀수 차항, 짝수 차항을 나눈다
	vector<cpx> even(N / 2), odd(N / 2);

	for (int i = 0; i < N; i++) {
		if (i & 1) odd[i / 2] = a[i];
		else even[i / 2] = a[i];
	}

	// 각각에 대해 FFT. 분할 정복.
	// A(x) = A^{even}(x^2) + x * A^{odd}(x^2)
	FFT(even, omega_n * omega_n);
	FFT(odd, omega_n * omega_n);

	cpx omega(1, 0);

	// Halving Lemma.
	// 따름정리에 따라 w_n^{n/2 + k} = -w_n^k이므로
	for (int i = 0; i < N / 2; i++) {
		a[i] = even[i] + omega * odd[i];
		a[i + N / 2] = even[i] - omega * odd[i];
		omega *= omega_n;
	}
}

/*
	a와 b는 계수 표현이다.
	a[i] = A(x)의 i차 항의 계수, b[i] = B(x)의 i차 항의 계수
*/
vector<cpx> mult(vector<cpx> &a, vector<cpx> &b) {
	int N = 1;
	
	//두 다항식의 곱의 degree는 degree(a) + degree(b)다.
 	//2의 제곱수가 되도록 크기를 맞춰준다
	while (N < a.size() + b.size()) N <<= 1;
	
	a.resize(N); 
	b.resize(N);

	// principal nth root of unity
	double angle = 2 * PI / N;
	cpx omega_n = cpx(cos(angle), sin(angle));

	//두 계수 표현을 p-v 표현으로 변환한다
	FFT(a, omega_n);
	FFT(b, omega_n);

	//각 점에 대해 두 다항식의 곱의 값을 구한다.
	vector<cpx> res(N);
	for (int i = 0; i < N; i++) res[i] = a[i] * b[i];

	//역변환. 
	omega_n = cpx(cos(-angle), sin(-angle));
	FFT(res, omega_n);
	for (int i = 0; i < N; i++) res[i] /= N;

	return res;
}