다음과 같은 문제를 생각해보자.

$N$명의 사람과 $N$개의 작업이 있다. 모든 사람은 모든 작업을 할 수 있고, 각 사람이 각 작업을 마치는 데 드는 비용이 주어진다고 하자.

전체 비용을 최소(혹은 최대)로 하면서 $N$명의 사람과 $N$개의 작업을 1:1 매칭하려면 어떻게 해야할까?

위 문제를 좀 더 정식화해보자.

그래프 $G = (V, E)$가 정점 집합 $V$를 $L \cup R\ (\text{단 } |L| = |R| = N)$로 분할하는 완전 이분 그래프(complete bipartite graph)라 하자. 간선 $(l, r) \in E\ (l \in L, r \in R)$이 $w(l, r)$의 가중치를 가질 때, $G$의 완전 매칭(perfect matching) 중 간선 가중치의 총합이 최소(혹은 최대)가 되도록 하는 완전 매칭 $M^*$를 찾기.

• 완전 이분 그래프(complete bipartite graph): 정점 집합 $V$가 두 개의 독립적인 정점 집합 $L, R$로 분할될 때, $L$의 모든 정점이 $R$의 모든 정점과 간선을 가지는 그래프.
• 완전 매칭(perfect matching): 그래프의 모든 정점이 매칭되는 매칭.

가장 간단한 풀이는 모든 가능한 완전 매칭을 돌아보면서 가중치의 총합이 최소(혹은 최대)가 되는 것을 찾는 것이다. 이때, 가능한 완전 매칭의 수는 $N!$개이므로 그 시간복잡도도 $O(N!)$가 될 것이다.

오늘 다룰 헝가리안 알고리즘(Hungarian algorithm)은 훨씬 빠르게 $O(N^4)$, 최적화를 곁들이면 $O(N^3)$의 시간에 $M^*$를 찾는 알고리즘이다.

헝가리안 알고리즘을 이용하면 가능한 완전 매칭들 중 간선 가중치의 총합이 최소가 되는 것도, 최대가 되는 것도 찾을 수 있다.

다만 아래에서는 간선 가중치의 총합이 최대가 되는 것을 찾는 것을 목표로 한다.

1. 헝가리안 알고리즘

1.1. 이퀄리티 서브그래프(equality subgraph)

헝가리안 알고리즘에서는 주어진 완전 이분 그래프 $G$의 이퀄리티 서브그래프(equality subgraph)를 이용하며, 그 성질은 다음과 같다.

• 이퀄리티 서브그래프는 시간에 따라 변한다.
• 이퀄리티 서브그래프에서 찾은 완전 매칭은 주어진 할당 문제의 최적해임이 보장된다.

이퀄리티 서브그래프가 무엇인지 정의하기에 앞서, 각 정점에 새로운 속성값 $h$를 할당한다. 이 속성 $h$를 정점의 레이블(label)이라 부르며, 다음을 만족하는 $h$를 그래프 $G$의 허용 가능한 정점 레이블링(feasible vertex labeling)이라 한다.

허용 가능한 정점 레이블링은 항상 존재하며, 한 가지 기본적인 방법은

과 같은 초기값을 사용하는 것이다.

$def.$ 이퀄리티 서브그래프 (equality subgraph)

허용 가능한 정점 레이블링 $h$가 주어졌을 때, 그래프 $G = (V, E)$의 이퀄리티 서브그래프 $G_h = (V, E_h)$의 간선 집합 $E_h$는 다음과 같이 정의된다.
$E_h = \{(l, r) \in E: l.h + r.h = w(l, r)\}$

Theorem 1.

이퀄리티 서브 그래프 $G_h$에 완전 매칭 $M^*$가 있다면, $M^*$는 $G$의 할당 문제의 최적해이다.

$pf)$
$G_h$와 $G$가 같은 정점 집합을 가지고 있으므로, $G_h$에서 찾은 완전 매칭 $M^*$은 $G$의 완전 매칭이기도 하다.

(1) $M^*$의 모든 간선은 $G_h$의 간선이고, (2) 완전 매칭에서 각 정점은 모두 단 하나의 간선에만 나타나므로 다음이 성립한다.

$M$을 $G$의 임의의 완전 매칭이라 하자. (1) $h$가 허용 가능한 정점 레이블링이고, (2) $M$이 완전 매칭이므로 다음이 성립한다.

따라서 다음과 같이 쓸 수 있다.

즉 $G_h$의 완전 매칭의 $M^*$는 $G$의 최대-가중치 완전 매칭이다. $\square$

1.2. 이퀄리티 서브그래프의 완전 매칭 찾기

어떤 이퀄리티 서브그래프에서든 완전 매칭을 찾을 수 있다면, 그것이 바로 할당 문제의 최적해임이 증명됐다. 문제는 모든 이퀄리티 서브그래프에서 완전 매칭이 가능한 것은 아니라는 점이다. 따라서 우리는 우선 (1) 완전 매칭이 가능한 이퀄리티 서브그래프를 찾고, (2) 해당 그래프에서 완전 매칭을 찾아야 한다.

임의의 한 이퀄리티 서브그래프를 생각해보자. 이 서브그래프에서 찾을 수 있는 최대 매칭의 가중치 총합은 많아야 각 정점 레이블 값의 총합이다. 만약 정답에 해당하는 정점 레이블링이라면 그 정점 레이블의 총합은 $w(M^*)$의 값과 같아지고, 최대 매칭은 최대 가중치 완전 매칭이 된다.

헝가리안 알고리즘은 반복적으로 매칭과 정점 레이블을 수정함으로써, 완전 매칭을 찾을 수 있는 이퀄리티 서브그래프와 그 완전 매칭을 찾아낸다.

1. 이퀄리티 서브그래프 $G_h$에서, 임의의 허용 가능한 정점 레이블링 $h$와 매칭 $M$으로 시작한다.
2. $G_h$의 $M$-증가 경로 $P$를 찾고, 매칭을 $M \oplus P$로 업데이트해, 매칭 수를 증가시킨다.
3. 정점 레이블링을 수정해 이퀄리티 서브그래프를 업데이트한다.
4. 더 이상 $M$-증가 경로를 갖는 이퀄리티 서브그래프를 찾을 수 없을 때까지 2, 3을 반복한다.

정점 레이블링 초기값($l.h = max\{w(l,r): r \in R\} \text{ for all } r \in L, r.h = 0 \text{ for all } l \in R$)과, 가능한 임의의 매칭으로 시작한다(빈 매칭도 상관없다.).

(1) $G_h$에서 $M$-증가 경로 찾기

이퀄리티 서브그래프 $G_h$와 매칭 $M$이 주어졌다면, $G_h$로부터 다음을 만족하는 유향 이퀄리티 서브그래프(directed equality subgraph) $G_{M,h} = (V, E_{M, h})$를 만든다.

$M$-증가 경로는 아직 매칭되지 않은 $L$의 정점에서 시작해, 아직 매칭되지 않은 $R$의 정점으로 끝나는 경로다. $G_{M,h}$에서 찾은 $M$-증가 경로는 $G_h$의 $M$-증가 경로이기도 하므로 $G_{M,h}$에서 증가 경로를 찾을 수만 있으면 된다.

위와 같이 간선 집합을 만들면, 아직 매칭되지 않은 $L$의 정점들에서 시작해 아직 매칭되지 않은 $R$의 정점에 도달할 때까지 BFS를 계속한다. BFS를 진행하면 아직 매칭되지 않은 $L$의 정점을 각 트리의 루트로 갖는 너비-우선 포레스트(breadth-first forest) $F = (V_F, E_F)$가 만들어진다.

$M$-증가 경로가 $L$의 정점에서 시작해 $R$의 정점으로 끝나므로, 해당 경로에는 아직 매칭에 포함되지 않은 간선$(L \rightarrow R)$이 매칭에 포함된 간선($R \rightarrow L$)보다 반드시 1개 더 많아지게 된다.

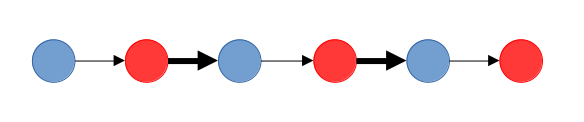
파란색은 $L$의 정점, 빨간색은 $R$의 정점을 나타낸다고 하자. 탐색을 통해 이와 같은 증가 경로를 찾았을 때, 굵은 화살표는 $R \rightarrow L$ 간선으로, 현재 매칭에 포함되어 있다.

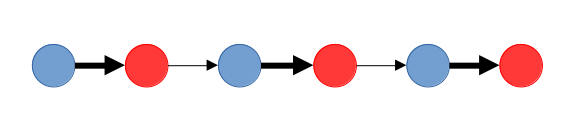
이를 거꾸로 뒤집어 $R \rightarrow L$ 간선(현재 매칭에 포함된 간선)은 매칭에서 제외시키고 $L \rightarrow R$ 간선(현재 매칭에 포함되지 않은 간선)은 매칭에 포함시키면, 위와 같이 기존보다 하나 더 많은 간선을 매칭에 포함시킬 수 있게 된다.

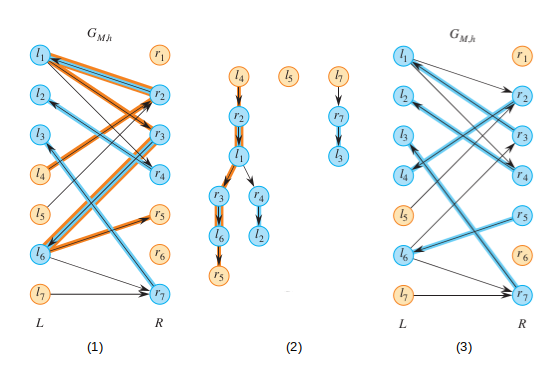
위 그림은 왼쪽에서부터 차례로

(1) 기존 매칭(파랑)으로부터 만들어 낸 유향 이퀄리티 서브그래프 $G_{M,h}$
(2) $G_{M,h}$에서 BFS를 통해 만들어 낸 BFS 포레스트와 $M$-증가 경로(주황)
(3) 찾아낸 $M$-증가 경로를 바탕으로 업데이트된 매칭(파랑)으로 새로 만든 $G_{M, h}$

에 해당한다.

(2) $M$-증가 경로 탐색이 실패하는 경우

$M$-증가 경로를 통해 매칭을 업데이트해 나가다 보면, 언젠가 해당 이퀄리티 서브그래프에서 더 이상 증가 경로를 찾을 수 없을 때를 만나게 된다. 이때의 매칭은 현재 이퀄리티 서브그래프에서 가능한 최대 매칭이기는 하지만, 완전 매칭은 아닐 수도 있다.

만약 이 매칭이 완전 매칭이 아니라면 증가 경로를 가진 다른 이퀄리티 서브그래프가 존재한다. 헝가리안 알고리즘에서는 증가 경로를 가진 다른 이퀄리티 서브그래프를 찾기 위해, 정점들의 레이블을 적절히 수정해 새로운 간선이 이퀄리티 서브그래프에 추가될 수 있도록 한다.

이때 염두에 둘 점은 증가 경로 탐색이 실패하는 경우의 탐색은 항상 $L$에 속하는 정점으로 끝난다는 점이다.

1. 가장 마지막에 탐색된 정점이 아직 매칭되지 않은 $R$의 정점이라면 $M$-증가 경로를 찾는 데 성공했다는 말이다.
2. 가장 마지막에 탐색된 정점이 이미 매칭된 $R$의 정점이라면 해당 정점과 매칭된 $L$ 정점으로 향하는 간선이 남아있을 것이므로 추가적인 탐색이 가능하다.
3. 따라서 증가 경로 탐색이 실패하는 경우는 $R$의 정점이 아닌 $L$의 정점으로 끝난다.

현재 BFS 탐색에서 도달하지 못한 $R$의 정점으로의 탐색이 가능하도록 간선을 추가해야 한다. 단 정점 레이블링 갱신은 다음의 세 조건을 만족해야 한다.

1. 어떤 $F$의 간선도 유향 이퀄리티 서브그래프에서 제외되지 않도록 해야 한다
   • 기존 탐색 결과를 유지하면서 추가적인 탐색이 가능해지도록 해야한다.
2. 어떤 $M$의 간선도 유향 이퀄리티 서브그래프에서 제외되지 않도록 해야 한다.
   • 기존 매칭 결과를 유지하면서 매칭을 더 증가시킬 수 있는 경로를 찾아야 한다.
3. $l \in L \cap V_F,\ r \in R - V_F$인 간선 $(l, r)$이 적어도 하나 $E_h$, $E_{M,h}$에 추가되도록 해야 한다.
   • 현재 상태로는 추가적인 탐색이 불가능하므로, 적어도 하나의 새로운 간선을 이퀄리티 서브그래프에 포함시켜야 한다.

이제 어떻게 해야 현재의 허용 가능한 정점 레이블링에서 아직 이퀄리티 서브그래프에 들어가지 못한 간선을 추가할 수 있을지를 생각해보자.

1. 지금 사용하고 있는 레이블링도 허용 가능한 정점 레이블링이므로 다음을 만족한다.
   $l.h + r.h \geq w(l,r) \text{ for all } l \in L \text{ and } r \in R.$
2. 이퀄리티 서브그래프의 정의에 따라 $l.h + r.h = w(l, r)$를 만족하는 간선 $(l, r)$은 이퀄리티 서브그래프에 포함된다.
3. 따라서 현재 이퀄리티 서브그래프에 포함되지 않은 간선의 양 끝 정점 $l, r$은 $l.h + r.h > w(l, r)$인 정점들이다.

만약 어떤 간선 $(l, r)$의 양 끝 정점의 레이블 값을 $l.h + r.h = w(l, r)$이 될 수 있도록 적절히 수정해줄 수 있다면, 이 간선을 이퀄리티 서브그래프에 포함시킬 수 있을 것이다.

물론 레이블 값을 임의로 수정하면 기존 $F$에 포함되어있던 간선들 중 일부가 그래프로부터 빠져나올 수도 있으므로 주의가 필요하다.

새 간선을 추가하기 위해 다음의 값 $\delta$를 계산하도록 하자. $F_L = L \cap V_F$고, $F_R = R \cap V_F$다.

$\delta$값을 찾았다면 모든 정점 $l \in F_L$과 $r \in F_R$의 레이블을 다음과 같이 수정한다.

Lemma

위와 같은 방식으로 레이블링 $h$를 $h'$로 수정할 때, $h'$는 다음의 성질을 만족하는 $G$의 허용 가능한 정점 레이블링이다.

1. $(u, v)$가 $G_{M,h}$의 포레스트 $F$에 속한 간선이면 $(u, v) \in E_{M, h'}$다. (탐색 유지)
2. $(l, r)$이 $G_h$의 매칭 $M$에 속한 간선이면 $(r, l) \in E_{M, h'}$다. (매칭 유지)
3. $(l, r) \not\in E_{M, h}$지만 $(l, r) \in E_{M, h'}$인 정점 $l \in F_L,\ r \in R - F_R$이 존재한다. (신규 간선)

$pf\ 0)$ $h'$가 허용 가능한 정점 레이블링임을 증명

현재의 $h$는 허용 가능한 정점 레이블링이므로, 모든 정점 $l \in L, r \in R$에 대해 $w(l, r) \leq l.h + r.h$다. 레이블링을 수정한 후의 $h'$가 허용 가능한 정점 레이블링이 아니라고 가정하자. 어떤 $l \in L, r \in R$에 대해, $l.h' +r.h' < w(l,r) \leq l.h +r.h$다.

이렇게 레이블링 수정 후 두 정점의 레이블 값의 합이 줄어들 수 었는 경우는 $l \in F_L, r \in R - F_R$일 때 밖에 없으며, 이때 수정된 레이블의 값은 $l.h' + r.h' = l.h + r.h - \delta$를 만족한다. 하지만 $\delta$ 값의 선정 방식에 따라, 모든 $l \in F_L, r \in R - F_R$에 대해 $l.h + r.h- \delta \geq w(l, r)$고, 따라서 $l.h' + r.h \geq w(l,r)$이다. 이는 $h'$가 허용 가능한 정점 레이블링이 아니라는 가정과 모순이므로 $h'$는 허용 가능한 정점 레이블링이다. $\square$

$pf\ 1)$ 성질 1 증명
$l \in F_L, r \in F_R$이라 하자. $l.h' + r.h' = (l.h - \delta) + (r.h + \delta) = l.h + r.h$이므로, 정점 $l, r$을 양 끝점으로 가지는 간선 $(l, r)$ 또는 $(r, l)$은 $G_{M, h'}$에도 포함된다. $\square$

$pf\ 2)$ 성질 2 증명
우선은 매칭 $M$에 포함된 임의의 간선 $(l ,r)$에 대해, $l \in F_L \Leftrightarrow r \in F_R$임을 증명한다.

우선은 $r \in F_R$이라 가정해보자. 앞서 증가 경로 발견에 실패하는 경우, BFS가 항상 $L$에 포함된 정점으로 끝남을 봤다. 따라서 만약 $r \in F_R$이면 해당 정점과 매칭되는 $l \in L$로의 탐색이 가능하고, 즉 $l \in F_L$이다. 이번에는 반대로 $r \not\in F_R$이라 가정해보자. $(l, r) \in M$이므로 $G_{M,h}$에서 $l$로 향하는 간선은 $(r, l)$밖에 없다. $r$로의 탐색에 실패했으므로 해당 간선을 따라 $l$로의 탐색을 하는 것은 불가능하다.

따라서 $(l, r) \in M$일 때 가능한 것은 $l \in F_L,\ r \in F_R$인 경우와 $l \in L - F_L,\ R \in R - F_R$인 경우, 두 가지 밖에 없다.

$l \in F_L,\ r \in F_R$인 경우, $l.h' + r.h' = l.h + r.h$다. 반대로 $l \in L - F_L,\ R \in R - F_R$인 경우도 마찬가지로, $l.h' = l.h,\ r.h' = r.h$이므로 $l.h' + r.h' = l.h + r.h$다. 따라서 $(l, r) \in M$이면 $(r, l) \in E_{M, h'}$다. $\square$

$pf\ 3)$ 성질 3 증명
$\delta$의 정의에 따라, $\delta = l.h + r.h - w(l,r)$이면서 $l \in F_L,\ r \in R - F_R$이 되는 간선 $(l, r) \not\in E_h$이 적어도 하나 존재한다. $l.h' + r.h' = l.h + r.h - \delta = w(l, r)$이므로 $(l, r) \in E_{h'}$다. $(l, r)$은 $E_h$에 포함되지 않으므로, 매칭 $M$에도 포함되지 않는다. 따라서 해당 간선이 유향 이퀄리티 서브그래프 $E_{M, h'}$에 들어갈 때 $L \rightarrow R$의 방향으로 들어가게 된다. 즉 $(l, r) \in E_{M, h'}$다. $\square$

2. Pseudo-code

헝가리안 알고리즘의 플로우를 다시 한 번 살펴보고 넘어가자.

1. 이퀄리티 서브그래프 $G_h$에서, 임의의 허용 가능한 정점 레이블링 $h$와 매칭 $M$으로 시작한다.
2. $G_h$의 $M$-증가 경로 $P$를 찾고, 매칭을 $M \oplus P$로 업데이트해, 매칭 수를 증가시킨다.
3. 정점 레이블링을 수정해 이퀄리티 서브그래프를 업데이트한다.
4. 더 이상 $M$-증가 경로를 갖는 이퀄리티 서브그래프를 찾을 수 없을 때까지 2, 3을 반복한다.

HUNGARIAN(G)

// 초기 정점 레이블링 설정
for each vertex l ∈ L
    l.h = max {w(l, r) | r ∈ R}
for each vertex r ∈ R
    r.h = 0
    
let M be any matching in G_h 

from G, M, and h, form the equality subgraph G_h 
	and the directed equality subgraph G_Mh

while M is not a perfect matching in G_h
    P = FIND-AUGMENTING-PATH(G_Mh)
    M = M ⊕ P
    update the equality subgraph G_h 
	    and the directed equality subgraph G_Mh

return M

아래의 FIND-AUGMENTING-PATH 프로시저는 HUNGARIAN 프로시저의 서브루틴으로, 증가 경로를 찾는 데 쓰인다. 여기서 $\pi$는 BFS 포레스트의 한 정점에 선행하는 정점을 가리킨다.

FIND-AUGMENTING-PATH(G_Mh)

Q = ∅
F_L = ∅
F_R = ∅

for each unmatched vertex l ∈ L
    l.π = NIL
    ENQUEUE(Q, l)
    F_L = F_L ∪ {l}
    
repeat
    if Q is empty
        δ = min { l.h + r.h - w(l, r) | l ∈ F_L and r ∈ R - F_R }
        
        for each vertex l ∈ F_L
            l.h = l.h - δ
        for each vertex r ∈ F_R
            r.h = r.h + δ

        from G, M, and h, form a new directed equality graph G_Mh
        
        for each new edge (l, r) in G_Mh
            if r ∉ F_R
                r.π = l
                
                if r is unmatched
                    an M-augmenting path has been found
                    (exit the repeat loop)
                else ENQUEUE(Q, r)
	                 F_R = F_R ∪ {r}
    
    u = DEQUEUE(Q)

	for each neighbor v of u in G_Mh
	    if v ∈ L
		    v.π = u
	        F_L = F_L ∪ {v}
	        ENQUEUE(Q, v)
	    elseif v ∉ F_R
			v.π = u
            if v is unmatched
                an M-augmenting path has been found
                    (exit the repeat loop)
            else ENQUEUE(Q, v)
                 F_R = F_R ∪ {v}
                 
until an M-augmenting path has been found

using the predecessor attributes π, construct an M-augmenting path P
	by tracing back from the unmatched vertex in R

return P

더 이상 해당 이퀄리티 서브그래프에서 $M$-증가 경로를 찾을 수 없는 경우 if Q is empty가 실행된다. Lemma의 (3)에 의해 if문을 거치면 적어도 하나 이상의 간선이 이퀄리티 서브그래프에 추가되므로, 큐가 비어 있어 if문 아래의 DEQUEUE(Q)가 실패하는 경우는 발생하지 않는다.

3. 시간복잡도 계산 및 개선

시간복잡도 계산 ($O(n^4)$)

주어진 이분 그래프 $G = (V = L \cup R, E)$에 대해, $|L| = |R| = n,\ |E| = n^2$라 하자.

우선 FIND-AUGMENTING-PATH 프로시저부터 보자.

1. 첫 번째 for 문은 $O(n)$의 시간에 완료될 수 있다.
2. repeat의 첫 번째 if문은 한 번 실행될 때마다 적어도 하나의 새로운 $R$의 정점을 찾으므로 최대 $n$번 반복될 수 있다.
   • (병목) δ 계산은 $O(n^2)$의 시간에 완료될 수 있다.
   • 정점 레이블 수정은 각각 $O(n)$의 시간에 완료될 수 있다.
   • (병목) 새로운 $G_{M,h}$ 구성은 $O(n^2)$의 시간에 완료될 수 있다.
   • $G_{M,h}$에 대한 for문의 경우 새롭게 추가될 수 있는 간선의 개수가 많아야 $n^2$개이므로, 한 번의 FIND-AUGMENTING-PATH 프로시저 호출에서 최대 $O(n^2)$번 실행된다.
3. 2.에서 다룬 if문을 제외한다면 repeat은 단순 BFS이므로 $O(V + E) = O(n^2)$의 시간에 완료될 수 있다.

따라서 FIND-AUGMENTING-PATH 프로시저의 시간복잡도는 $O(n^3)$다.

HUNGARIAN 프로시저의 경우,

1. 초기 정점 레이블링 설정은 $O(n ^2)$의 시간에 완료될 수 있다.
2. while 루프의 경우 매 루프마다 최소 하나의 매칭이 추가되므로, 최대 $n$번 수행될 수 있다.
   • while 조건문의 경우 상수 시간에 계산할 수 있다.
   • FIND-AUGMENTING-PATH는 $O(n^3)$의 시간에 완료될 수 있다.
   • 매칭 $M$의 업데이트는 $O(n)$의 시간에 완료될 수 있다.
   • $G_h$와 $G_{M,h}$의 업데이트는 $O(n^2)$의 시간에 완료될 수 있다.

따라서 HUNGARIAN 프로시저의 시간복잡도는 $O(n^4)$다.

시간복잡도 개선 ($O(n^3)$)

HUNGARIAN 프로시저의 시간복잡도가 $O(n^4)$가 되는 것은 FIND-AUGMENTING-PATH 프로시저에서 병목이 되는 $\delta$ 계산 및 $G_{M,h}$ 구성 때문이다. 이 둘의 시간복잡도를 각각 $O(n)$으로 개선할 수 있다면, FIND-AUGMENTING-PATH의 시간복잡도는 $O(n^2)$으로, HUNGARIAN의 시간복잡도는 $O(n^3)$으로 개선할 수 있다.

1. $\delta$ 값 계산의 $O(n)$의 시간 최적화
   원래는 $\delta$값 계산을 위해 모든 $(l, r)$ 정점 쌍의 레이블을 확인했기에 $O(n^2)$의 시간이 걸렸다. 하지만 이 과정은 다음과 같은 방식으로 $O(n)$으로 최적화할 수 있다.

   (1) 각 정점 $r \in R - F_R$에 대해, 다음의 새 속성값 $\sigma$를 정의한다. 이 $\sigma$는 보통 $r$의 슬랙(slack)이라고 부른다.
   $r.\sigma = min \{l.h + r.h - w(l,r) : l \in F_L\}.$

   이때 $\delta = min \{r.\sigma : r \in R - F_R\}$가 되므로, 만약 각 $r \in R - F_R$의 $\sigma$값이 계산되어 있다면 $\delta$ 또한 $O(n)$의 시간에 구할 수 있게 된다.

   (2) 계산된 $\delta$값을 가지고 각 정점들의 레이블 값을 수정한다. 이때 모든 $r \in R - F_R$에 대해 $r.\sigma$ 또한 $\delta$만큼 감소시켜줘야 한다. 모든 $r.\sigma$를 $r.\sigma - \delta$로 갱신해주는 데에는 $O(n)$의 시간으로 충분하다.

   (3) $F_L$에 새로운 정점 $l$이 추가되는 경우에도 모든 $r \in R - F_R$의 $\sigma$값을 수정해줘야 한다. $|L| = |R| = n$이므로 새로운 정점 $l$이 추가될 때마다 $O(n)$번의 $\sigma$값 수정이 일어날 수 있고, $F_L$에 새로 들어갈 수 있는 정점의 개수도 $O(n)$개다. 따라서 $F_L$ 계산에 따른 $\sigma$값 수정은 한 번의 FIND-AUGMENTING-PATH 프로시저에서 최대 $O(n^2)$번 수행될 수 있다.

2. 매번 $G_{M,h}$를 새로 만들지 않아도 된다.
   원래는 매 레이블링 갱신이 일어난 후, 어떤 간선이 $E_{M,h}$에 포함되는지 확인하기 위해 $O(n^2)$의 시간(=모든 간선을 확인하는 시간)을 들여 $G_{M,h}$를 새로 구성했지만, 사실 그럴 필요는 없다.
   

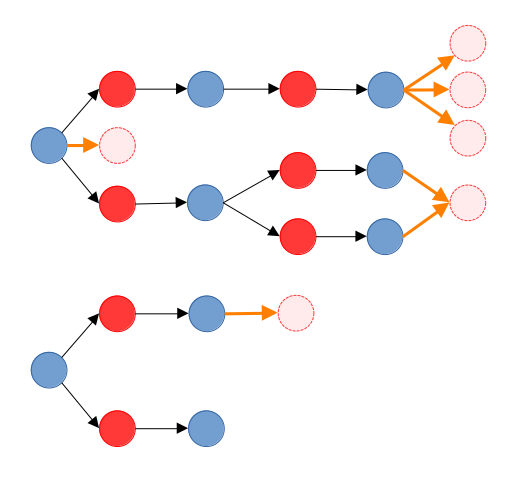
레이블링을 왜 수정했는지를 다시 생각해보자. 우리가 관심을 두는 것은 어떤 간선들이 실제로 $E_{M,h}$​에 포함될 것인지가 아니라, 어떻게 해야 포레스트를 확장하여 $M$-증가 경로를 찾을 수 있을지에 대한 것이다.

대충 위 그림을 통해 보자면, 레이블링 수정은 더 이상 탐색을 계속할 수 없는 포레스트 $F$에서, 아직 탐색되지 않은 $r \in R - F_R$로의 탐색을 가능하게 할 간선 후보들(주황 화살표)을 추가하기 위함이라 생각해도 좋다.

앞서 $\delta$ 값 계산 개선을 위해 사용했던 슬랙($\sigma$)을 이용하면 포레스트 $F$에 새롭게 추가될 수 있는 정점 및 간선도 보다 빠르게 찾을 수 있다.

(1) 레이블링과 슬랙을 수정한 시점에 $r.\sigma = 0$이 되는 정점 $r \in R - F_R$을 향하는 어떤 간선 $(l \in F_L,\ r)$이 $E_{M, h}$에 새롭게 추가된다. 이 시점에 $l.h + r.h = w(l, r)$이 되는 $(l, r)$쌍이 존재하게 되기 때문이다. 모든 $r$을 확인하는 데에는 $O(n)$의 시간이 걸린다.

(2) 만약 각 $r \in R - F_R$에 대해, $l.h + r.h - w(l,r) = r.\sigma$가 되는 $l$이 어떤 것인지도 추가로 관리해준다면, $E_{M,h}$에 추가되는 간선 $(l, r)$이 어떤 것인지도 $O(1)$에 알 수 있다. $F_L$에 새로운 원소가 들어갈 때, 각 $r$에 대해 $l.h + r.h - w(l,r) = r.\sigma$가 되도록 하는 $l$의 갱신도 $O(1)$에 해줄 수 있다.

원래는 매번 $F$에 추가할 수 있을 만한 간선을 찾기 위해 $O(n^2)$의 시간을 들였지만, 이제는 각 $r \in R - F_R$의 $\sigma$와 $l.h + r.h - w(l,r) = r.\sigma$가 되는 정점 $l$이 무엇인지만을 확인하면 되기 때문에 $O(n)$의 시간에 $F$에 간선을 추가할 수 있게 됐다.

4. 조금 다른 경우들

지금까지는 $|L| = |R| = n,\ |E| = n^2$인 경우의 최대 가중치 완전 매칭의 가중치를 찾으려 했지만, 조금만 수정한다면 $|L| \neq |R|$인 경우나, $|E| \neq n^2$인 경우의 매칭 최대 가중치, 혹은 최소 가중치 매칭을 찾는 경우도 해결할 수 있다.

1. $|L| \neq |R|,\ E = L \times R$ 인 경우
   더 작은 쪽에 더미 노드를 추가한 후, 다른 쪽의 모든 노드들과 $0$의 가중치를 갖는 간선으로 연결한다. $|L| \neq |R|$이므로 완전 매칭은 아니지만, 매칭의 최대 가중치는 올바르게 구할 수 있다.
2. $|L| = |R| = n,\ |E| < n^2$인 경우
   서로 연결되지 않은 노드들을 가중치 $0$의 간선으로 서로 연결한다. 마찬가지로 완전 매칭이 아닐 수 있고, 최대 매칭의 수를 구하지 못할 수도 있지만, 매칭 최대 가중치는 올바르게 구할 수 있다.
3. 최소 가중치 완전 매칭을 찾는 경우 ($|L| = |R| = n,\ |E| = n^2$를 가정)
   임의의 큰 값 $MAX$를 정하고 가중치를 $MAX - w(l, r)$로 수정한다. 이후 헝가리안 알고리즘을 수행해서 찾은 최대 가중치 완전 매칭의 가중치 $w(M^*)$을 $n * MAX$에서 빼주면 최소 가중치 완전 매칭이 된다. 더 간단하게는 그냥 모든 가중치 $w(l,r)$을 $-w(l,r)$로 수정하기만 해도 된다.

5. C++ 코드 (14216 할 일 정하기 2)

#include <iostream>
#include <vector>
#include <algorithm>
#include <climits>
#include <queue>
using namespace std;

#define fastio cin.tie(NULL); cout.tie(NULL); ios_base::sync_with_stdio(false)
#define all(v) v.begin(), v.end()

const int NIL = -1;
const bool LEFT = false;
const bool RIGHT = true;
const int MAX = 10000;

int N;
vector<int> rmatch, lmatch;
vector<int> l_pred, r_pred;
vector<vector<int>> w;
vector<int> lh, rh;

int find_augmenting_path() {//find augmenting path and return the index of an unmatched r, if any

	queue<pair<int, bool>> q;//{vertex idx, (0: left, 1: right)}
	vector<bool> FL(N), FR(N);
	vector<int> slack(N, INT_MAX), slack_l(N, NIL);

	for (int l = 0; l < N; l++) {
		if (lmatch[l] != NIL) continue;//unmatched l in L
		l_pred[l] = NIL;
		q.emplace(l, LEFT);
		FL[l] = true;
	}

	for (int l = 0; l < N; l++) {
		if (!FL[l]) continue;

		for (int r = 0; r < N; r++) {//none of R is in FR now
			if (lh[l] + rh[r] - w[l][r] < slack[r]) {
				slack[r] = lh[l] + rh[r] - w[l][r]; 
				if (slack[r] < 0) cout << lh[l] << "+" << rh[r] << "-" << w[l][r] << "=" << slack[r] << '\n';
				slack_l[r] = l;
			}
		}
	}


	while (true) {
		if (q.empty()) {
			int delta = INT_MAX;

			for (int r = 0; r < N; r++) {//optimize delta calculation with slack variable
				if (!FR[r]) delta = min(delta, slack[r]);
			}

			if (delta == INT_MAX) return -1;

			for (int i = 0; i < N; i++){
				if (FL[i]) lh[i] -= delta;

				if (FR[i]) rh[i] += delta;
			}

			for (int i = 0; i < N; i++) {
				if (FR[i]) continue;
					slack[i] -= delta;
					
					if (!slack[i]) {
						r_pred[i] = slack_l[i];

						if (rmatch[i] == NIL) return i;//unmatched
						q.emplace(i, RIGHT);
						FR[i] = true;
				}
			}
		}

		auto [u, V] = q.front();
		q.pop();

		if (V == RIGHT) {//matched right
			int l = rmatch[u];
			l_pred[l] = u;
			FL[l] = true;
			q.emplace(l, LEFT);

			for (int r = 0; r < N; r++) {
				if (!FR[r] && (slack[r] > lh[l] + rh[r] - w[l][r])) {
					slack[r] = lh[l] + rh[r] - w[l][r];
					slack_l[r] = l;
				}
			}
		}
		else {//left
			for (int r = 0; r < N; r++) {
				if ((rmatch[u] != r && lh[u] + rh[r] == w[u][r]) && !FR[r]) {
					r_pred[r] = u;

					if (rmatch[r] == NIL) return r;//unmatched
					q.emplace(r, RIGHT);
					FR[r] = true;
				}
			}
		}
	}
}

void update_match(int cur) {//backtrace augmenting path
	bool toggle = RIGHT;

	while (cur != NIL) {
		if (toggle == RIGHT) {
			rmatch[cur] = r_pred[cur];
			lmatch[r_pred[cur]] = cur;
			cur = r_pred[cur];
		}
		else cur = l_pred[cur];

		toggle = !toggle;
	}
}

int hungarian() {

	// default feasible vertex labeling
	for (int l = 0; l < N; l++) lh[l] = *max_element(all(w[l]));

	int max_match_weight = 0;

	while (true) {
		int r = find_augmenting_path();
		if (r < 0) break;
		update_match(r);
	}

	for (int l = 0; l < N; l++) {
		max_match_weight += w[l][lmatch[l]];
	}

	return max_match_weight;
};

void init() {
	w.assign(N, vector<int>(N));
	lh.resize(N);
	rh.resize(N);
	lmatch.resize(N, NIL);
	rmatch.resize(N, NIL);
	l_pred.resize(N, NIL);
	r_pred.resize(N, NIL);
}

int main() {
	fastio;

	cin >> N;

	init();

	for (int i = 0; i < N; i++) {
		for (int j = 0; j < N; j++) {
			cin >> w[i][j];
			w[i][j] = MAX - w[i][j];
		}
	}

	cout << N * MAX - hungarian();
}

Introdutction to Algorithms, 4th Edition