[Algo] 퍼시스턴트 세그먼트 트리(Persistent Segment Tree)

Park Yeongseo·2024년 11월 24일

Persistent Segment Tree 세그먼트 트리 자료구조 퍼시스턴트 세그먼트 트리

Algorithm

목록 보기

19/19

예전에 BOJ 11012 Egg 문제를 풀이하면서 대부분의 풀이가 퍼시스턴트 세그먼트 트리(Persistent Segment Tree)라는 자료구조를 사용하고 있다고 한 적이 있다.

1. Persistent Data Strcuture

어떤 자료 구조가 영속적(persistent)이라는 말은 수정이 일어날 때 자료 구조의 이전 버전을 유지해, 이후 해당 자료 구조의 옛 버전에 대한 접근을 가능케 한다는 말이다.

가장 간단한 예시로, 길이가 $N$ 인 (1차원) 정수 배열이 있고, 이 배열에 다음의 두 연산을 적용하려고 한다고 해보자.

시점 $t$ 에 배열의 $i$ 번째 원소의 값을 $v$ 로 변경한다.
시점 $t$ 에 배열의 $i$ 번째 원소의 값이 무엇이었는지를 반환한다.

이 두 가지 연산을 지원하는 자료 구조를 만드는 가장 간단한 방법은 당연히 아래와 같이 변경이 일어날 때마다 이전 상태를 전부 저장하는 것이다.

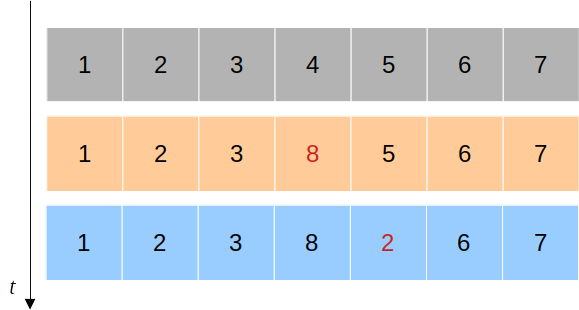
물론 이렇게 하면 수정이 일어날 때마다 상태를 복사하고 저장해야하기 때문에 시간에 있어서나, 메모리에 있어서나 너무 부담스러워진다. 어떻게 해야할까?

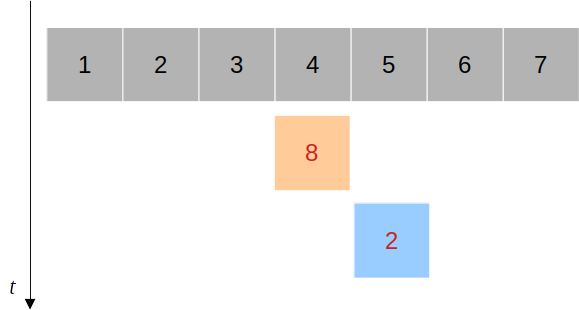
위와 같이 배열 전체를 저장하지 않고, 수정이 되는 부분(혹은 수정이 영향을 미치는 부분)만을 새로 만들어 저장하고, 자료 구조의 수정에 영향을 받지 않는 부분은 이전에 저장해놓은 것을 그대로 사용한다면 시간과 공간을 확연히 줄일 수 있다.

2. Persistent Segment Tree(PST)

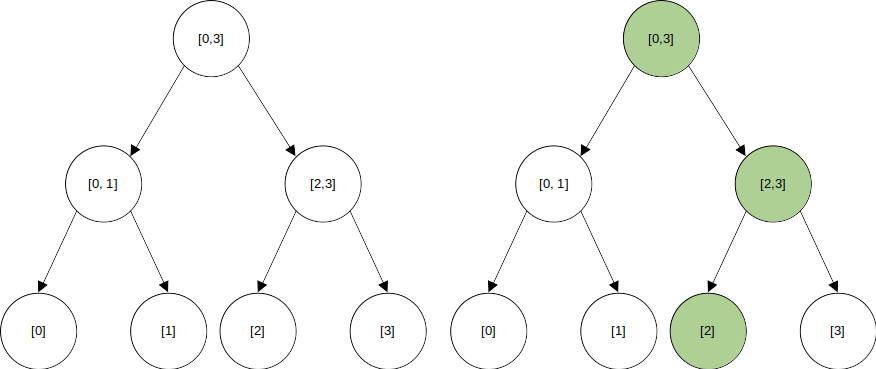
퍼시스턴트 세그먼트 트리도 위와 같은 1차원 배열과 크게 다를 게 없다. 대충 아래와 같은 세그먼트 트리가 있다고 하자.

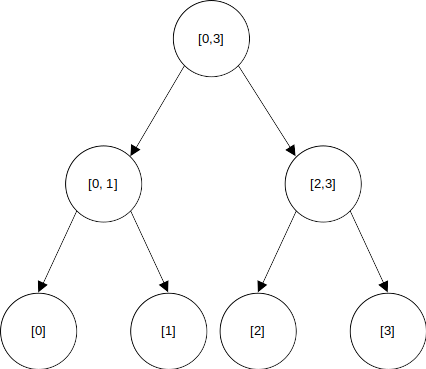
어떤 시점에 [2]에 수정이 일어난다고 해보자. 이렇게 포인트 업데이트를 하는 경우, 수정에 영향을 받는 노드는 $O(\log{N})$ 개로, 다음의 셋 뿐이다.

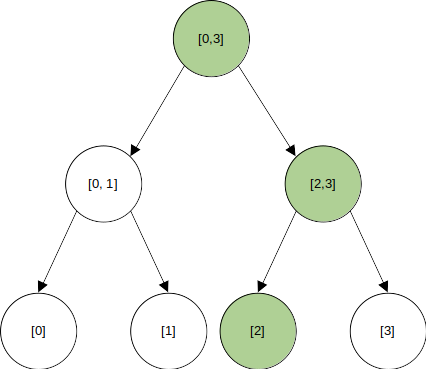
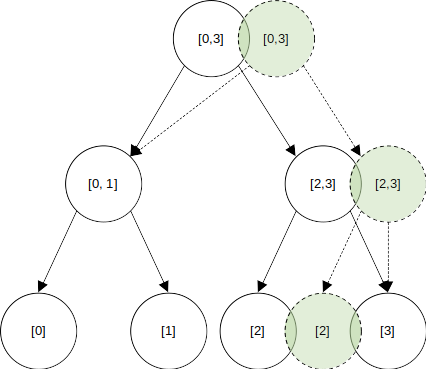
전체 세그먼트 트리를 복사한다면, 매 업데이트마다 $O(N)$ 개의 노드를 새로 만들어 줘야 하겠지만,

수정에 영향을 받지 않는 부분들은 그대로 두고, 수정되는 노드들만 새로 만들어준다면, 업데이트마다 $O(\log{N})$ 개의 노드만 새로 만들어주면 충분하다.

3. Dynamic Segment Tree

수정되는 노드들만 새로 만들어주려면 어떻게 해야할까?

보통 세그먼트 트리는 정적으로 선언되는 $O(N)$ 길이의 배열로 구현하는데, 만약 $N$ 이 너무 큰 데 비해 실제로 값이 들어가게 되는 노드는 그렇게 많지 않다면, 굳이 세그먼트 트리 전체를 만들어 이용하는 건 메모리 낭비다.

이러한 메모리 낭비를 막기 위해 업데이트가 일어나는 노드들만을 동적으로 만들어 세그먼트 트리를 구성할 수 있다. 이러한 방식을 동적 세그먼트 트리(Dynamic Segment Tree) 혹은 희소(?) 세그먼트 트리(Sparse Segment Tree)라고 부른다.

보통 동적 세그먼트 트리를 구현할 때에는 두 가지 방법이 있다고 말한다. 포인터를 이용하는 방법과 배열 & 인덱스를 이용하는 방법이다. 아래의 두 코드는 포인트 업데이트 & 구간 쿼리를 처리하는 구간합 세그먼트 트리를 구현한 것이다.

(1) 포인터를 이용한 동적 세그먼트 트리

struct Node {
	int val;
	Node *left, *right;

	Node() : val(0), left(NULL), right(NULL) {} 
};

struct Dynamic_Segtree {
	Node *root;

	Dynamic_Segtree() { root = new Node(); }

	void update(Node *node, int start, int end, int idx, int val) {
		if (start == end) {
			node->val = val;
			return;
		}

		int mid = (start + end) / 2;

		if (idx <= mid) {
			if (!node->left) node->left = new Node(); 
			update(node->left, start, mid, idx, val);
		}
		else {
			if (!node->right) node->right = new Node(); 
			update(node->right, mid + 1, end, idx, val);
		}

		node->val = (node->left ? node->left->val : 0) + (node->right ? node->right->val : 0);
	}

	int query(Node *node, int start, int end, int left, int right) {
		if (!node || right < start || end < left) return 0;
		if (left <= start && end <= right) return node->val;

		int mid = (start + end) / 2;

		return query(node->left, start, mid, left, right) + query(node->right, mid + 1, end, left, right);
	}
};

포인터를 이용한 구현의 경우, 각 노드에 좌우 자식 노드의 포인터가 들어있다.

아래의 배열과 인덱스를 통한 구현보다는 좀 더 간단하고 편하지만, 64비트 주소 체계에서 포인터는 8바이트의 크기를 가지기 때문에, 하나의 노드가 차지하는 공간이 좀 더 커질 수 있다는 단점이 있다(위의 경우 노드 하나가 24바이트의 크기를 가짐). 메모리 제한이 빡빡한 경우에는 사용하기 힘들 수도 있다.

new를 통해서 노드를 동적 할당하기 때문에 여러 개의 테스트 케이스가 있는 문제의 경우 메모리 해제에도 신경을 써줘야 한다.

(2) 배열과 인덱스를 이용한 동적 세그먼트 트리

struct Node {
	int val;
	int left, right;

	Node() : val(0), left(-1), right(-1) {} 
};

struct Dynamic_Segtree {
	vector<Node> nodes;//nodes[0] is a root node

	Dynamic_Segtree() { nodes.emplace_back(); }

	void update(int node, int start, int end, int idx, int val) {
		if (start == end) {
			nodes[node].val = val;
			return;
		}

		int mid = (start + end) / 2;

		if (idx <= mid) {
			if (nodes[node].left < 0) {
				nodes.emplace_back();
				nodes[node].left = nodes.size() - 1;
			}; 
			update(nodes[node].left, start, mid, idx, val);
		}
		else {
			if (nodes[node].right < 0) {
				nodes.emplace_back();
				nodes[node].right = nodes.size() - 1;
			}; 

			update(nodes[node].right, mid + 1, end, idx, val);
		}

		nodes[node].val = (nodes[node].left < 0 ? 0 : nodes[nodes[node].left].val) + (nodes[node].right < 0 ? 0 : nodes[nodes[node].right].val);
	}

	int query(int node, int start, int end, int left, int right) {
		if (node < 0 || right < start || end < left) return 0;
		if (left <= start && end <= right) return nodes[node].val; 

		int mid = (start + end) / 2;

		return query(nodes[node].left, start, mid, left, right) + query(nodes[node].right, mid + 1, end, left, right);
	}
};

배열과 인덱스를 이용한 구현의 경우 좌우 자식 노드의 인덱스만을 저장하면 되기 때문에 포인터를 통한 구현보다는 메모리를 절약할 수 있다. 위의 경우 하나의 노드가 12 바이트의 크기를 가진다.

다만 계속해서 emplace_back()으로 새로운 노드를 추가하고 있기 때문에, 적당한 크기의 메모리를 미리 reserve()로 확보해놓지 않으면 노드가 추가됨에 따라 추가적인 오버헤드가 발생할 수 있다(capacity가 가득 찼을 때의 vector원소 복사 시간. c++의 vector 메모리 할당 방식에 따른 추가적인 메모리 사용 등).

4. 구현

이제 퍼시스턴트 세그먼트 트리를 구현해보자. 길이가 $N$ (최대 $100,000$ )인 1차원 배열에 대한 포인트 쿼리 & 구간 쿼리를 처리하는 세그먼트 트리다.

struct Node {
	int val;
	int left, right;

	Node() : val(0), left(-1), right(-1) {} 

	Node(const Node &node) {
		val = node.val;
		left = node.left;
		right = node.right;
	}
};

struct PST{
	int N;
	vector<Node> nodes;
	vector<int> root;

	PST(int N, int Q): N(N) { 
		nodes.reserve(4 * N + 18 * Q);//초기 세그먼트 트리를 위한 공간 + log(N) * 업데이트 횟수만큼의 공간을 미리 확보 
		root.reserve(Q + 1);//초기 세그먼트 트리의 루트 노드 인덱스 = root[0], 이후 i(1 <= i <= Q)번째 업데이트의 루트 노드 인덱스는 root[i]
	}

	//노드 복사 및 생성
	int copy_node(const Node& node) {//기존의 노드를 복사해 그 인덱스를 반환
		nodes.emplace_back(node);
		return nodes.size() - 1;
	}

	int make_node() {//새로운 노드를 만들어 인덱스를 반환
		nodes.emplace_back();
		return nodes.size() - 1;
	}

	//초기 배열이 주어진 경우, 주어진 배열을 가지고 세그먼트 트리를 구성 
	int init(int start, int end, vector<int> &v) {
		node = make_node();

		if (start == end)  {
			nodes[node].val = v[start];
			return node;
		}
	
		int mid = (start + end) / 2;
		nodes[node].left = init(start, mid, v);
		nodes[node].right = init(mid + 1, end, v);

		nodes[node].val = nodes[nodes[node].left].val + nodes[nodes[node].right].val;
		return node;
	}

	void init(vector<int> &v) {
		init(0, N - 1, v);
	}

	//포인트 업데이트
	int update(int node, int start, int end, int idx, int val) {
		node = copy_node(nodes[node]);//기존 노드를 복사

		if (start == end) {
			nodes[node].val = val;
			return node;
		}

		int mid = (start + end) / 2;

		if (idx <= mid) nodes[node].left = update(nodes[node].left, start, mid, idx, val);
		else nodes[node].right = update(nodes[node].right, mid + 1, end, idx, val);
		
		nodes[node].val = nodes[nodes[node].left].val + nodes[nodes[node].right].val;

		return node;
	}

	void update(int idx, int val) {
		//수정이 발생하는 경우 새롭게 만들어지는 트리의 루트 노드 인덱스를 저장	
		root.emplace_back(update(root.back(), 1, N, idx, val));
	}

	//구간합 쿼리
	int query(int node, int start, int end, int left, int right) {
		if (right < start || end < left) return 0;
		if (left <= start && end <= right) return nodes[node].val; 

		int mid = (start + end) / 2;

		return query(nodes[node].left, start, mid, left, right) + query(nodes[node].right, mid + 1, end, left, right);
	}

	int query(int version, int left, int right) {
		//어떤 버전의 루트 노드를 찾아 쿼리를 수행
		return query(root[version], 1, N, left, right);
	}
};

int update()는 업데이트가 일어날 때마다 해당 업데이트에 영향을 받는 노드들을 copy_node로 복사하고, 그 루트 노드의 nodes에서의 인덱스를 반환한다.

이 인덱스는 root에 저장되어, 후에 찾고자 하는 버전이 있을 때 사용된다.

위 코드를 이용하면 BOJ 16978 수열과 쿼리 22 문제를 풀 수 있다.

5. 예제

BOJ 11012 Egg를 PST를 이용해 풀어보자.

각 점의 $y$ 좌표를 관리하는 세그먼트 트리를 만들고, 점들을 $x$ 좌표 기준 오름차순으로 정렬한 후, $x$ 축 방향으로 스위핑을 진행한다. 스위핑 중 어떤 점을 만나게 되면 그 $y$ 값에 1씩을 더해주자.

어떤 $x$ 까지의 점들에 대한 업데이트를 모두 마친 상태의 자료 구조를 $T_x$ 라 하고, $T_x$ 에서의 구간 $[b, t]$ 에 대한 쿼리를 $T_x(b,t)$ 라고 한다면, 구간 $[l, r] \times [b, t]$ 에 있는 점들의 개수는 $T_r(b,t) - T_{l-1}(b,t)$ 로 셀 수 있게 된다.

//BOJ 11012 Egg

#include <iostream>
#include <vector>
#include <algorithm>
#include <map>
using namespace std;

#define fastio cin.tie(NULL); cout.tie(NULL); ios_base::sync_with_stdio(false)
#define all(v) v.begin(), v.end()

typedef long long ll;

struct Node {
	ll val;
	int left, right;

	Node() : val(0), left(-1), right(-1) {} 

	Node(const Node &node) {
		val = node.val;
		left = node.left;
		right = node.right;
	}
};

struct PST{
	int N;
	vector<Node> nodes;
	map<int, int> root;

	PST(int N, int Q): N(N) { 
		nodes.reserve(4 * N + 18 * Q);
	}

	int copy_node(const Node& node) {
		nodes.emplace_back(node);
		return nodes.size() - 1;
	}

	int make_node() {
		nodes.emplace_back();
		return nodes.size() - 1;
	}

	int init(int start, int end) {
		int node = make_node();

		if (start == end)  return node;
	
		int mid = (start + end) / 2;
		nodes[node].left = init(start, mid);
		nodes[node].right = init(mid + 1, end);

		return node;
	}

	void init() {
		root[0] = init(0, N - 1);
	}	

	int update(int node, int start, int end, int idx) {
		node = copy_node(nodes[node]);

		if (start == end) {
			nodes[node].val++;
			return node;
		}

		int mid = (start + end) / 2;

		if (idx <= mid) nodes[node].left = update(nodes[node].left, start, mid, idx);
		else nodes[node].right = update(nodes[node].right, mid + 1, end, idx);
		
		nodes[node].val = nodes[nodes[node].left].val + nodes[nodes[node].right].val;

		return node;
	}

	void update(int version, int idx) {
		root[version] = update(root.rbegin()->second, 0, N - 1, idx);
	}

	ll query(int node, int start, int end, int left, int right) {
		if (node < 0 || right < start || end < left) return 0;
		if (left <= start && end <= right) return nodes[node].val; 

		int mid = (start + end) / 2;

		return query(nodes[node].left, start, mid, left, right) + query(nodes[node].right, mid + 1, end, left, right);
	}

	ll query(int version, int left, int right) {
		return query(root[version], 0, N - 1, left, right);
	}
};

int main() {
	fastio;

	int T;
	cin >> T;

	while (T--) {
		int N, M;
		cin >> N >> M;

		vector<pair<int, int>> points(N);
		vector<int> xx, yy;

		for (int i = 0; i < N; i++) {
			cin >> points[i].first >> points[i].second;
			xx.emplace_back(points[i].first);
			yy.emplace_back(points[i].second);
		}
		
		sort(all(points));

		auto compress = [](vector<int> &v) {
			sort(all(v));
			v.erase(unique(all(v)), v.end());
		};

		compress(xx); compress(yy);
	
		PST pst(100001, N);
		pst.init();

		for (int i = 0, j = 0; i < N; i = j) {
			while (j < N && points[i].first == points[j].first) j++;

			for (int k = i; k < j; k++) {
				auto &[x, y] = points[k];
				x = lower_bound(all(xx), x) - xx.begin();
				pst.update(x, y);
			}
		}

		ll ans = 0;
		for (int i = 0; i < M; i++) {
			int l, r, b, t;
			cin >> l >> r >> b >> t;

			l = lower_bound(all(xx), l) - xx.begin() - 1;
			r = upper_bound(all(xx), r) - xx.begin() - 1;

			ans += pst.query(r, b, t) - (l >= 0 ? pst.query(l, b, t) : 0);
		}

		cout << ans << '\n';
	}
}

Park Yeongseo

이전 포스트