병합 정렬 (합병 정렬)

• 배열을 앞 부분과 뒷 부분으로 나누어 각각 정렬한 다음 병합하는 작업을 반복하여 정렬을 수행하는 알고리즘
• 1945년 존 폰 노이만(John von Neumann)이 개발
• 안정정렬에 속한다.
• 분할 정복 알고리즘의 하나이다. (퀵 정렬도 분할정복알고리즘)

1. 배열 a에서 선택한 요소(a[pa])와 배열 b에서 선택한 요소 (b[pb))를 비교하여 작은 값을 c[pc]에 저장
2. 커서 pb, pc를 한 칸 옮기고, 커서 pa는 그대로 둠
3. 커서 pa, pb, pc를 진행하는 작업을 반복함
4. 커서 pa가 배열 a의 끝에 다다르거나, 커서 pb가 배열 b의 끝에 다다르면 이 작업을 종료

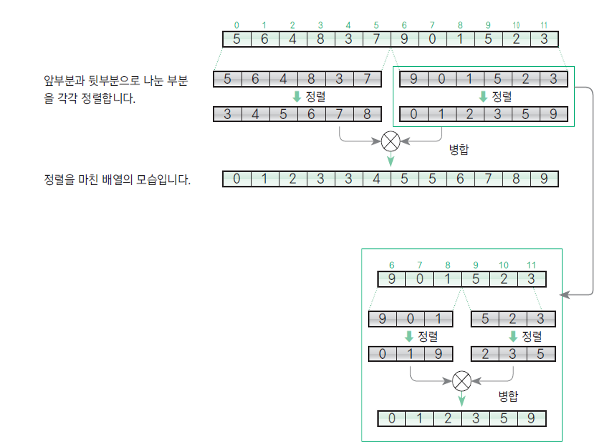
병합 정렬 과정

하나의 리스트를 두 개의 균등한 크기로 분할하고 분할된 부분 리스트를 정렬한 다음, 두 개의 정렬된 부분 리스트를 합하여 전체가 정렬된 리스트가 되게 하는 방법이다.
합병 정렬은 다음의 단계들로 이루어진다.

• 분할(Divide): 입력 배열을 같은 크기의 2개의 부분 배열로 분할한다.
• 정복(Conquer): 부분 배열을 정렬한다. 부분 배열의 크기가 충분히 작지 않으면 순환 호출 을 이용하여 다시 분할 정복 방법을 적용한다.
• 결합(Combine): 정렬된 부분 배열들을 하나의 배열에 합병한다.
  https://gmlwjd9405.github.io/2018/05/08/algorithm-merge-sort.html

/* 병합 정렬 프로그램 */
#include <stdio.h>
#include <stdlib.h>

static int *buff;		/* 작업용 배열 */

/*--- 병합 정렬(main 부분) ---*/
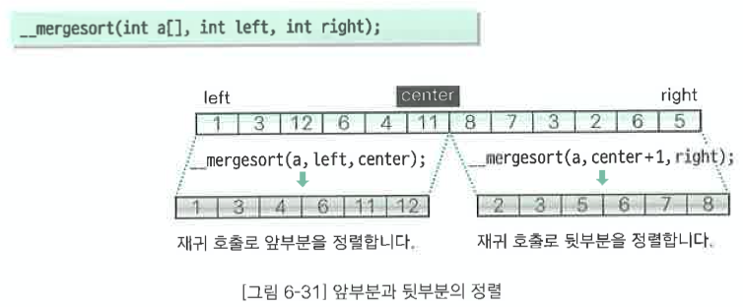
static void __mergesort(int a[], int left, int right)
{
	if (left < right) {
		int center = (left + right) / 2;
		int p = 0;
		int i;
		int j = 0;
		int k = left;

		__mergesort(a, left, center);			/* 앞부분에 대한 병합 정렬 */
		__mergesort(a, center + 1, right);		/* 뒷부분에 대한 병합 정렬 */
		
		for (i = left; i <= center; i++)
			buff[p++] = a[i];

		while (i <= right && j < p)
			a[k++] = (buff[j] <= a[i]) ? buff[j++] : a[i++];

		while (j < p)
			a[k++] = buff[j++];
	}
}

/*--- 병합 정렬 함수 ---*/
int mergesort(int a[], int n)
{
	if ((buff = calloc(n, sizeof(int))) == NULL)
		return -1;
	__mergesort(a, 0, n - 1);		/* 배열 전체를 병합 정렬 */
	
	free(buff);
	
	return 0;
}

int main(void)
{
	int i, nx;
	int *x;				/* 배열의 첫 번째 요소에 대한 포인터 */
	
	puts("병합 정렬");
	printf("요소 개수 : ");
	scanf("%d", &nx);
	x = calloc(nx, sizeof(int));

	for (i = 0; i < nx; i++) {
		printf("x[%d] : ", i);
		scanf("%d", &x[i]);
	}

	mergesort(x, nx);			/* 배열 x를 병합 정렬 */

	puts("오름차순으로 정렬했습니다.");
	for (i = 0; i < nx; i++)
		printf("x[%d] = %d\n", i, x[i]);
	
	free(x);		/* 배열을 해제 */
	
	return 0;
}

배열 병합의 시간 복잡도 : O(n)
병합 정렬의 단계는 log n 만큼 필요
전체 시간 복잡도 : O(n log n)

서로 떨어져 있는 요소를 교환하는 것이 아니므로 안정적인 정렬 방법