1. 재귀
재귀란?
: 어떤 사건이 자기 자신을 포함하고 다시 자기 자신을 사용하여 정의하는 것
1-1. 순차곱셈 구하기 (factorial)
/* 순차곱셈의 결과를 재귀적으로 구합니다. */
#include <stdio.h>
/*--- 정수 n의 순차곱셈 값을 반환 ---*/
int factorial(int n)
{
if (n > 0)
return n * factorial(n - 1);
else
return 1;
}
int main(void)
{
int x;
printf("정수를 입력하세요. : ");
scanf("%d", &x);
printf("%d의 순차곱셈 값은 %d입니다.\n", x, factorial(x));
return 0;
}1-2. 유클리드 호제법으로 최대공약수 구하기
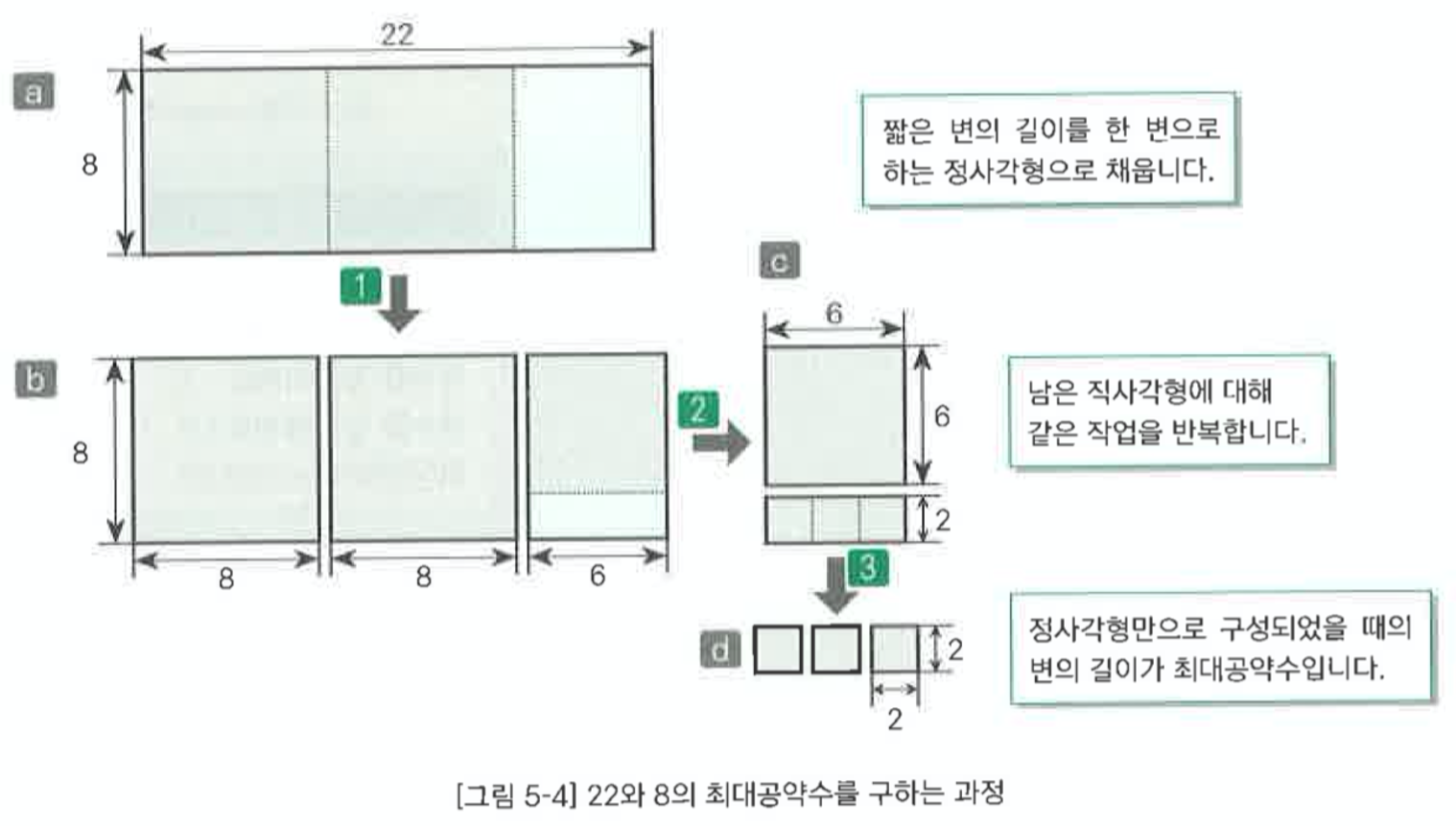
/* 유클리드 호제법에 의해 최대공약수를 구합니다. */
#include <stdio.h>
/*--- 정수 x, y의 최대공약수를 반환 ---*/
int gcd(int x, int y)
{
if (y == 0)
return x;
else
return gcd(y, x % y);
}
int main(void)
{
int x, y;
puts("두 정수의 최대공약수를 구합니다.");
printf("정수를 입력하세요 : ");
scanf("%d", &x);
printf("정수를 입력하세요 : ");
scanf("%d", &y);
printf("최대공약수는 %d입니다.\n", gcd(x, y));
return 0;
}2. 재귀 알고리즘 분석
하향식 분석 (Top-down analysis)
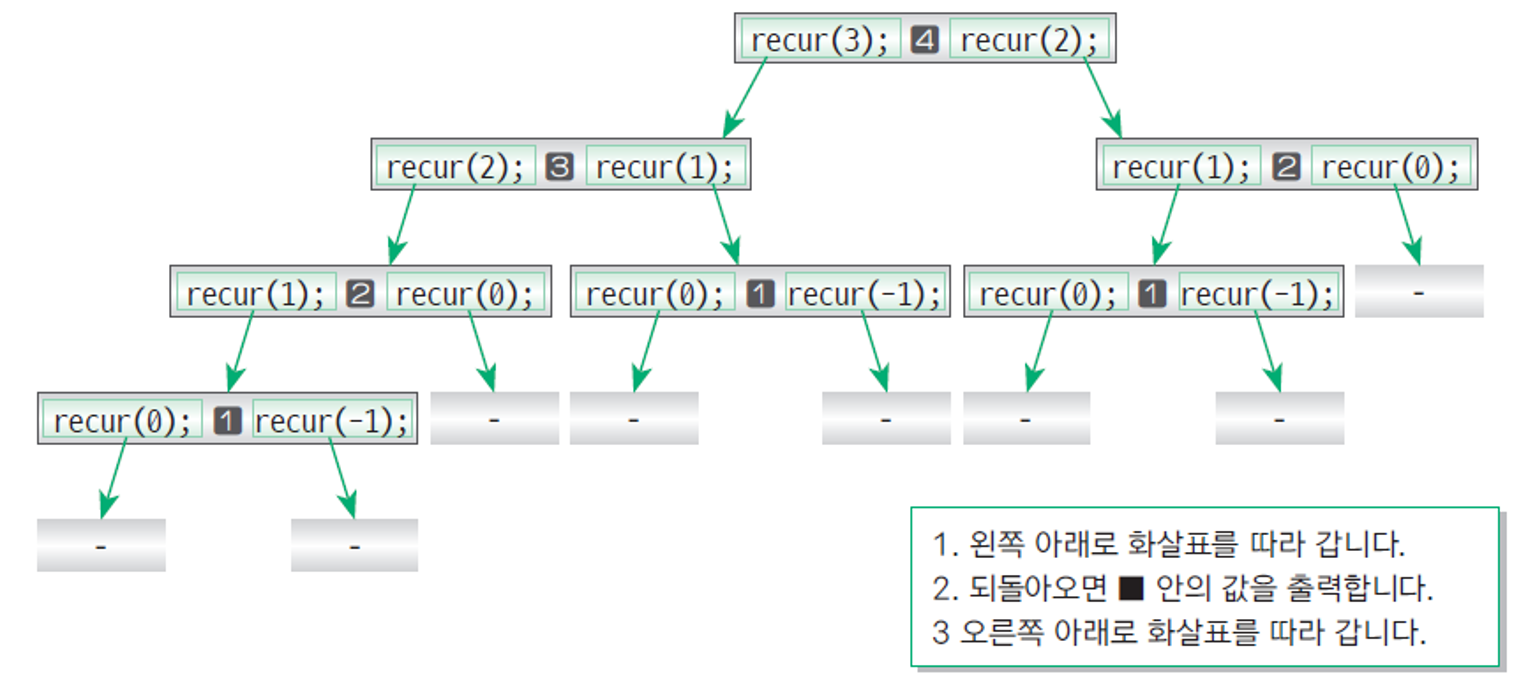
이처럼 가장 위쪽에 위치한 함수 호출부터 시작해 계단식으로 자세히 조사해 가는 분석 기법을 하향식 분석(top-down analysis)이라고 합니다.
상향식 분석 (Bottom-up analysis)
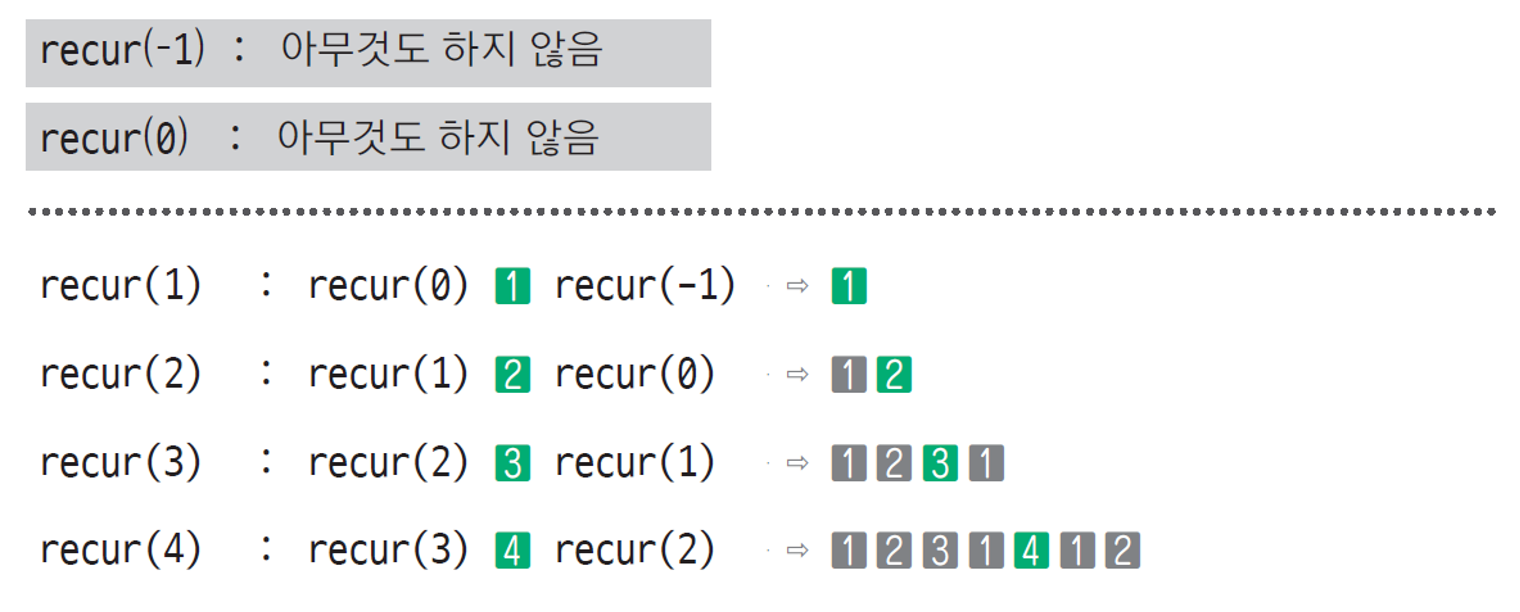
하향식 분석과는 반대로 아래쪽부터 쌓아 올리며 분석하는 방법이 상향식 분석(bottom-up analysis)입니다.
재귀 알고리즘의 비 재귀적 표현
일반 재귀와의 큰 차이점 : 반환값에서 추가연산을 필요로 하지 않는다.
2-1. 일반 재귀 팩토리얼
int factorial(int num){
if(num == 0) return 1;
int callResult = factorial(num - 1);
return num * callResult; // 재귀 호출 이후 추가적인 연산이 필요하다.
}2-2. 꼬리 재귀 팩토리얼 (꼬리 재귀의 제거)
int factorialTail(int n, int acc){
if(n == 1) return acc;
return factorialTail(n - 1, acc * n);
}
int factorial(int n){
return factorialTail(n, 1);
}팩토리얼 함수가 두개로 분리되었는데, 요점은 재귀 호출 이후 추가적인 연산을 요구하지 않도록 구현하는 것이다.
일반 재귀로 구현된 factorial 함수는 재귀 호출을 하고 나서, num 을 곱하는 연산이 존재한다.
따라서 일반 재귀로 구현된 함수는 아래 함수와 같이 동작한다.
2-3. goto문으로 해결한 꼬리재귀알고리즘
/* 재귀에 대한 이해를 깊게하는 진짜 재귀 함수 */
#include <stdio.h>
/*--- 함수 recur (맨끝 재귀를 삭제) ---*/
void recur(int n)
{
Top:
if (n > 0) {
recur(n - 1);
printf("%d\n", n);
n = n - 2;
goto Top;
}
}
int main(void)
{
int x;
printf("정수를 입력하세요. :");
scanf("%d", &x);
recur(x);
return 0;
}2-4. stack문으로 해결한 재귀의 제거
recur(n-1);
printf("%d", n);
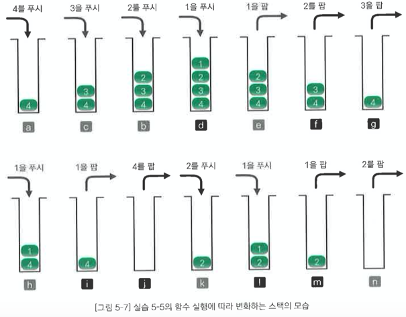
recur(n-2);예를 들어, n = n - 1로 구현하면 n은 3이 되기 때문에, 재귀 호출 recur(3)의 처리가 완료되지 않으면 n의 값인 '4'를 저장해야 합니다. 따라서 변수 n의 값을 잠시 저장해야 합니다. 이런 데이터 구조가 stack입니다. 다음은 스택을 이용하여 비재귀적으로 구현한 recur 함수입니다.
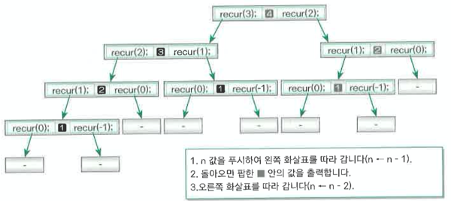
1. n값을 푸시하여 왼쪽 화살표를 따라갑니다(n = n - 1)
2. 돌아오면 pop한 스택의 값을 출력합니다.
3. 오른쪽 화살표를 따라 값니다(n = n - 2)
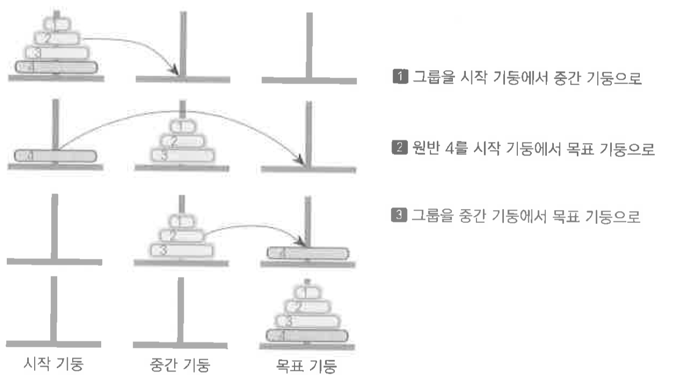
3. 하노이의 탑
/* 하노이의 탑 */
#include <stdio.h>
/*--- 원반[1] ~ 원반[no]를 x 기둥에서 y 기둥으로 옮김 ---*/
void move(int no, int x, int y)
{
if (no > 1)
move(no - 1, x, 6 - x - y); /* 그룹을 시작 기둥에서 중간 기둥으로 */
printf("원반[%d]를 %d 기둥에서 %d 기둥으로 옮김\n", no, x, y); /* 바닥 원반을 목표 기둥으로 */
if (no > 1)
move(no - 1, 6 - x - y, y); /* 그룹을 중간 기둥에서 목표 기둥으로 */
}
int main(void)
{
int n; /* 원반의 개수 */
printf("하노이의 탑\n원반 개수 : ");
scanf("%d", &n);
move(n, 1, 3);
return 0;
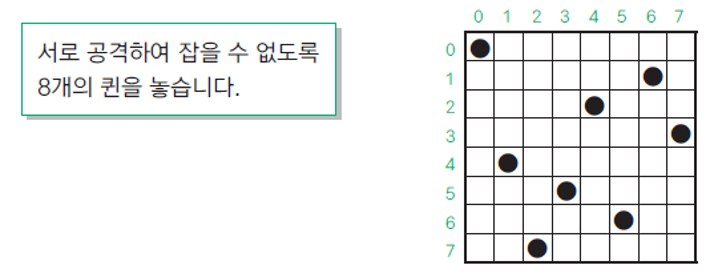
}4. 8퀸 문제
참고 )
- (내 손으로 직접 코딩하며 확인한다!) 자료구조와 함께 배우는 알고리즘 입문 - C 언어 편
- 꼬리 재귀
https://velog.io/@dldhk97/재귀함수와-꼬리-재귀- 재귀의 제거
https://velog.io/@jimmy48/재귀-알고리즘-분석

