영상 처리 6주차 - 빛 밝기 개선 문제점 해결
시작하기에 앞서
지난 5주차때까지 밝기 개선 작업을 수행해보았다.
"Histogram Equalization", "Histogram Stretching"을 주 연산으로써 영상 이미지의 밝기 개선을 진행해보았으나 어두운 이미지를 밝게 하는 것엔 만족스럽게 적용이 되었지만 빛 번짐이나 극도로 밝은 조명에선 제대로 수행이 되지 않았다.
그에 따라 "CLAHE(Contrast Limited Adaptive Histogram Equalization)" 연산을 수행해 보았지만 하지만 이 역시 빛 번짐과 밝은 조명에서는 크게 개선을 시키지 못하였다.
사실 극도로 밝은 영역은 쉽게 개선될 수 없다. 하지만 이번 프로젝트를 진행하면서 이 부분에 시간을 많이 투자했고 조금 더 나은 방법을 찾아본 결과를 이번 포스팅에서 작성해보고자 한다.
시도한 방법
방법 1 -- 해당 영역 픽셀 강제 변환
여태껏 히스토그램 조작을 통해 이미지 밝기 개선을 한 것은 이미지 전체의 영역에 대해 개선을 한 것이다. 그에 따라서 이미지의 특정 영역(빛 번짐 영역)을 개선하는 것에 어려움이 있으므로 아주 간단한 접근으로써 이 문제를 해결해보고자 한다.
이미지의 빛 번짐이 있는 영역은 BGR 색상으로써 [255, 255, 255] 값을 가질 것이다. 이미지 전체의 width와 height 값을 돌면서 해당 픽셀값이 있는 곳의 색상을 강제적 다른 색상으로 변화하는 것을 시도해 보았다.
for y in range(0, imgHeight):
for x in range(0, imgWidth):
B_pixel = y, x, 0
G_pixel = y, x, 1
R_pixel = y, x, 2
B = dst.item(y, x, 0)
G = dst.item(y, x, 1)
R = dst.item(y, x, 2)
BGR = [B, G, R]
if (BGR == [255, 255, 255]):
dst.itemset(B_pixel, 225)
dst.itemset(G_pixel, 225)
dst.itemset(R_pixel, 250)우리가 히스토그램 평활화 작업을 할때도 RGB 요소로 한번에 묶어서 작업을 수행하는 것이 아닌 R G B 각각의 요소를 split을 통하여 분리시키고 평활화 과정을 수행 후 merge시켜주었다. 위의 방법도 동일한 접근이다.
itemset이란 메서드를 사용하여 각 R, G, B의 값을 임의로 조정해 줄 수 있다.
InputImg

dst_Img

Histogram Analysis
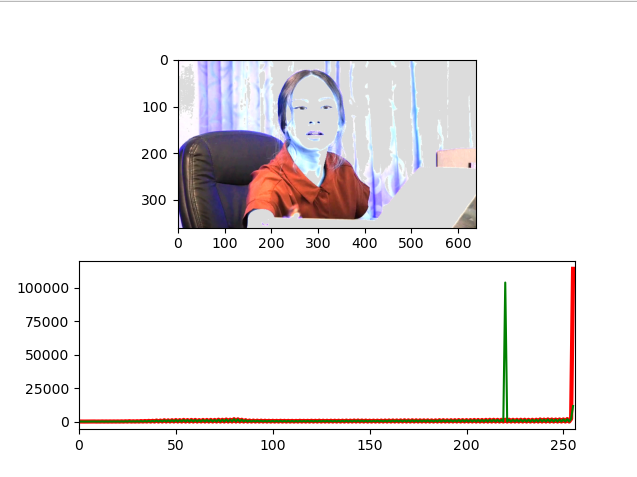
이것은 사실 본인이 한 접근중에 하나이지 해결법이라곤 할 순 없었다. 이미지의 빛 번짐 영역 ( [255, 255, 255]에 쏠려있던 영역 )을 떨어뜨릴 순 있었지만 얼굴 인식과 물체 인식의 측면에서는 좋지 않은 접근이다.
Homomorphic Filter (준동형 필터링)
다시 언급하지만 지금 해결하고자 하는 이슈는 이미지에 따라 빛(자연, 조명)이 노출되는 방향이나 세기 정도가 제각기 다르기 때문에 해당 빛을 normalize하는 과정이 필요한 것이다. 앞서 첫번째 제시한 방법은 색 자체를 변경시키는 것이므로 normalize와는 거리가 멀다. 조금 더 쉽게 말하자면 빛 번짐 영역의 색상 자체를 떨어뜨리기 보단 색을 조금 더 연하게, 농도를 연하게 하는 과정이 필요한 것이다.
그러던 와중 발견한 방법이 Homomorphic Filter이다.
"Homomorphic filtering is sometimes used for image enhancement. It simultaneously normalizes the brightness across an image and increases contrast."
영상의 픽셀 강도는 크게 2가지 영향을 받는다. 하나는 조명과 같은 직접적인 광원으로부터의 빛 "illumination element(i(x, y))", 나머지 하나는 객체로부터 반사된 빛 "reflectance element(r(x, y))"이다.
"Illumination and reflectance are not separable, but their approximate locations in the frequency domain may be located."
조명과 반사율은 분리 할 수 없지만 주파수 영역에서 대략적인 위치를 찾을 수 있다.
조금 더 자세히 말하면 "illumination element"는 이미지에 노출된 조명을 나타내고 이것은 low frequency로 표현할 수 있다. 그리고 "reflectance element"는 이미지에 존재하는 오브젝트들의 edge를 나태내고 high frequency로 표현할 수 있다.
이렇게 디지털 영상은
f(x, y) = i(x, y)*r(x, y)로 표현될 수 있다.
하지만 아쉽게도 이 식은 유효하지 않다. 조금은 어려울 수 있는 얘기지만 해당 "Homomorphic Filtering"은 "Frequency(주파수)영역"에서 필터를 적용시키는 것이다. 즉, 우리는 주파수 영역에서 시스템을 분석해야한다는 것이고 해당 방법으로는 푸리에 변환 혹은 라플라스 변환 과정을 수행해야한다.
결국 적분을 해야하게 되는데 그렇게 된다면 아래와 같이 표현된다.
F{f(x, y)} = F{i(x, y)}*F{r(x, y)}하지만 위식은 "=" 관계가 성립되지 않는다. 적분을 취했기 때문이다.
"We have to transform the equation into frequency domain in order to apply high pass filter. However, it's very difficult to do calculation after applying Fourier transformation to this equation because it's not a product equation anymore. Therefore, we use 'log' to help solving this problem."
고역 통과 필터를 적용하기 위해서는 방정식을 주파수 영역으로 변환해야 한다.
그러나 이 방정식은 더 이상 곱의 방정식이 아니기 때문에 푸리에 변환을 적용한 후에는 계산하기가 매우 어렵다. 그러므로 우리는 "log"를 이용하여 이를 해결한다.
덧셈 연산으로 만들어주기
ln f(x,y) = ln i(x,y) + ln r(x,y)
F{ln f(x,y)} = F{ln i(x,y)} + F{ln r(x,y)}이렇게 로그를 취해준 뒤 적분을 하게 되고 필터링의 과정을 거친 후 추후 제대로 된 출력 영상을 얻기 위해서 자연상수 e를 이용해 지수를 취함으로써 얻는 과정으로 진행하는 것이다.
조금 풀어서 설명하자면 log를 취해 덧셈으로 만들어 준 연산에

HPF (high pass filter)를 씌운 뒤 다시 exp연산을 통해 log를 지워줌으로써 최종 조명이 제거된 (개선된) 이미지를 얻게 되는 것이다.
이때 HPF 하는 과정을 주목해 볼 필요가 있다.
우리가 영상의 조명 성분과 반사 성분을 제어하기 위해서 주파수 도메인에서 작업을 하였다. 하지만 결국 우리가 얻어야 할 필터링된 결과는 영상 도메인 이어야한다.
수식으로써 알아보자면
먼저 필터링을 한 뒤
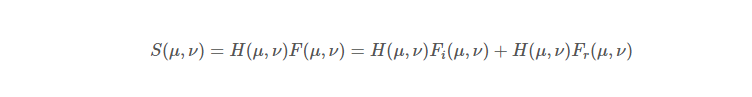
필터링 된 값을 다시 역푸리에 변환을 통해서 영상 도메인으로 바꾸는 것이다.
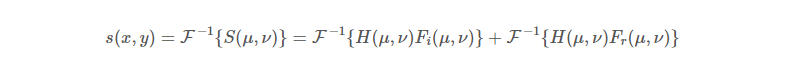
그 후 해당 수식에 자연상수 e를 취함으로써 최종 출력영상을 얻을 수 있다.
이러한 일련의 과정을 "Homomorphic Filtering(준동형 필터링)" 이라 하고 필터 함수 "H(µ, v)"를 "준동형 필터 함수" 라고 한다.
영상 내에서 i(x, y)는 "빛"을 의미함으로 공간에 따라 천천히 변하고 "반사"를 의미하는 r(x, y)는 상이한 객체가 접하는 지점에서 급격하게 변한다.
즉, i(x, y)는 저주파와 관련이 있고, r(x, y)는 고주파와 관련이 있다 볼 수 있다.
우리는 코드에서 이러한 개념을 도입해, 저주파 성분과 고주파 성분에 서로 다른 제어를 할 수 있고 그에 따라서 이루고자하는 빛 번짐에 대한 개선을 이룰 수 있다고 본다.
코드 알아보기
dst = var_img.copy()
dst_YUV = cv2.cvtColor(dst, cv2.COLOR_BGR2YUV)
y = dst_YUV[:, :, 0]
rows = y.shape[0]
cols = y.shape[1]
imgLog = np.log1p(np.array(y, dtype='float') / 255)
M = 2*rows + 1
N = 2*cols + 1
sigma = 10
(X, Y) = np.meshgrid(np.linspace(0, N-1, N), np.linspace(0, M-1, M))
Xc = np.ceil(N/2)
Yc = np.ceil(M/2)
gaussianNumerator = (X - Xc)**2 + (Y - Yc)**2
LPF = np.exp(-gaussianNumerator / (2*sigma*sigma))
HPF = 1 - LPF
LPF_shift = np.fft.fftshift(LPF.copy())
HPF_shift = np.fft.fftshift(HPF.copy())
img_FFT = np.fft.fft2(imgLog.copy(), (M, N))
img_LF = np.real(np.fft.fft2(img_FFT.copy() * LPF_shift, (M, N)))
img_HF = np.real(np.fft.fft2(img_FFT.copy() * HPF_shift, (M, N)))
gamma1 = 1.2
gamma2 = 1.5
img_adjusting = gamma1*img_LF[0:rows,
0:cols] + gamma2*img_HF[0:rows, 0:cols]
img_iLF = (np.fft.ifft2(img_FFT.copy() * LPF_shift, (M, N)))
img_iHF = (np.fft.ifft2(img_FFT.copy() * HPF_shift, (M, N)))
img_adjusting = gamma1*img_iLF[0:rows, 0:cols] + gamma2*img_iHF[0:rows, 0:cols]
img_exp = np.expm1(img_adjusting) # exp(x) + 1
img_exp = (img_exp - np.min(img_exp))
(np.max(img_exp) - np.min(img_exp)) # 0~1사이로 정규화
img_out = np.array(255*img_exp, dtype='uint8') # 255를 곱해서 intensity값을 만들어줌
dst_YUV[:, :, 0] = img_out
dst = cv2.cvtColor(dst_YUV, cv2.COLOR_YUV2BGR)결과 알아보기
InputImg

dst_Img (필터링한 개선 이미지)

Hist Analysis
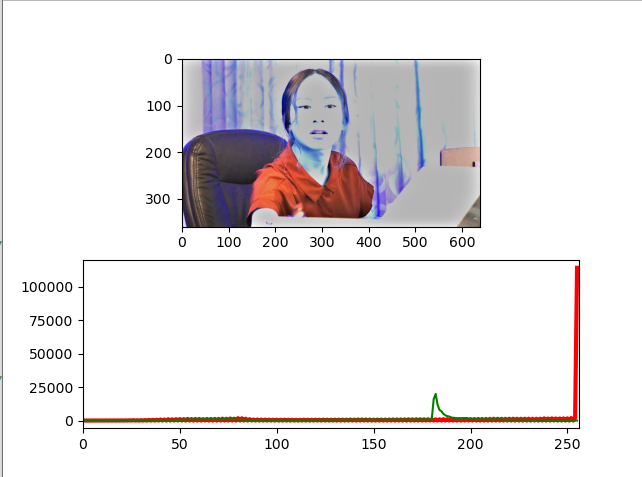
생각정리
생각정리는 Homomorphic Filtering 코드에 대한 이해가 완료 후 추후 작성...
