마이크로 명령과 ALU
마이크로 연산
레지스터에 저장된 데이터에 대해 수행되는 기본적인 연산
마이크로 연산의 분류
- 레지스터 사이에서 이진 정보를 전송하는 레지스터 전송 마이크로 연산
- 레지스터에 저장된 수치 데이터에 대해 산술 연산을 수행하는 산술 마이크로 연산
(ALU, 버퍼) - 레지스터에 저장된 비수치 데이터에 대해 비트 조작 연산을 수행하는 논리 마이크로 연산 (OR, AND, NOT, XOR)
- 레지스터에 저장된 데이터에 대해 시프트 연산을 수행하는 시프트 마이크로 연산
ex) 0010 << 2 = 1000, 0100 >> 1 = 0010
산술 논리 연산 장치 (ALU)
산술 연산과 논리 연산을 처리한다.
- 주로 정수 연산을 처리
- 부동 소수 연산 처리
산술 연산 - 덧셈, 뺄셈, 곱셈, 나눗셈, 증가, 감소, 보수
논리 연산 - AND, OR, NOT, XOR, shift
ALU의 역할
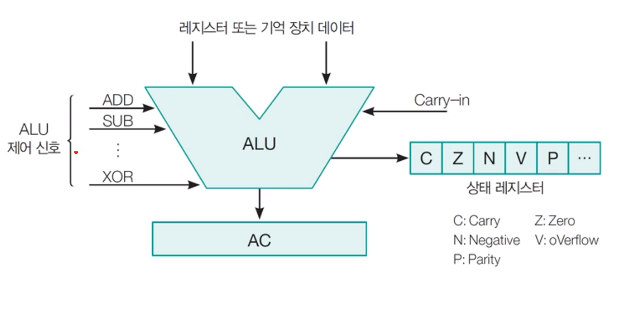
- 산술, 논리 연산 명령어가 들어왔을 때 레지스터에서 참조할 값을 가져와서 연산 수행 (이전에 캐리 비트가 있다면 같이 연산)
- 연산 중 발생한 캐리 비트, 오류 발생 같은 상태를 상태 레지스터에 저장
- 연산된 값을 AC에 누적
- Parity - 오류가 발생했는지 체크
- Negative - 부호가 바뀜
- AC(Accumulator) - 데이터를 일시적으로 보관하는 누산기
산술 연산의 종류
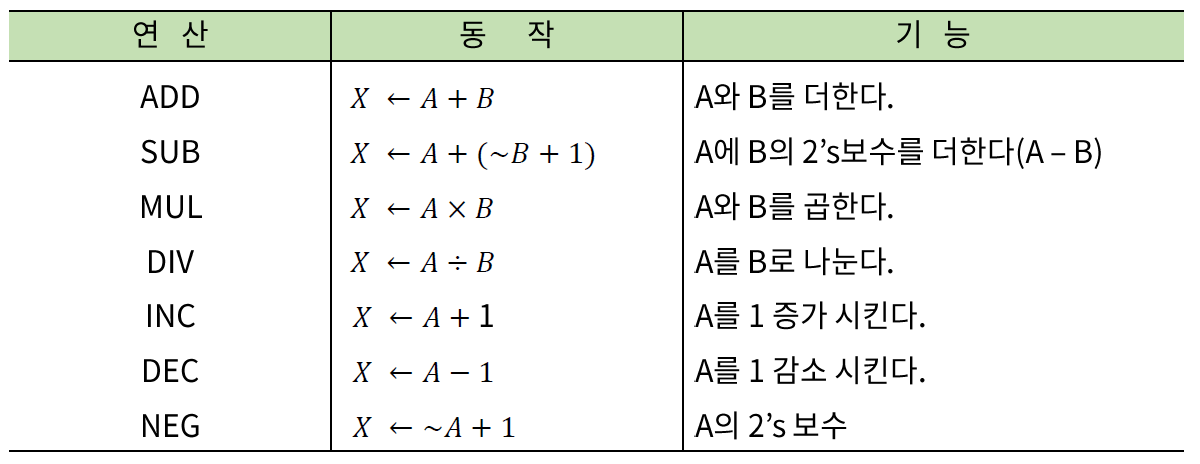
- ~B - B에 대한 1의 보수
논리 연산과 시프트 연산의 종류
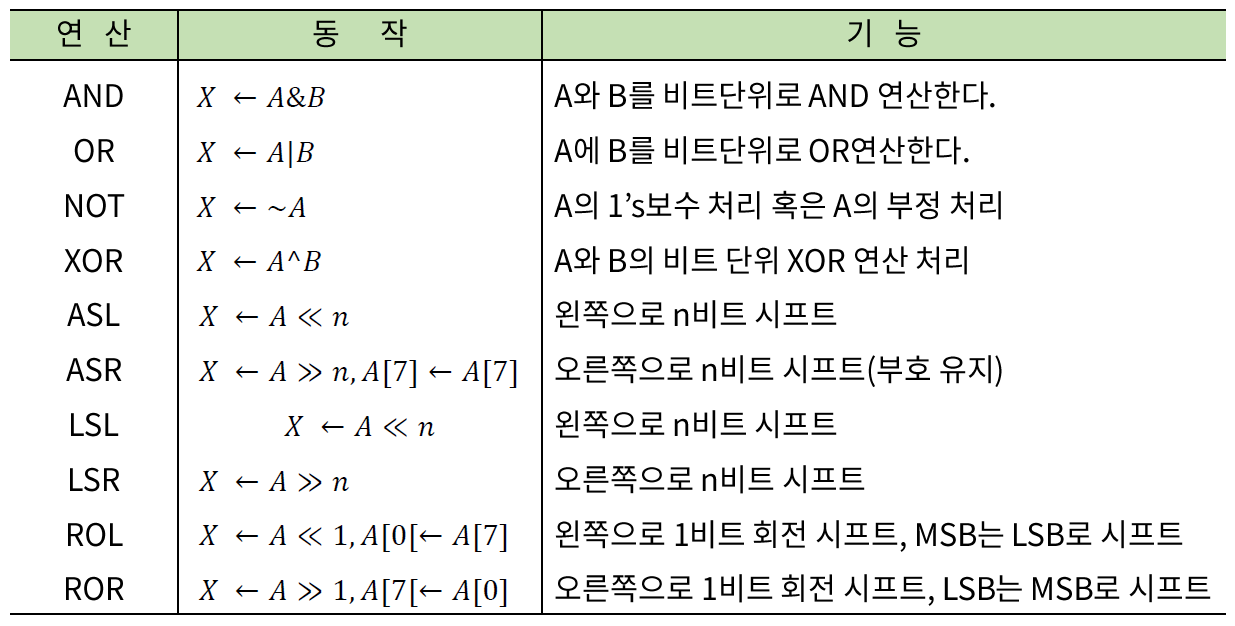
- ALU가 처리하는 논리 연산과 산술 시프트 연산은 다 비트 단위로 연산을 한다.
- MSG - 최선미에 있는 비트
- LSG - 최후미에 있는 비트
논리 연산 예
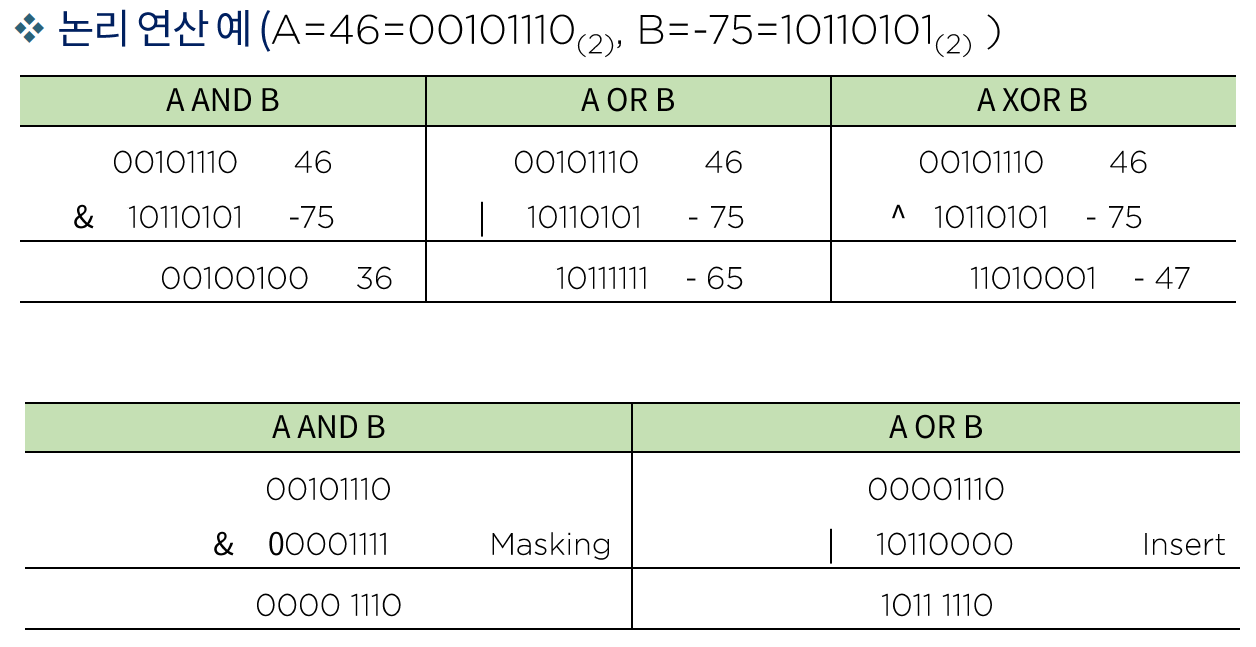
-
Masking - 하위 비트만 남기는 연산
-
Insert - B의 PCH(상위 비트)와 A의 PCL(하위 비트)를 합치는 연산
packed decimal <-> unpacked decimal
변환 과정에서 사용된다.
시프트 연산 예
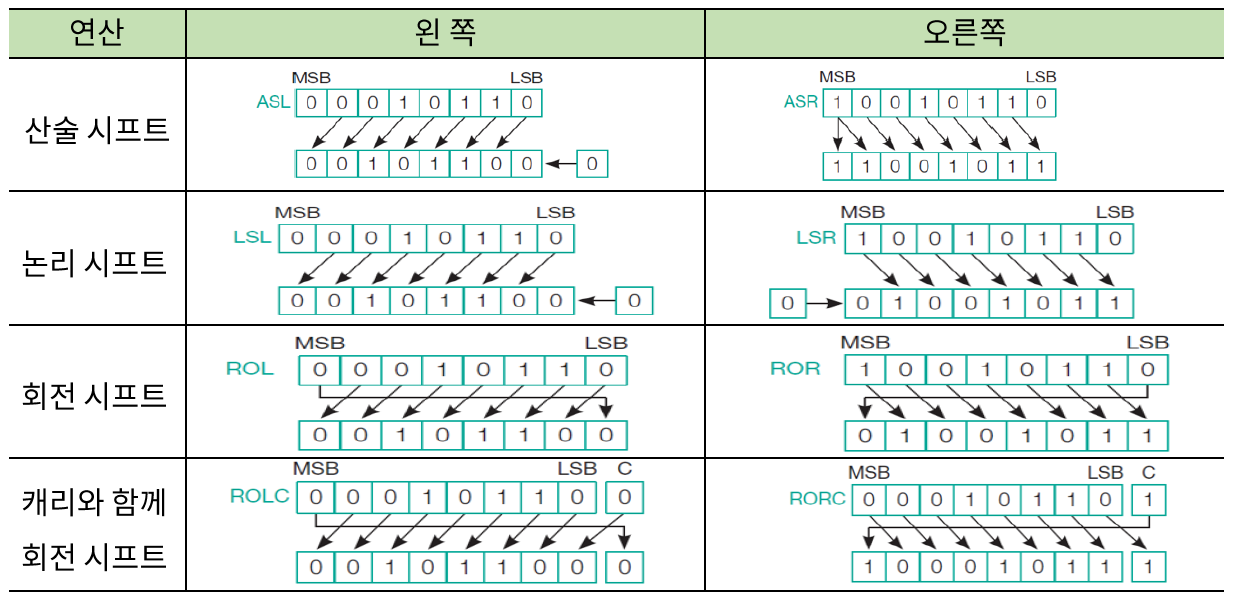
다 성능 좋은 ALU를 만들기 위해 고안된 연산들이다.
마이크로 명령어 집합과 구성
step by step에 의한 처리는 한계가 왔다. -> 병렬 처리 머신(양자 컴퓨터)가 필요하다.
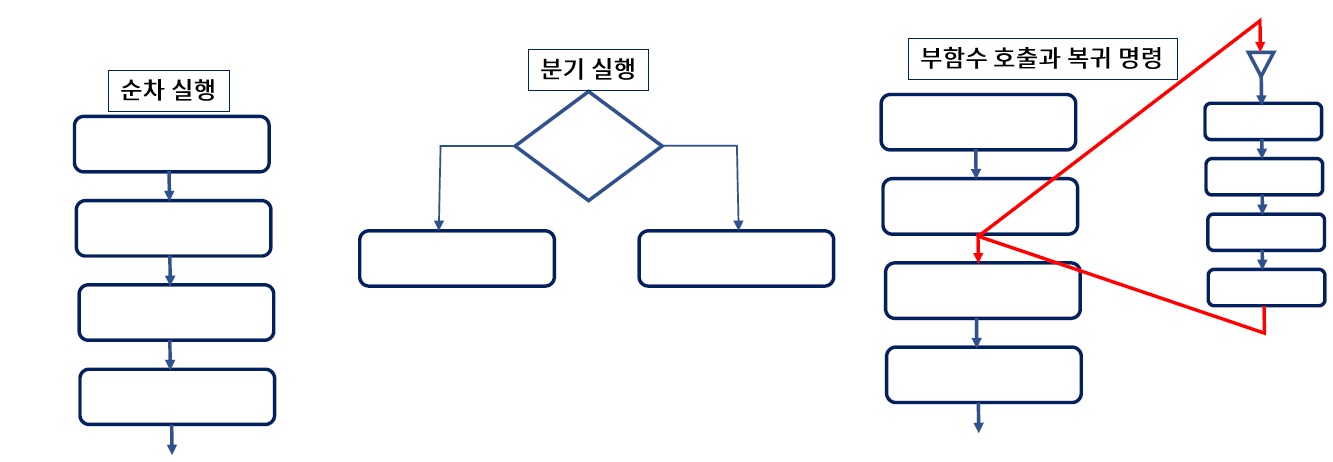
실행 순서에 따른 명령어 분류
- 순차적 실행 명령어 - 전체 실행 명령어의 70~80% 차지 / 가장 익숙한 타입
- 분기 명령어
ex)P: R1 <- R2 = if (P == 1) then R1 <- R2 - 부 함수 호출 명령어
- 복귀 명령어
메인과 서브로 나누어져있고 메인이 실행되는 중간에 서브가 실행된 후 서브의 실행이 끝나면 메인으로 피드백된다.
명령어 구문 형식
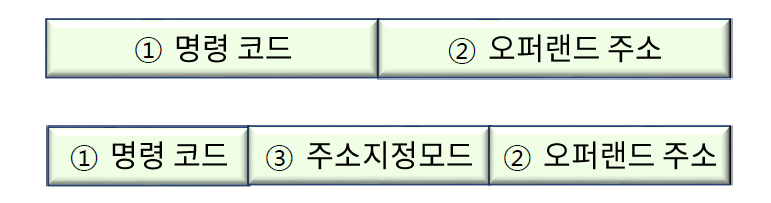
- 위는 direct mode, 아래는 indirect mode
명령어 코드가 복잡해지는 이유는 프로그램과 하드웨어 간의 독립성을 위해서이다.
그래서 direct mode에서 indirect mode로 변화하였다.
소프트웨어가 오퍼랜드 주소를 바꿔도
하드웨어가 자체적으로 찾아서 연산할 수 있게끔 설계됐다.
- 명령 코드 - CPU가 실행할 수 있도록 디자인 된 연산 (ADD, SUB, LOAD...)
- 오퍼랜드 - 연산에 사용되는 자료 값, 자료가 저장된 주소에 관한 정보
- 주소 지정 모드(Addressing mode) - 오퍼랜드가 저장된 위치를 인덱싱 하는 방법 (C언어의 pointer)
명령어 집합의 설계
개인적인 생각으로 자연어에 가까운 코드는 Python, 기계 중심의 코드는 C 같다.
현업에서 활용되는 명령어군의 활용 비율
위의 명령어가 전체 실행 명령어의 90% 이상을 차지한다.
명령어의 쓰임새를 알고 분석하면 더 좋은 명령어를 만들어낼 수 있고 고로 더 좋은 CPU와 ALU가 만들어진다.
주소 지정 모드 (Addressing mode)
명령어의 구조상 자료가 저장되어있는 장소를 지정하는 방법이 필요한데,
이유는 하드웨어와 소프트 웨어의 독립성을 유지하여 프로그램의 유연성(pointer, indexing)을 가능하게 하여 명령어의 수와 길이를 줄이기 위함이다. (세계적 표준화 기법이다.)
묵시적 모드 (operand가 명령에 포함되어 있지 않은 특수 모드)
- NOP: NO operation, 오퍼랜드가 필요 없는 명령어 ex)
MOV R1, R2(이동 명령) - INC: INCREASE 묵시적 오퍼랜드인 누산기(AC)의 연산 명령어 (증가 명령)
- ADD: 스택 구조의 명령어 (스택에 오퍼랜드가 저장)
직접 값 모드 (operand 자체가 명령어에 포함되어 있는 모드)
ex) MOV R1, #100; 십진수 값 100이 두 번째 오퍼랜드로 직접 명령문에 포함
레지스터 모드 (Register mode: operand가 레지스터에 저장된 모드)
ex) ADD R1, R2; 레지스터 R1과 R2에 보유하고 있는 값이 오퍼랜드
메모리 직접 주소 모드 (Direct mode: operand가 저장된 메모리 주소를 나타내는 모드)
ex) MOV R1, 100; R1에 100번지의 내용을 이동하라는 내용, 100번지의 내용이 오퍼랜드
메모리 간접 주소 모드 (Memory indirect addressing mode: 메모리를 이용하여 간접적으로 주소를 지정하는 모드)
ex) MOV R1, @100; R1 <- M[100]
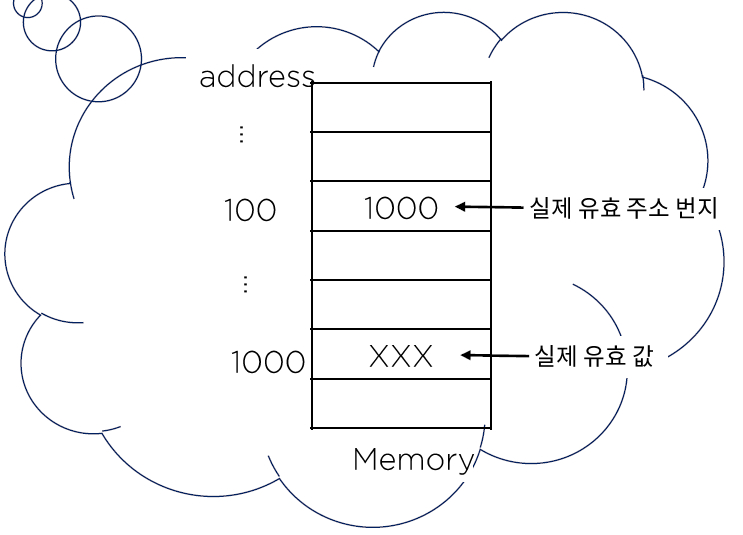
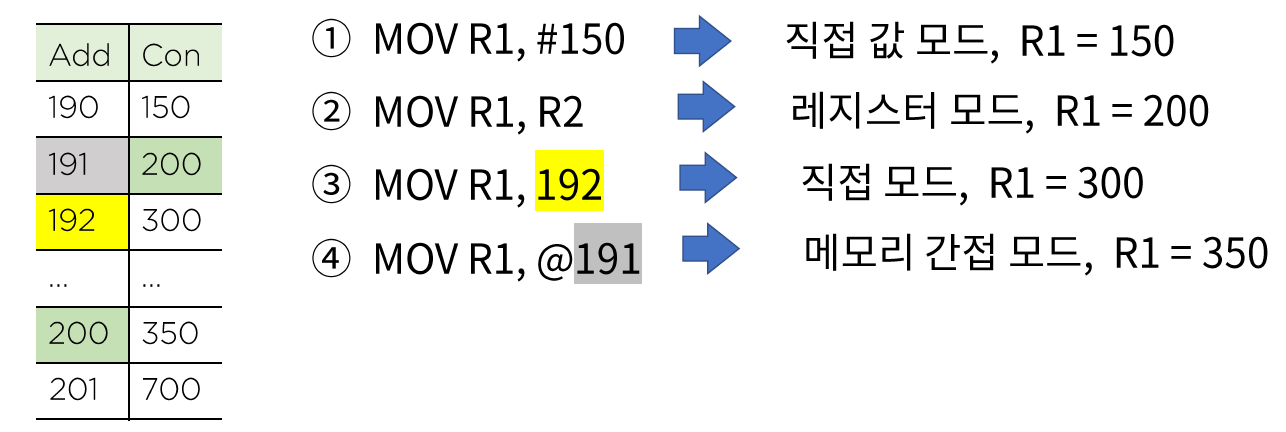
주소 지정 모드 예
다음 마이크로 명령을 수행한 후, 어떤 변화가 생겼을까?
(R1 = 100, R2 = 200이라고 가정)
마이크로 명령 - 입출력과 인터럽트
컴퓨터는 사용자와 통신을 하기 위해서 외부 장치, 즉 메모리로 데이터와 명령어를 읽어들일
입력 장치(input-device)와 계산 결과를 사용자에게 표시해줄 출력 장치(output-device)를 갖추어야 한다.
입출력 구성
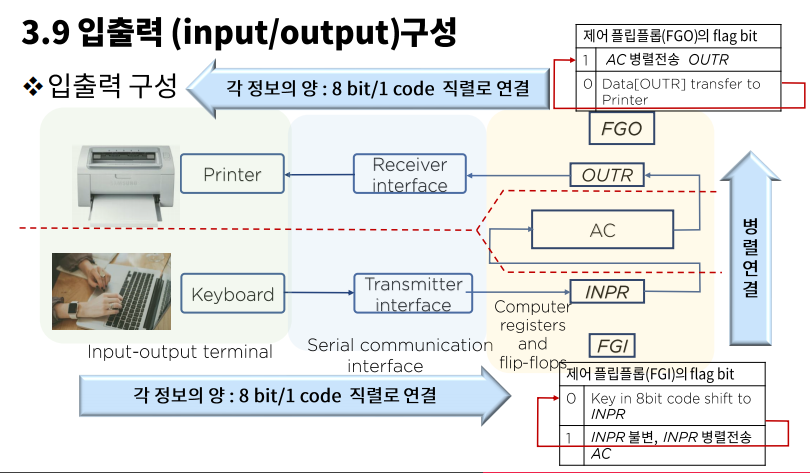
- terminal 하드웨어 장치
- interface 전송 체계
- AC 핵심 코어
FGI/FGO : INPR이나 OUTR에 정보가 override 되는 것을 막기 위해 플래그를 준다. (0일 때는 값이 들어갈 수 있는 것, 1일 때는 값이 들어가지 않음)
- 사용자 키보드 입력
- 직렬로 INPR에 쌓임
- 다 쌓이면 FGI가 1로 바뀌고 AC에 병렬로 전송 후, 다시 0으로 바뀜. 이 때 INPR에 있는 값은 불변(키보드 입력해도 안 바뀜)
- AC는 OUTR에 병렬로 전송
- 다 쌓이면 FGO가 1로 바뀌고 직렬로 printer로 전송 후, 다시 FGO가 0으로 바뀐다.
인터럽트 인에이블 플리플롭 (Interrupt enable flip-flop, IEN )
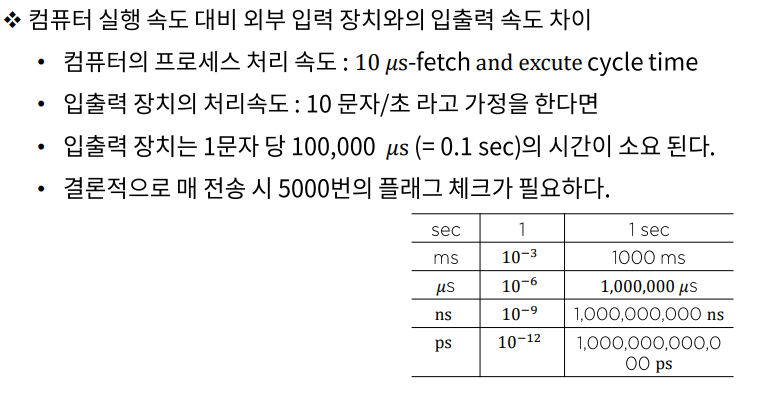
플래그를 이용한 통신 방법을 프로그램 제어 전송(program controlled transfer)이라고 하는데 이것은 프로세스와 입출력 장치와의 속도 차이 때문에 메우 비효율적이다. (컴퓨터 프로세스의 속도가 훨씬 빠름)
이러한 상황을 해결하고자 고안된 인터럽트를 걸 수 있는 플리플롭이다.
플래그를 세트하면 CPU는 실행중이던 프로그램을 중지하고 우선으로 진행될 정보를 플래그의 세트 정보로부터 받아들여 실행 후에 다시 원 프로그램으로 복귀한다.
인터럽트 사이클 흐름도
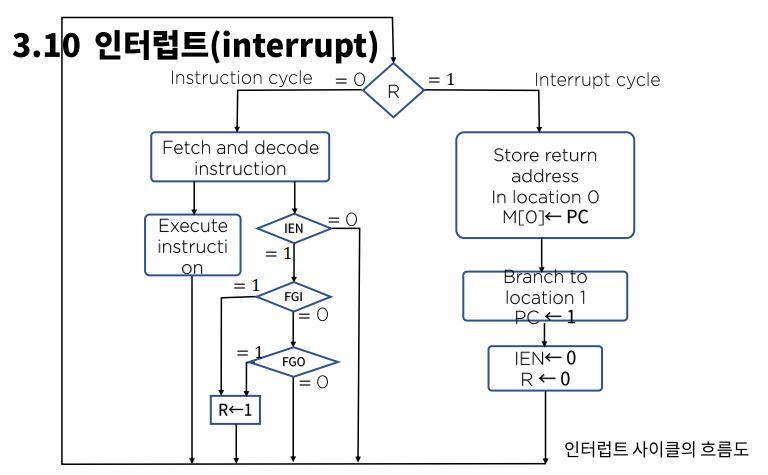
인터럽트 사이클 흐름도 설명
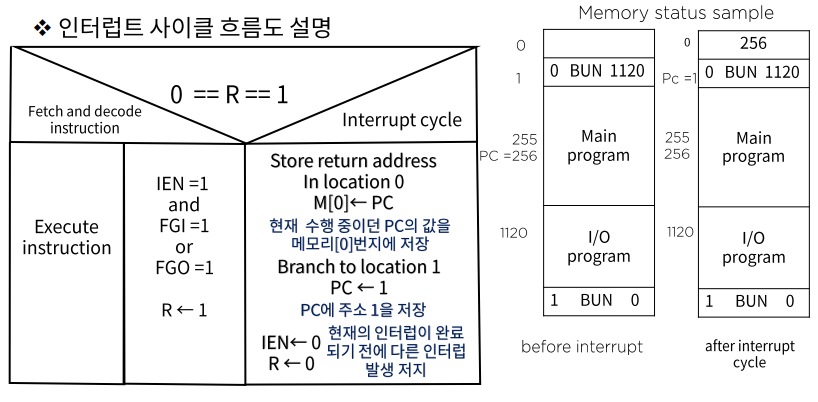
- 메모리 주소 255에 있는 명령이 실행되던 중,
R = 1이 되어 인터럽트 발생 M[0] <- 256,PC <- 1저장 /IEN = 0,R = 0저장- Excute M[1]: 1120 주소로 번지하여 I/O program 실행
- PC는 다음 명령어를 가리키고 M[1121]을 실행하면
PC <- 0실행 PC <- 256실행이 돼서 원래 수행중이던 명령으로 복귀
기본 컴퓨터 프로그래밍
- 하드웨어 - 신체
- 소프트 웨어 - 정신
하드웨어를 잘 동작시킬 수 있게 제어 및 지시하는 모든 종류의 프로그램
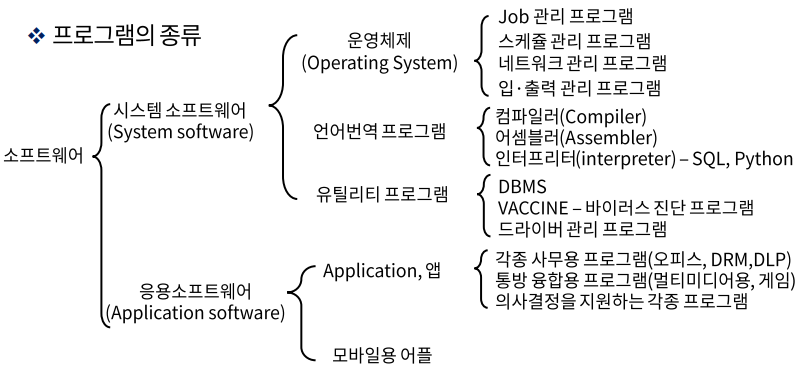
- 시스템 소프트웨어 - 하드웨어를 관리
- 응용 소프트웨어 - 개발자가 만드는 Application
프로그램 처리 과정

처음엔 기계어로 프로그램을 만들다가
프로그램이 커지면서 유지보수가 힘들어지자 어셈블리어를 만들었는데
어셈블리어는 컴퓨터의 내부 동작(IEN)을 다 신경 써서 해야하고 표준화 되어있지 않아서
고급 언어가 등장했다.
-
컴파일러: 고급 언어 -> 어셈블리어 -> 기계어 단계로 번역
컴파일 되면 오브젝트 코드 파일로 변환되고 필요 시 실행할 수 있다. -
인터프리터: 고급 언어 -> 어셈블리어 -> 기계어 단계로 번역
해석과 동시에 실행한다. -
어셈블러: 어셈블리어 -> 기계어 단계로 번역
기계어
프로그램이란 컴퓨터로 하여금 원하는 데이터처리 업무를 시행시키기 위해서 작성된 명령어 또는 문장으로 구성된 리스트이며 다음과 같은 종류가 있다.
-
이진 코드 - 메모리 상에 나타나는 형태의 명령어로서 이진 명령어와 피연산자의 시퀀스다.
어셈블리어로 예를 들면) ADD 101, 102 -
8/16진수 - 이진수 코드를 편의상 8/16진수 형태로 표현한 내용
-
기호코드 - 사용자가 연산 부분, 주소 부분 등에 대해 기호(문자, 숫자, 특수문자 등)을 사용하게 되며, 각 기호 명령어는 하나의 이진 코드로 번역되는데 이러한 번역을 어셈블러(assembler)가 담당
-
고급 프로그래밍 언어 - 컴퓨터 하드웨어의 동작을 염두에 두지 않고(HW와 SW 사이의 독립성) 문제해결에 관점을 맞춰서 개발한 인간 중심의 언어 C, C#, Java 등이 대표적인 사용언어들이다. 이러한 언어를 컴파일러형 언어(complier language)라고 한다.
기계어와 프로그래밍 언어간 관계
기계어
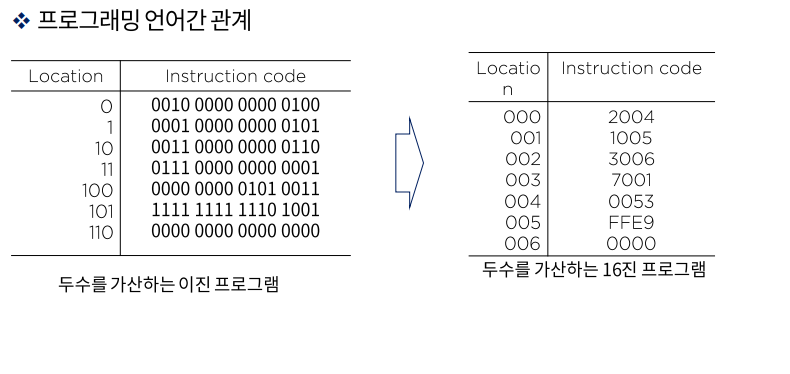
- 두 수를 가산하는 이진 프로그램
- 기계어 형태의 프로그램, 위치와 명령코드로 구성
- 두 수를 가산하는 16진 프로그램
- 이진 프로그램와 비교했을 때 보기 편하도록 만듦 (16비트를 4비트씩 잘라서 표현)
어셈블리어
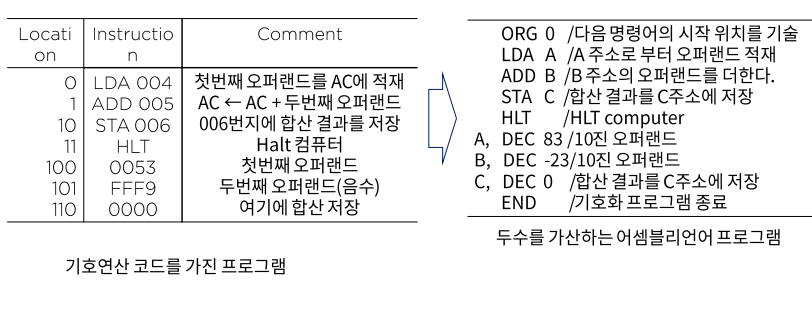
고급 언어

어셈블리어의 문법 규칙
- 라벨 필드 : 기호 주소를 나타내거나 빈칸이 될 수 있다.
- 기호 주소는 세 개 이하의 영자와 숫자들로 구성, 첫 자는 문자여야함
- 기호 주소는 세 개 이하의 영자와 숫자들로 구성, 첫 자는 문자여야함
- 명령어 필드 : 기계 명령어나 슈도 명령어를 기술
- 메모리 참조 명령어(MRI) - LOAD, ADD 등등
- 레지스터 참조 또는 입출력 명령어(non-MRI)
- 슈도 명령어 - ORG (다음 명령어의 시작 위치를 기술) 등등
- 코멘트 필드 : 명령어에 대한 주석이나 해설을 하거나 불필요할 경우 생략도 가능
프로그래밍 언어의 실행
프로그램 처리 과정
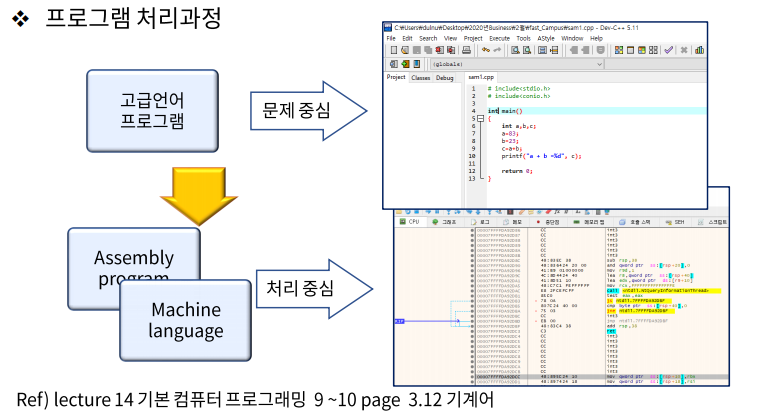
- 개발자는 CPU가 어떻게 명령어들을 처리하는지 신경 안 쓰고 문제를 해결하는데만 집중할 수 있다.
소프트웨어 개발 패러다임의 변화
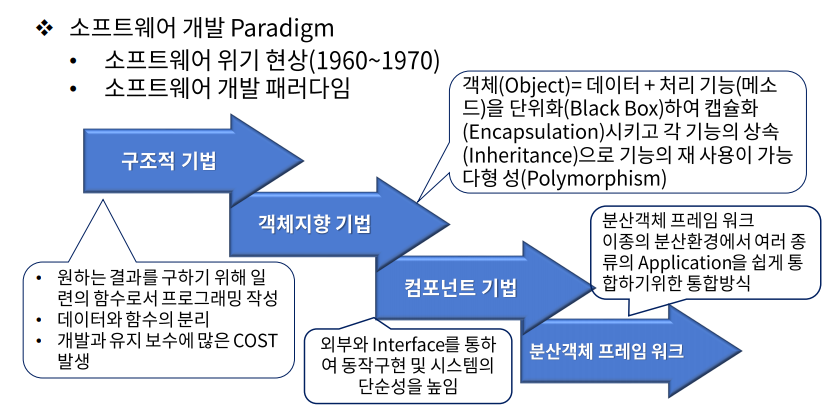
- 컴포넌트 기법 - 모듈별로 분리해서 집약시키는 기법
- 분산객체 프레임 워크 - 다른 환경의 Application을 호환성을 맞춰서 통합하는 방식 (클라우드 환경)
함수형 ㅇㄷ?
컴퓨터 네트워크 환경
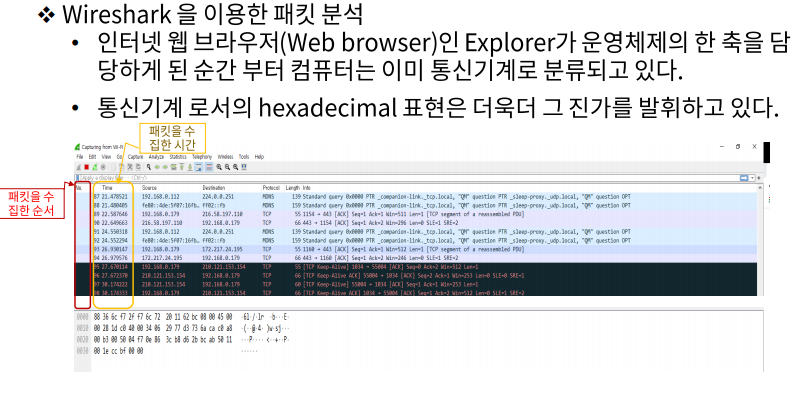
우리가 편하게 웹 서핑을 하거나, 게임을 할 때 이루어지는 통신은 모두 16진수(Hexadecimal) 표현으로 이루어진다.
데이터의 종속성 - 병렬 처리 그리고 파이프라인
병렬 처리 (parallel processing)
컴퓨터 시스템의 계산 속도 향상을 목적으로 하여 동시 데이터 처리 기능을 제공하는 광범위한 개념의 기술을 의미한다.
복잡도에 따른 병렬처리의 다양한 단계
-
사용 레지스터의 형태에 따른 병렬성 구현(ex - 시프트 레지스터, INPR, OUTR)
-
동일한 또는 서로 다른 동작을 동시에 수행하는 여러 개의 기능 장치(functional unit)를 가지고 데이터를 각각의 장치에 분산시켜 작업을 수행하는 경우
(ex - 산술, 논리, 시프트 동작을 세 개의 장치로 분류하고, 제어 장치의 관리에 따라 피 연산자를 각 장치들 사이에서 전환시킨다.)
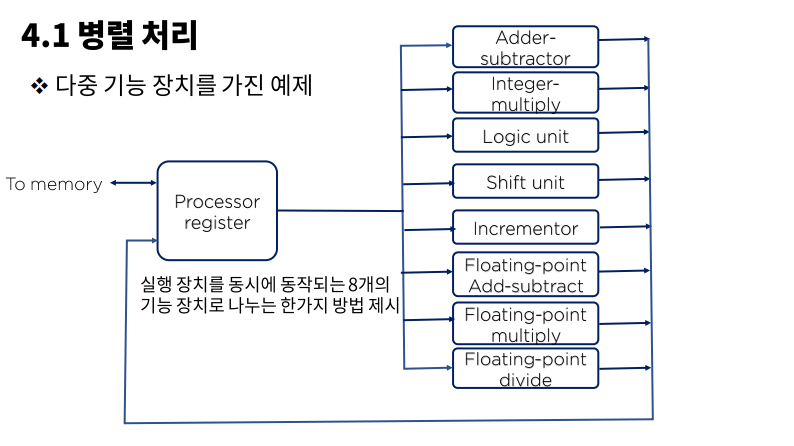
병렬 처리를 할 때 각각의 장치에 AC를 달아서 데이터를 누적시켜놓고
다른 장치가 그 데이터를 필요로 할 때 전송하는 로직이 이용되고 있다.
명령어 흐름과 데이터 흐름의 분류
동시에 처리되는 명령어와 데이터 항목 수에 의해 컴퓨터 시스템의 구조를 파악하는 분류 방법
명령어 흐름(Instruction stream) -> 메모리로부터 읽어온 명령어의 순서,
데이터 흐름(data stream) -> 데이터에 대해 수행되는 동작
- SISD -> 단일 명령어 흐름, 단일 데이터 흐름
- SIMD -> 단일 명령어 흐름, 다중 데이터 흐름
- MISD -> 다중 명령어 흐름, 단일 데이터 흐름
- MIMD -> 다중 명령어 흐름, 다중 데이터 흐름
| 분류 | 설명 |
|---|---|
| SISD | - 제어장치, 처리장치, 메모리 장치를 가지는 단일 컴퓨터 구조 - 명령어들은 순차적으로 실행되고, 병렬처리는 다중 기능 장치나 파이프라인 처리에 의해서 구현된다. |
| SIMD | - 공통의 제어장치 아래에 여러 개의 처리 장치를 두는 구조 - 모든 프로세서는 동일한 명령어를 서로 다른 데이터 항목에 대하여 실행시킬 수 있다. - 모든 프로세서가 동시에 메모리에 접근 할 수 있도록 다중 모듈을 가진 공유 메모리 장치가 필요하다. |
| MISD | 이론적으로만 연구 되고 있음 |
| MIMD | - 여러 프로그램을 동시에 수행하는 능력을 가진 컴퓨터 시스템 - 대부분의 다중 프로세서와 다중 컴퓨터 시스템이 이 범주에 속한다. - 듀얼 코어, 쿼드 코어가 있다. |
이 분류방식은 컴퓨터의 구조적 연계방식에 대한 고찰이기보다는 외양적 행동 양식을 강조한 분류방식이라고 볼 수 있다. 이 분류 방식에 적합하지 않은 것이 파이프라인이다.
파이프라인
파이프라인의 구조와 성능
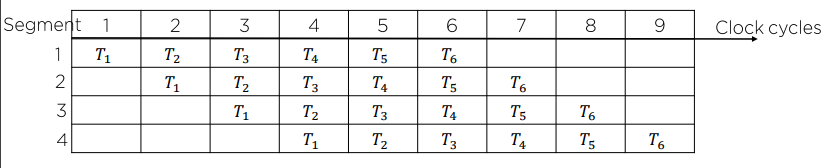
- Segment - 반복 횟수
- Clock cycles - 단계가 끝나는 시간 (가장 오래 걸리는 단계를 기준으로 삼는다.)
예를 들어 세탁, 건조, 다림질, 옷장에 넣기를 한다고 가정하자.
모든 옷을 세탁하고,
세탁된 모든 옷을 건조하고,
건조된 모든 옷을 다림질하고,
다림질된 모든 옷을 옷장에 넣는 방식이 아니라
옷 하나씩 각 단계를 순차적으로 돌리는 방법이다.
그러면 세탁 끝나고 건조할 때 세탁은 놀고있으니 바로 다음 옷을 투입하는 방식으로 진행된다.
이 일련의 단계에서 가장 오래 걸리는 단계를 클럭 사이클로 정의한다.
왜냐하면 제일 빠른 단계가 끝나도 다음 단계로 넘어가려면 전체 작업이 끝나야하기 때문이다.
예를 들어 건조가 끝났어도 세탁이 안 끝나면 다음 옷을 투입시키지 못한다.
파이프라인을 이용한 소요 시간
- 클럭 사이클 시간:
tp - 세그먼트:
k - 테스크의 개수:
n
첫 번째 테스크 t1은 동작 완료까지 k * tp 만큼의 시간이 걸리고
나머지 (n - 1)개의 테스크는 t1이 완료되고 나서 순차적으로 완료되니 (n - 1) * tp의 소요시간이 걸린다.
고로 소요 시간은 k * tp + (n - 1) * tp = (k + n - 1) * tp 만큼 걸리고
총 클럭 사이클은 (k + n - 1)이 된다.
비 파이프라인과 비교한 속도 증가율
비 파이프라인일 때
- 각 테스크를 완료하기 위한 시간:
tn - n개의 테스크에 대한 전체 수행 시간:
n * tn
위와 같이 정의되고
증가율 공식은 비 파이프라인 소요시간 / 파이프라인 소요시간로 정의 된다.
계산을 해보면
S(증가율) = n * tn / (k + n - 1) * tp
이 상태에서 limit(n -> 무한)을 해보면 (테스크가 무한히 증가)
S = tn / tp 가 된다.
이 때, 한 테스크의 수행시간이 같다고 하면 tn = k * tp로 정의가 된다. (위 사진 참고)
그러면 s = k * tp / tp = k
즉, 파이프 라인의 최대 속도 증가율은 세그먼트의 수 k라고 할 수 있다.
파이프라인 구조 - 데이터/구조
파이프라인의 구현
-
하나의 프로세스를 서로 다른 기능(function)을 가진 여러 개의 서브프로세스(subprocess)로 나누어 각 프로세스가 동시에 서로 다른 데이터로 취급하도록 하는 기법
-
각 세그먼트(segment)에서 수행된 연산 결과를 다음 세그먼트로 연속적으로 넘어가게 되어 데이터가 마지막 세그먼트를 통과하게 되면 최종적인 연산 결과를 얻게 된다.
- 하나의 프로세스를 다양한 연산으로 중복시킬 수 있는 근간은 각 세그먼트마다의 레지스터이다.
세그먼트 단위로 진행되는 중간 결과값은 레지스터에 저장되고 클락 펄스 신호를 주면 다음 세그먼트나 프로세스에게 전달해준다.

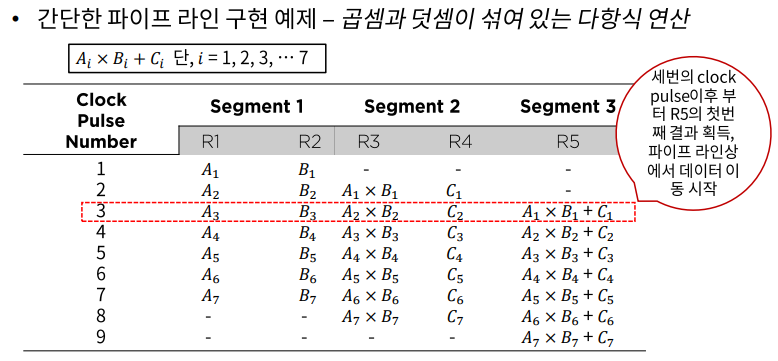
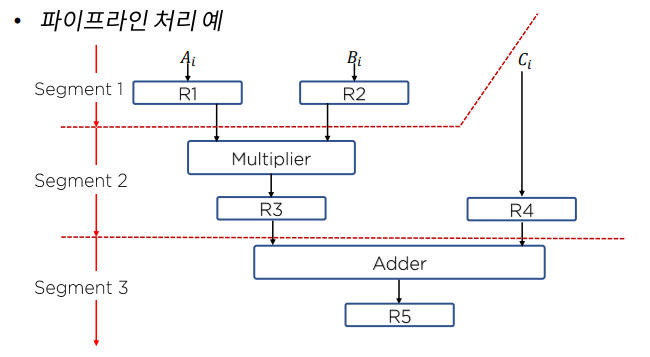
- 하나의 프로세스를 다양한 연산으로 중복시킬 수 있는 근간은 각 세그먼트마다의 레지스터이다.
- ALU가 작업할 수 있도록 Ai와 Bi를 각각 레지스터에 로드한다.
- R1과 R2에 저장된 값을 곱한 값을 R3에 저장하고 Ci를 R4에 로드한다.
- R3와 R4에 저장된 값을 서로 더해서 R5에 저장한다.
파이프라인의 일반적 고찰
- 각 세그먼트끼리 처리되는 속도가 비슷해야 효과적이다.
- 파이프라인은 반복되는 작업에 효과적이다