1. 문제
문제 설명
로봇개발자 "무지"는 한 달 앞으로 다가온 "카카오배 로봇경진대회"에 출품할 로봇을 준비하고 있습니다. 준비 중인 로봇은 2 x 1 크기의 로봇으로 "무지"는 "0"과 "1"로 이루어진 N x N 크기의 지도에서 2 x 1 크기인 로봇을 움직여 (N, N) 위치까지 이동 할 수 있도록 프로그래밍을 하려고 합니다. 로봇이 이동하는 지도는 가장 왼쪽, 상단의 좌표를 (1, 1)로 하며 지도 내에 표시된 숫자 "0"은 빈칸을 "1"은 벽을 나타냅니다. 로봇은 벽이 있는 칸 또는 지도 밖으로는 이동할 수 없습니다. 로봇은 처음에 아래 그림과 같이 좌표 (1, 1) 위치에서 가로방향으로 놓여있는 상태로 시작하며, 앞뒤 구분없이 움직일 수 있습니다.
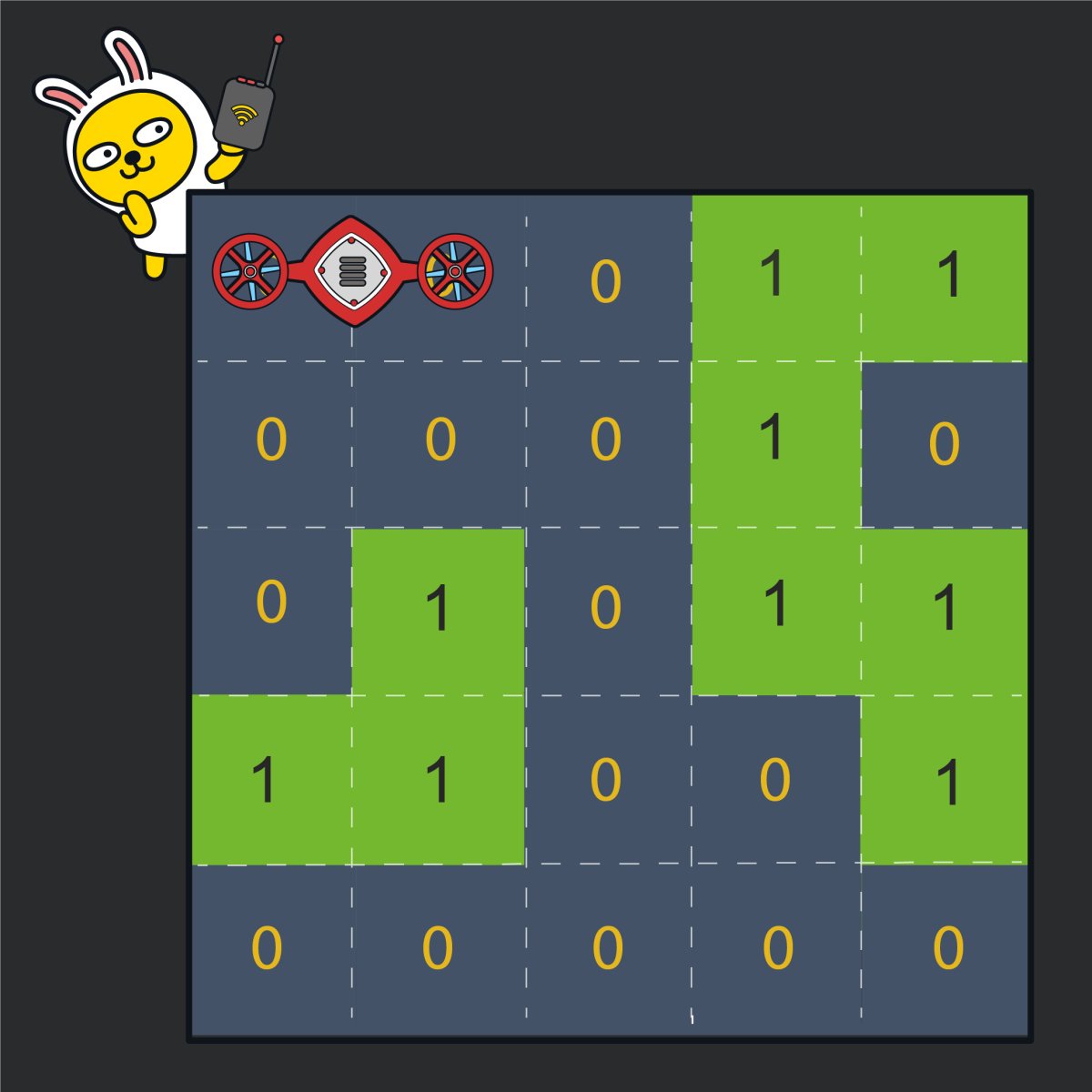
로봇이 움직일 때는 현재 놓여있는 상태를 유지하면서 이동합니다. 예를 들어, 위 그림에서 오른쪽으로 한 칸 이동한다면 (1, 2), (1, 3) 두 칸을 차지하게 되며, 아래로 이동한다면 (2, 1), (2, 2) 두 칸을 차지하게 됩니다. 로봇이 차지하는 두 칸 중 어느 한 칸이라도 (N, N) 위치에 도착하면 됩니다.
로봇은 다음과 같이 조건에 따라 회전이 가능합니다.
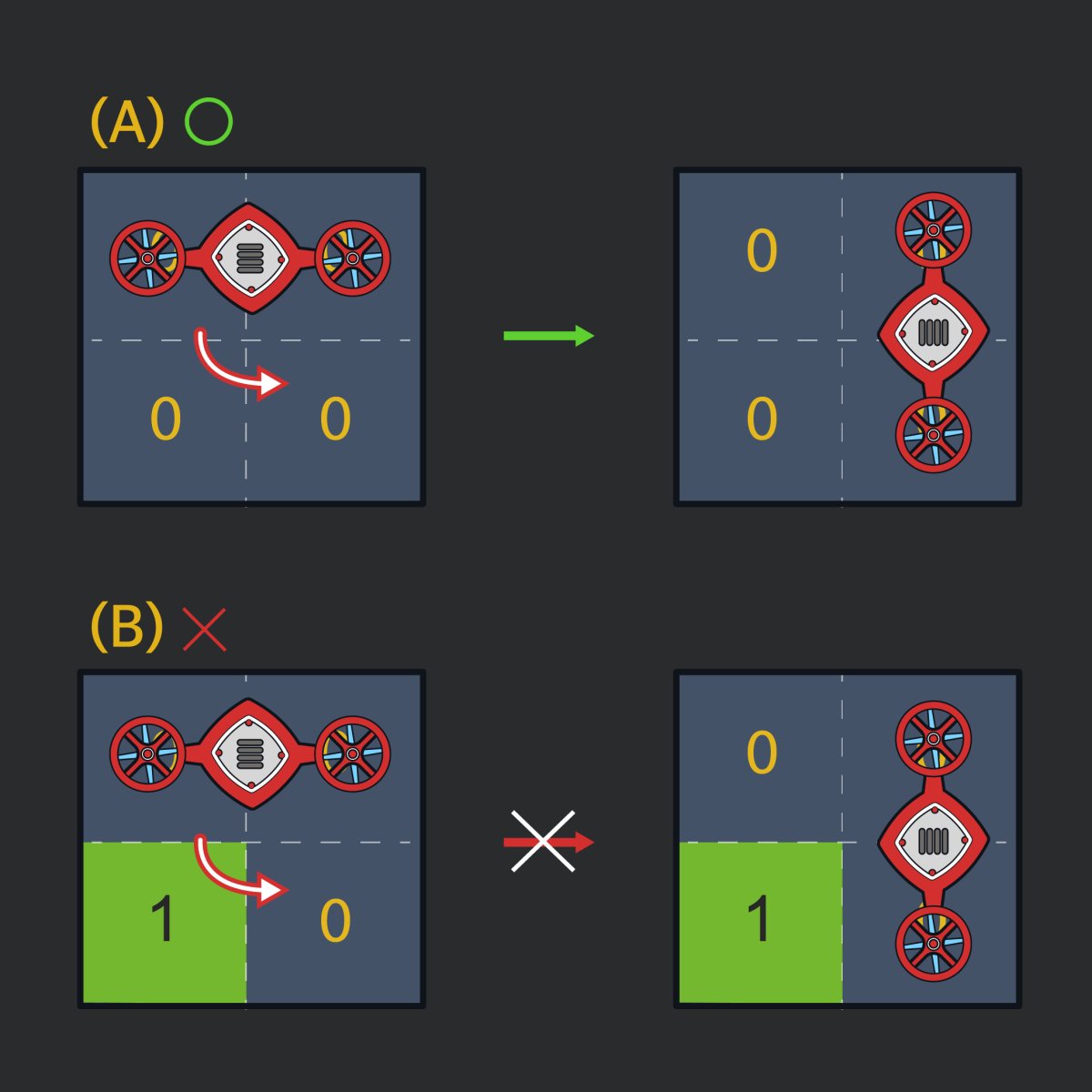
위 그림과 같이 로봇은 90도씩 회전할 수 있습니다. 단, 로봇이 차지하는 두 칸 중, 어느 칸이든 축이 될 수 있지만, 회전하는 방향(축이 되는 칸으로부터 대각선 방향에 있는 칸)에는 벽이 없어야 합니다. 로봇이 한 칸 이동하거나 90도 회전하는 데는 걸리는 시간은 정확히 1초 입니다.
"0"과 "1"로 이루어진 지도인 board가 주어질 때, 로봇이 (N, N) 위치까지 이동하는데 필요한 최소 시간을 return 하도록 solution 함수를 완성해주세요.
제한사항
board의 한 변의 길이는 5 이상 100 이하입니다.
board의 원소는 0 또는 1입니다.
로봇이 처음에 놓여 있는 칸 (1, 1), (1, 2)는 항상 0으로 주어집니다.
로봇이 항상 목적지에 도착할 수 있는 경우만 입력으로 주어집니다.
2. 풀이
2-1. 조건
- 로봇은 현재 놓여있는 상태를 유지하면서 이동한다.
- 로봇은 90도로 회전이 가능하다. (단 회전 축이 되는 칸에 벽이 없어야한다)
2-2. 풀이
이 문제는 얼핏봐도 bfs를 이용해서
(N, N) 좌표에 도착했을 때 소요한 탐색 횟수를 리턴하면 되겠죠?
상태 공간은 로봇이 차지하는 좌표가 두 칸이니
(로봇의 왼쪽 몸체 좌표, 로봇의 오른쪽 몸체 좌표, 이동 횟수) 로 정의할 수 있습니다.
남은 부분은 로봇의 회전인데 구현하기 조금 까다로워 보입니다.
하지만 현재 로봇이 가로로 있는지, 세로로 있는지 분기를 나누고
회전하는 축에 벽이 없을 때 (2번 조건)
가로로 있을 땐 위쪽, 아래쪽으로 회전
세로로 있을 땐 왼쪽, 오른쪽으로 회전시킨 다음 좌표로 상태 공간을 추가하면 되겠죠?
(자세한 부분은 코드를 봅시다)
다시 총 정리를 해보면
1. bfs를 이용해서 로봇을 이동
2. 북, 동, 남, 서 방향 이동과 회전까지 고려해서 다음 상태 공간 추가
3. (N, N) 도착시 탐색 횟수 리턴
3. 전체 코드
import java.util.LinkedList;
import java.util.Queue;
class Solution {
static int N;
static int[][] map;
static boolean[][][][] visit;
public int solution(int[][] board) {
N = board.length;
map = board;
visit = new boolean[N][N][N][N];
int[] my = { -1, 0, 1, 0 }, mx = { 0, 1, 0, -1 };
Queue<int[]> q = new LinkedList<>();
add(0, 0, 0, 1, 0, q);
while (!q.isEmpty()) {
int[] cur = q.poll();
/**
* 4방향 탐색
*/
for (int dir = 0; dir < 4; dir++) {
int ny1 = cur[0] + my[dir], nx1 = cur[1] + mx[dir], ny2 = cur[2] + my[dir], nx2 = cur[3] + mx[dir];
// 갈 수 있을 때
if (isRange(ny1, nx1) && isRange(ny2, nx2) && isNotObstacle(ny1, nx1, ny2, nx2) && !visit[ny1][nx1][ny2][nx2]) {
if (isArrive(ny1, nx1, ny2, nx2)) return cur[4] + 1;
add(ny1, nx1, ny2, nx2, cur[4] + 1, q);
}
}
/**
* 로봇 회전
*/
if (cur[0] == cur[2]) { // 가로로 있을 때
// 위로 회전
int y = cur[0] - 1;
// 범위에 들고 회전 축에 벽이 없을 때 (2번 조건)
if (isRange(y, cur[1]) && isNotObstacle(y, cur[1], y, cur[3])) {
if (!visit[y][cur[3]][cur[2]][cur[3]]) {
add(y, cur[3], cur[2], cur[3], cur[4] + 1, q);
}
if (!visit[y][cur[1]][cur[0]][cur[1]]) {
add(y, cur[1], cur[0], cur[1], cur[4] + 1, q);
}
}
// 아래로 회전
y = cur[0] + 1;
if (isRange(y, cur[1]) && isNotObstacle(y, cur[1], y, cur[3])) {
if (!visit[y][cur[3]][cur[2]][cur[3]]) {
if (isArrive(y, cur[3], cur[2], cur[3])) return cur[4] + 1;
add(y, cur[3], cur[2], cur[3], cur[4] + 1, q);
}
if (!visit[y][cur[1]][cur[0]][cur[1]]) {
if (isArrive(y, cur[1], cur[0], cur[1])) return cur[4] + 1;
add(y, cur[1], cur[0], cur[1], cur[4] + 1, q);
}
}
}
else { // 세로로 있을 때
// 왼쪽으로 회전
int x = cur[1] - 1;
if (isRange(cur[2], x) && isNotObstacle(cur[2], x, cur[0], x)) {
if (!visit[cur[0]][x][cur[0]][cur[1]]) {
add(cur[0], x, cur[0], cur[1], cur[4] + 1, q);
}
if (!visit[cur[2]][x][cur[2]][cur[3]]) {
add(cur[2], x, cur[2], cur[3], cur[4] + 1, q);
}
}
// 오른쪽으로 회전
x = cur[1] + 1;
if (isRange(cur[2], x) && isNotObstacle(cur[2], x, cur[0], x)) {
if (!visit[cur[0]][cur[1]][cur[0]][x]) {
if (isArrive(cur[0], cur[1], cur[0], x)) return cur[4] + 1;
add(cur[0], cur[1], cur[0], x, cur[4] + 1, q);
}
if (!visit[cur[2]][cur[3]][cur[2]][x]) {
if (isArrive(cur[2], cur[3], cur[2], x)) return cur[4] + 1;
add(cur[2], cur[3], cur[2], x, cur[4] + 1, q);
}
}
}
}
return -1;
}
// 범위 안에 드는지 여부
static boolean isRange(int y, int x) {
return 0 <= y && y < N && 0 <= x && x < N;
}
// 장애물이 아닌지 여부
static boolean isNotObstacle(int y1, int x1, int y2, int x2) {
return map[y1][x1] != 1 && map[y2][x2] != 1;
}
// 도착 여부
static boolean isArrive(int y1, int x1, int y2, int x2) {
return (y1 == N - 1 && x2 == N - 1) || (y2 == N - 1 && x2 == N - 1);
}
// 다음 상태 공간 add
static void add(int y1, int x1, int y2, int x2, int n, Queue<int[]> q) {
q.add(new int[] { y1, x1, y2, x2, n });
visit[y1][x1][y2][x2] = visit[y2][x2][y1][x1] = true;
}
}
(N, N) 에 도착하는 순간은 동쪽, 남쪽으로 이동하거나,
아래쪽, 오른쪽으로 회전할 때만 신경쓰면 됩니다.