1. 문제
문제
N x N 크기인 정사각 격자 형태의 지형이 있습니다. 각 격자 칸은 1 x 1 크기이며, 숫자가 하나씩 적혀있습니다. 격자 칸에 적힌 숫자는 그 칸의 높이를 나타냅니다.
이 지형의 아무 칸에서나 출발해 모든 칸을 방문하는 탐험을 떠나려 합니다. 칸을 이동할 때는 상, 하, 좌, 우로 한 칸씩 이동할 수 있는데, 현재 칸과 이동하려는 칸의 높이 차가 height 이하여야 합니다. 높이 차가 height 보다 많이 나는 경우에는 사다리를 설치해서 이동할 수 있습니다. 이때, 사다리를 설치하는데 두 격자 칸의 높이차만큼 비용이 듭니다. 따라서, 최대한 적은 비용이 들도록 사다리를 설치해서 모든 칸으로 이동 가능하도록 해야 합니다. 설치할 수 있는 사다리 개수에 제한은 없으며, 설치한 사다리는 철거하지 않습니다.
각 격자칸의 높이가 담긴 2차원 배열 land와 이동 가능한 최대 높이차 height가 매개변수로 주어질 때, 모든 칸을 방문하기 위해 필요한 사다리 설치 비용의 최솟값을 return 하도록 solution 함수를 완성해주세요.
제한사항
land는 N x N크기인 2차원 배열입니다.
land의 최소 크기는 4 x 4, 최대 크기는 300 x 300입니다.
land의 원소는 각 격자 칸의 높이를 나타냅니다.
격자 칸의 높이는 1 이상 10,000 이하인 자연수입니다.
height는 1 이상 10,000 이하인 자연수입니다.
입출력 예 설명
입출력 예 #1
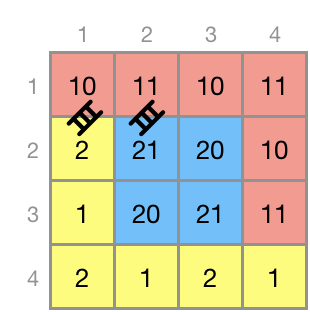
각 칸의 높이는 다음과 같으며, 높이차가 3 이하인 경우 사다리 없이 이동이 가능합니다.
위 그림에서 사다리를 이용하지 않고 이동 가능한 범위는 같은 색으로 칠해져 있습니다. 예를 들어 (1행 2열) 높이 4인 칸에서 (1행 3열) 높이 8인 칸으로 직접 이동할 수는 없지만, 높이가 5인 칸을 이용하면 사다리를 사용하지 않고 이동할 수 있습니다.
따라서 다음과 같이 사다리 두 개만 설치하면 모든 칸을 방문할 수 있고 최소 비용은 15가 됩니다.
높이 5인 칸 → 높이 10인 칸 : 비용 5
높이 10인 칸 → 높이 20인 칸 : 비용 10
입출력 예 #2
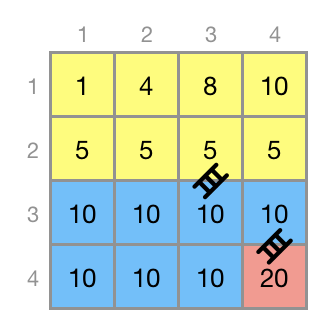
각 칸의 높이는 다음과 같으며, 높이차가 1 이하인 경우 사다리 없이 이동이 가능합니다.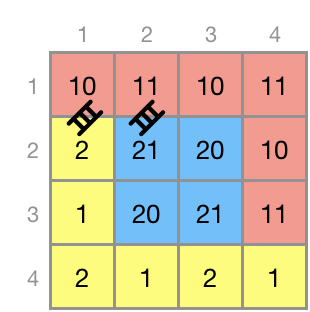
위 그림과 같이 (2행 1열) → (1행 1열), (1행 2열) → (2행 2열) 두 곳에 사다리를 설치하면 설치비용이 18로 최소가 됩니다.
2. 풀이
2-1. 조건
- 현재 칸과 이동하려는 칸의 높이 차가 height이하여야 한다.
- 높이 차가 height보다 크면 두 격자 칸의 높이 차만큼 비용을 지불하고 이동할 수 있다.
2-2. 풀이
이 문제는 어떤 식으로 풀어야 할까요?
단순히 주먹구구식으로 모든 구역에 사다리를 설치해보고
bfs를 통해 모든 칸을 방문할 수 있는지 확인해보는 방법이 있지만
사다리를 설치하는 경우의 수가 적어도 N! 이기 때문에 사실상 불가능하겠죠?
조금 더 효율적이고 깔끔한 방식을 생각해보죠.
입출력 예제2번의 사진을 보면 빨강, 노랑, 파랑색의 영역은
사다리를 설치하지 않아도 서로 이동할 수 있는 영역입니다.
여기서 우리는 서로 이동할 수 있는 영역들을 정점이라 생각하고
정점간의 이어주는 사다리를 엣지라고 생각해봅시다.
이때 우리는 모든 정점을 최소 사다리 설치 비용으로 이어주는
최소 스패닝 트리(MST) 문제라는 사실을 알 수 있습니다.
저는 크루스칼 알고리즘으로 이 문제를 해결해보겠습니다.
다시 총 정리를 해보면
1. bfs를 통해 서로 이동할 수 있는 영역을 나눠줍니다.
2. 사다리 리스트에 영역과 영역 사이에 설치할 수 있는 사다리들을 담아줍니다.
3. 크루스칼 알고리즘을 이용해 사다리를 설치하는 최소 비용을 구합니다.
3. 전체 코드
function solution(land, height) {
const N = land.length;
const moves = [[-1, 0], [0, 1], [1, 0], [0, -1]];
const q = [];
const areas = [...Array(N)].map(_ => [...Array(N)].map(_ => 0));
let area = 1;
const is_out_of_range = (y, x) => (y < 0 || y >= N || x < 0 || x >= N);
// 1. bfs를 통해 서로 이동할 수 있는 영역 나누기 (1번 계획)
land.forEach((row, y) => {
row.forEach((cur_height, x) => {
if (!areas[y][x]) {
q.push([y, x]);
areas[y][x] = area;
while (q.length) {
const [y, x] = q.shift();
for (const [my, mx] of moves) {
const ny = y + my;
const nx = x + mx;
// 영역 밖일 때
if (is_out_of_range(ny, nx)) continue;
// 지금 칠하고 있는 영역일 때
if (areas[ny][nx]) continue;
// 칠하고자 하는 칸과 현재 있는 칸 차이가 height보다 클 때
if (Math.abs(land[y][x] - land[ny][nx]) > height) continue;
q.push([ny, nx]);
areas[ny][nx] = area;
}
}
area++;
}
});
});
/**
* 크루스칼 알고리즘 구현에 필요한 리스트와 union-find 함수들
*/
const set = [...Array(area)].map((_, i) => i);
const find = a => (set[a] = set[a] == a ? a : find(set[a]));
const union = (a, b) => {
a = find(a);
b = find(b);
a > b ? set[a] = b : set[b] = a;
};
const is_same_parent = (a, b) => (find(a) == find(b));
return (
areas
// 2. 영역과 영역 사이에 설치할 수 있는 사다리들을 담는다. (2번 계획)
.reduce((m, row, y) => {
return row.reduce((m, area, x) => {
for (const [my, mx] of moves) {
const ny = y + my;
const nx = x + mx;
// 영역 밖일 때
if (is_out_of_range(ny, nx)) continue;
// 같은 영역일 때
if (area == areas[ny][nx]) continue;
// 사다리를 담아준다. [설치 비용, 영역1, 영역2]
m.push([Math.abs(land[y][x] - land[ny][nx]), area, areas[ny][nx]]);
}
return m;
}, m);
}, [])
// 3. 크루스칼 알고리즘으로 최소 비용 리턴 (3번 계획)
.sort(([a], [b]) => a - b) // 설치 비용을 오름차순으로 정렬
.reduce((m, [cost, a, b]) => {
// 부모 노드가 같을 때
if (is_same_parent(a, b)) return m;
// 정점 이어주기
union(a, b);
// 설치 비용 누적
return m += cost;
}, 0)
);
}