프로그래머스 - 소수 찾기

1. 문제

설명
한자리 숫자가 적힌 종이 조각이 흩어져있습니다. 흩어진 종이 조각을 붙여 소수를 몇 개 만들 수 있는지 알아내려 합니다.

각 종이 조각에 적힌 숫자가 적힌 문자열 numbers가 주어졌을 때, 종이 조각으로 만들 수 있는 소수가 몇 개인지 return 하도록 solution 함수를 완성해주세요.

제한사항

• numbers는 길이 1 이상 7 이하인 문자열입니다.
• numbers는 0~9까지 숫자만으로 이루어져 있습니다.
• "013"은 0, 1, 3 숫자가 적힌 종이 조각이 흩어져있다는 의미입니다.

입출력 예

numbers	return
"17"	3
"011"	2

입출력 예 설명

예제 #1
[1, 7]으로는 소수 [7, 17, 71]를 만들 수 있습니다.

예제 #2
[0, 1, 1]으로는 소수 [11, 101]를 만들 수 있습니다.

• 11과 011은 같은 숫자로 취급합니다.

2. 풀이

모든 숫자의 순열을 만들어서 소수인지 판별한 다음 개수를 세면 됩니다.

계획 1 - 모든 숫자의 순열을 만듭니다.

        for (let i = 0; i < N; i++) {
            if (isUsed[i]) continue; 

            isUsed[i] = 1;
            f(depth + 1, number + numbers[i]);
            isUsed[i] = 0;
        }

이미 사용한 숫자일 때는 넘어가면서 재귀 호출로 순열을 만듭니다.

예시로 "183"이 input으로 들어왔을 때
재귀 함수는 이런 모양으로 작동하며 순열을 만듭니다.

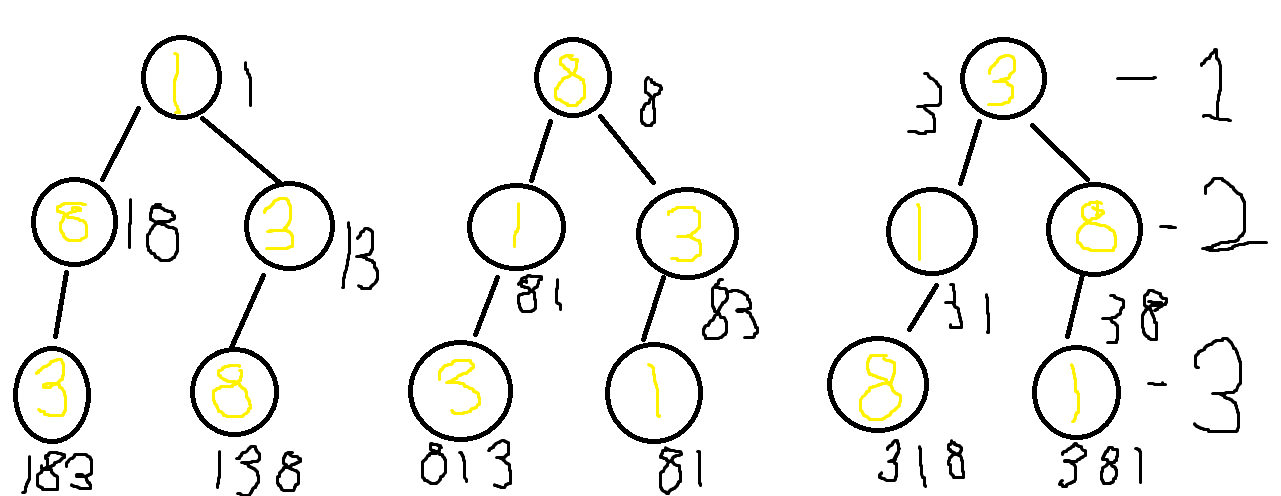
숫자를 탐색하며 현재까지 만든 숫자에 탐색한 숫자를 붙여주며 순열을 만듭니다.
이 그림으로 알 수 있듯이 깊이가 0보다 클 때 만든 숫자가 소수인지 판별하면 됩니다.

계획 2 - 소수 판별하기

    const isPrime = (number) => {
        if (number <= 1) return false;

        const sqrt = Math.sqrt(number);

        for (let i = 2; i <= sqrt; i++) {
            if (number % i == 0) return false;
        }

        return true;
    };

숫자를 2부터 숫자의 제곱근까지 나눠봐서 하나라도 나뉘어 떨어지는지 확인하면 됩니다.
끝까지 나누지 않고 제곱근까지 나눠도 소수를 판별할 수 있는 이유는
숫자의 약수는 숫자의 제곱근 범위에 존재하기 때문입니다.
예시로 숫자가 12일 때 2 x 6, 3 x 4, 4 x 3, 6 x 2로 표현되고
몫이 커지면 나누는 값이 작아지거나, 나누는 값이 커지면 몫이 작아지는 반비례 관계입니다.
즉, 제곱근까지 나누어보면 이후에는 몫과 나누는 값이 반대로 바뀌는 경우밖에 없으므로
굳이 나누어보지 않아도 됩니다.

3. 전체 코드

function solution(numbers) {
    const N = numbers.length;
    const judged = {}; // 중복해서 세지 않도록 소수라고 판별한 숫자를 저장
    const isUsed = [...Array(N)].map(() => 0);
    let ans = 0;

    // 계획 2 - 소수 판별하기
    const isPrime = (number) => {
        if (number <= 1) return false;

        const sqrt = Math.sqrt(number);

        for (let i = 2; i <= sqrt; i++) {
            if (number % i == 0) return false;
        }

        return true;
    };

    // 계획 1 - 모든 숫자의 순열을 만듭니다.
    (function f(depth, number) {    
        // 깊이가 0보다 클 때 숫자 순열이 만들어집니다.
        if (depth > 0) {
            const parseNumber = Number(number);

            if (!judged[parseNumber] && isPrime(parseNumber)) {
                ans++;
                judged[parseNumber] = 1;
            }
        }

        if (depth == N) return;

        for (let i = 0; i < N; i++) {
            if (isUsed[i]) continue;

            isUsed[i] = 1;
            f(depth + 1, number + numbers[i]);
            isUsed[i] = 0;
        }
    })(0, '');

    return ans;
}