Index
책에는 인덱스가 있습니다. 인덱스를 적어두면 몇 페이지를 더 사용하지만 해당 내용과 관련된 부분을 빠르게 찾을 수 있습니다. 순서대로 찾아보는 경로 외에 다른 경로를 제공하는 것입니다(secondary access path). 컴퓨터 파일을 검색하는데도 인덱스를 이용할 수 있습니다. 인덱스는 인덱스 필드(키 값)를 이용해 빠르게 레코드들을 검색하기 위해 사용하는 보조 접근 구조(access structure)입니다. 인덱스를 구현하는 방법 중 한 가지로 B Tree, B+ Tree를 이용하는 방법이 있습니다. B Tree를 이용하면 인덱스가 필요하면 생성하고, 필요없으면 삭제할 수 있습니다.
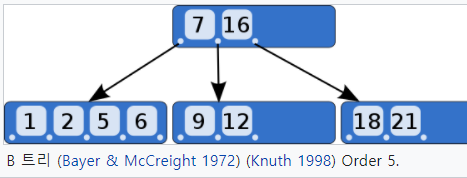
B Tree
2진 트리에서는 트리의 높이가 높아지는 문제가 있습니다. 균형을 맞춰서 높이는 낮출 수 있었지만 균형을 맞추는데 비용이 많이 들었습니다. Multiway Search Tree는 2진 트리의 일반적인 형태로 한 노드 안에 여러 데이터를 가질 수 있도록 만든 것입니다. 한 노드 안의 값들은 정렬되어 있도록 합니다. 탐색은 2진 트리에서처럼 진행할 수 있습니다.
B Tree는 Multiway Search Tree의 한 종류입니다. 트리의 균형을 더 효율적으로 유지하기 위해 트리의 각 노드(내부 노드)는 50퍼센트 이상(ceil(n/2))은 채워놓자는 조건을 추가했습니다.(루트 노드는 제외입니다.) leaf 노드는 ceil(n/2)-1개 이상을 가져야 합니다. 마지막으로 모든 leaf 노드는 같은 레벨에 있어야 하는 제약 조건을 추가했습니다.
이렇게 B Tree를 만들면 트리의 높이는 2진 트리보다 더 낮아집니다. 균형을 맞추는 연산도 대부분의 경우 간단하게 해결이 됩니다.
B Tree에 데이터 추가
2가지 동작이 필요할 수 있습니다.
add on leaf, split(balancing)
- 추가할 위치 찾기
2진 탐색 트리처럼 찾을 수 있습니다.
추가될 위치는 항상 leaf 노드가 될 것입니다. - 저장과 분할
만약 찾은 노드에 채워넣을 때 50~100퍼센트 채워진 조건을 만족하면 채워넣습니다. 문제가 되는 경우는 모자라거나 넘칠 때입니다. 모자라는 경우는 없습니다. 넘치게 되는 경우 분할(split)을 해서 균형을 맞춥니다. 분할은 먼저 넘치도록 추가했다고 치고 median을 부모 노드로 올립니다. median보다 작은 부분과 큰 부분을 각각 노드를 만듭니다. median 좌측 트리포인터가 median보다 작은 부분을 가르키도록 합니다. median 우측트리포인터는 median보다 큰 부분을 가르키도록 합니다. 부모노드가 다시 넘치면 부모노드도 분할을 적용합니다. 루트노드까지 도달하면 트리의 높이는 1증가하게 됩니다.
B Tree에서 데이터 삭제
-
삭제할 데이터 찾기
2진 탐색 트리처럼 찾을 수 있습니다.
삭제할 데이터가 내부 노드인지 leaf 노드인지에 따라 다르게 처리합니다. -
삭제
삭제할 노드가 leaf 노드이면 우선 삭제합니다. 균형 조건을 위배하면 왼쪽/오른쪽 형제 노드에게 빌립니다. 그것마저 안 되면 부모노드에서 공통인 수를 내리고 두 형제 노드를 합칩니다.
leaf 노드가 아니면 우선 삭제합니다. 그리고 나서 해당 노드의 왼쪽 트리포인터가 가리키는 서브트리의 가장 오른쪽 수로 대체합니다. 대체된 수는 삭제된 수보다 작은 수 중에 가장 큰 수 입니다. 균형이 안 맞으면 균형을 맞춰줍니다.
B+ 트리
B트리와 달리 B+트리는 데이터를 leaf 노드에만 저장합니다. 내부 노드는 탐색할 수 있도록 키값과 트리포인터만 가지고 있습니다. B+ 트리의 leaf노드들은 서로 연결되어 있습니다. 그래서 데이터의 순차적 접근에 B 트리보다 더 유리합니다.