is prime?

소수의 정의를 이용한 판별

소수는 1과 자기 자신만을 약수로 가지는 수입니다. 소수의 정의에 따라 소수인지 아닌지를 검사할 수 있습니다. 약수를 모두 구하고 약수의 갯수가 2개(1과 자기자신)이면 소수가 됩니다. 약수는 쌍으로 존재합니다. 그 쌍들 중 작은 것들은 모두 그 수의 제곱근 값 이하입니다. 따라서 어떤 수의 모든 약수는 제곱근 시간 안에 구할 수 있습니다.

	int n; cin >> n;
	int cnt = 0;
	for(int i=1; i * i <= n; i++){
		if(n % i == 0){
			cnt++;
			if(i != n-i) cnt++;
		}
	}
	
	cout<<(cnt!=2 ? "not ":"")<<"prime number\n";
	

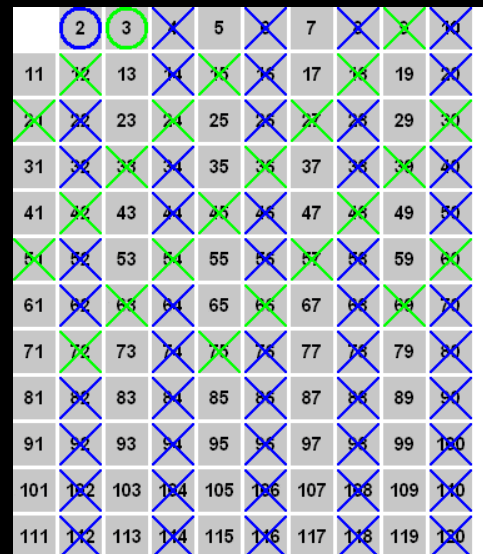
에라토스테네스 체를 이용한 판별

에라테네테네스의 체를 이용해서 어떤 수 이하의 모든 소수를 거의 O(n)만에 구할 수 있습니다. 정확히는 O(nloglogn)이라고 합니다. 많은 수의 소수 여부를 판별한다면 첫번째 방법보다 유리할 것입니다. 하지만 소수 하나를 구할 것이라면 소수의 정의를 이용해서 구하는게 더 나을 것입니다. 그리고 수가 천만보다 큰 수준이면 에라토스테네스의 체 방법은 메모리 부족으로 사용하기 힘들어집니다.

facorization

O(n*sqrt(n))

n 이하의 소수를 모두 구하고, 그 소수들이 n에 몇개씩 들어있는지 확인하면 소인수 분해를 할 수 있습니다. 쉽게 떠올릴 수 있는 방법이지만 조금 느린 방법입니다.

	int n; cin>>n;
	vector<int> primes;
	for(int i=2; i <= n; i++){
		bool isprime=true;
		for(int j=2; j * j <= i; j++){
			if(i%j == 0) isprime=false;
		}
		
		if(isprime) primes.push_back(i);
	} 
	
	vector<int> factors;
	for(ll p:primes){
		if(n == 1) break;
		for(;n!=1 && n%p == 0;n /= p) factors.push_back(p);
	}
	
	for(int f : factors) cout<<f<<" "; cout<<'\n';

에라토스테네스 체를 이용

에라토스테네스의 체를 이용해서 어떤 수 이하의 소수들을 모두 구해놓고 각 소수로 나눠질 때까지 나눠보면 소인수 분해를 할 수 있습니다. 에라토스테네스의 체를 만드는 데 시간이 O(n)정도 걸립니다. 하지만 각 수를 나눠보는 것은 그리 오래 걸리지 않습니다.(아마 log(n) 수준 또는 loglog(n)수준인 것 같습니다.) 소수인지 판별할 때와 마찬가지로 여러 수에 대한 답을 할 때 사용하면 유리합니다.

//global
	const int MAX=1e7;
	int isprime[MAX];
    
//local
	vector<int> primes;
	int n; cin>>n;
	
	function<void()> eratos=[&](){
		for(int i=2;i<=n;i++){
			if(isprime[i]) continue;
			isprime[i]=1;
			primes.push_back(i);
			for(int j=i*2;j<=n;j+=i) isprime[j]=-1;
           		 //isprime[j]=-1입니다. isprime[i]로 실수하기 쉽습니다.
		}
		return;	
	};
	
	eratos();
	vector<int> factors;
	
	for(int p:primes){
		if(p>n || n==1) break;
		for(;n!=1 && n%p==0; n/=p) factors.push_back(p);
	}
	
	for(int f:factors) cout<<f<<" "; cout<<'\n';	

minimum factor를 구해놓기

어떤 수가 들어오든 그 수의 가장 작은 factor로 나누다 보면 자연스레 소인수분해가 됩니다. 구현은 에라토스테네스 체를 응응합니다. 단순히 에라토스테네스 체를 사용한 것보다 더 빠릅니다. 선형적으로 나눌 소수를 찾는 시간이 들지 않습니다. 나눠야 할 factor가 무엇인지 저장해 놓았기 때문입니다.

시간복잡도 : O(nloglogn)
마찬가지로 메모리가 많이 사용될 수 있습니다.
마찬가지로 여러 질의에 빠르게 대답할 수 있습니다.

//global
	const int MAX=1e7;
	int minfactor[MAX];
    
//local
	int n; cin>>n;
	
	function<void()> eratoslike =[&](){
		for(int i=2;i<=n;i++){
			if(minfactor[i]) continue;
			minfactor[i]=i;
			for(int j=i*2;j<=n;j+=i) minfactor[j]=i;
		}		
	};
	
	eratoslike();
	vector<int> factors;
	
	for(;n!=1;n/=minfactor[n]){
		factors.push_back(minfactor[n]);
	}
	for(int f:factors) cout<<f<<' '; cout<<'\n';

소수와 관련이 있는 문제