코드스테이츠에서 매일 알고리즘 풀때도 한문제 정도 밖에 못봤을 정도로 눈에 띄지는 않았던 DP 알고리즘이다. 프로그래머스에서도 출제빈도는 낮음으로 되어있다. 그렇지만 이번에 알고리즘 테스트에서 봤던 문제들이 둘다 DP가 나와서 공부한김에 정리 하고자 한다. 지금도 그렇고 예전도 그렇고 레퍼런스를 보고 들었던 생각은 참 신박하다..?
많이들 알고있는 피보나치 수열을 구하는 알고리즘에서 값을 저장하고 중복된 값을 다시 계산하지 않고 꺼내 쓰는 메모이제이션도 DP알고리즘이다.
DP알고리즘은 크게 Top-down 방식과 Bottom-up 방식이 있는데 이름에서도 유추 해 볼 수 있듯이
- Top-down은 큰 문제를 시작으로 이를 점점 작은 문제로 나누고 작은 문제를 해결해 문제를 푸는 방식
- Bottom-up은 작은 문제를 시작으로 결과를 이용해 점점 큰 문제를 해결해 나가는 방식
Top-down 방식
Top-down 방식은 재귀호출을 통해 문제를 나누어 제일 작은 문제를 해결하고 결과를 메모하여 그 값을 이용해 문제를 푸는 방식이다.
한번쯤은 봤을 메모이제이션을 이용한 피보나치수열 함수let memo = [0,1];
function fibo(n) {
if(typeof memo[n] !== 'number') {
memo[n] = fibo(n-1) + fibo(n-2);
}
return memo[n];
}Bottom-up 방식
Bottom-up 방식은 작은 문제를 해결하고 그값을 메모해 점점 큰문제로 나아간다. 보통 반복문을 이용해 구현하게 된다. 재귀 호출을 하지 않으므로 시간과 메모리의 사용량이 상대적으로 적다는 이점이 있다.
결국 두 방식 모두 메모를 통해 중복되는 연산을 하지않고 저장 된 값을 이용하는 것이다.여기서 DP알고리즘을 써야하는 조건을 알 수 있다.
DP 알고리즘을 사용하기 위한 조건
1) Overlapping Subproblems(겹치는 부분 문제)
- DP는 기본적으로 문제를 나누고 그 문제의 결과 값을 재활용해서 전체 답을 구한다. 그래서 동일한 작은 문제들이 반복하여 나타나는 경우에 사용이 가능하다.
2) Optimal Substructure(최적 부분 구조)
- 부분 문제의 최적 결과 값을 사용해 전체 문제의 최적 결과를 낼 수 있는 경우를 의미한다. 그래서 특정 문제의 정답은 문제의 크기에 상관없이 항상 동일하다.
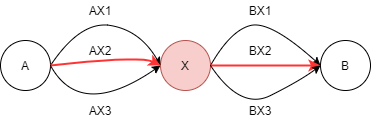
A에서 X로 가는 가장 빠른길이 AX2 이고 B에서 X로 가는 가장 빠른길이 BX2 라고 할 때,
A에서 B로 가는 가장 빠른길은 AX2-BX2 임을 알 수 있다.
이와 같이, 부분 문제에서 구한 최적 결과가 전체 문제에서도 동일하게 적용되어 결과가 변하지 않을 때 DP를 사용할 수 있게 된다.
DP 사용하기
일반적으로 DP를 사용하기 전에는 아래의 과정을 거쳐 진행할 수 있다.
1) DP로 풀 수 있는 문제인지 확인한다.
2) 문제의 변수 파악
3) 변수 간 관계식 만들기(점화식)
4) 메모하기
5) 기저 상태 파악하기
6) 구현하기
1. DP로 풀 수 있는 문제인지 확인
먼저 이 부분부터 매우 어렵다. 현재 직면한 문제가 작은 문제들로 이루어진 하나의 함수로 표현 될 수 있는지를 판단해야 한다.
보통 특정 데이터 내 최대화 / 최소화 계산을 하거나 특정 조건 내 데이터를 세야 한다거나 확률 등의 계산의 경우 DP로 풀 수 있는 경우가 많다.
2. 문제의 변수 파악
DP는 현재 변수에 따라 그 결과 값을 찾고 그것을 전달하여 재사용하는 것을 거친다. 즉, 문제 내 변수의 개수를 알아내야 한다.
예를 들어, 피보나치 수열에서는 n번째 숫자를 구하는 것이므로 n이 변수가 된다. 그 변수가 얼마인가에 따라 결과값이 다르지만 그 결과를 재사용하고 있다.
3. 변수 간 관계식 만들기
변수들에 의해 결과 값이 달라지지만 동일한 변수값인 경우 결과는 동일하다. 결과값을 그대로 이용할 것이기 때문에 그에따른 관계식을 만들어낼 수 있어야 한다.
그러한 식을 점화식이라고 부르며 그를 통해 코드 내에서 반복/재귀를 통해 문제가 자동으로 해결되도록 구축할 수 있게 된다.
예를 들어 피보나치 수열에서는 f(n) = f(n-1) + f(n-2) 였다.
4. 메모하기
변수 간 관계식까지 정상적으로 생성되었다면 변수의 값에 따른 결과를 저장해야 한다. 이것을 메모한다고 하여 Memoization이라고 부른다.
변수 값에 따른 결과를 저장할 배열 등을 미리 만들고 그 결과를 나올 때마다 배열 내에 저장하고 그 저장된 값을 재사용하는 방식으로 문제를 해결해 나간다.
이 결과 값을 저장할 때 보통 배열을 쓰며 변수의 개수에 따라 배열의 차원이 1~3차원 등 다양할 수 있다.
5. 기저 상태 파악하기
이제 가장 작은 문제의 상태를 알아야 한다. 보통 몇 가지 예시를 직접 테스트하여 구성하는 경우가 많다.
피보나치 수열을 예시로 들면, f(0) = 0, f(1) = 1과 같은 방식이다. 이후 두 가지 숫자를 더해가며 값을 구하지만 가장 작은 문제는 저 2개로 볼 수 있다.
해당 기저 문제에 대해 파악 후 미리 배열에 저장해두면 된다.
6. 구현하기
1) Bottom-Up - 반복문 사용
2) Top-Down - 재귀 사용