Convolution 연산과 다양한 차원에서의 연산방법을 소개합니다.
Convolution 연산의 역전파에 대해 설명합니다.
Convolution 연산은 오늘날 굉장히 많은 모델에서 이미지나 영상을 처리하기 위해 사용됩니다. 지금까지 배웠던 fully connected layer와 비교해서 CNN(Convolutional Neural Network)의 커널 연산이 가지는 장점과, Convolution 연산이 다양한 차원에서 어떻게 진행되는지를 이해하시고 넘어가시기 바랍니다.
Convolution 연산의 경우, 커널의 모든 입력데이터에 대해 공통으로 적용이 되기 때문에 역전파를 계산하는 경우에도 똑같이 Convolution 연산이 나오게 됩니다. 강의에서 그림과 함께 잘 설명되어 있기 때문에 커널을 통해 그레디언트가 어떻게 전달이 되는지, 역전파가 어떻게 이루어지는지 꼭 짚고 넘어가셨으면 좋겠습니다.
Convolution 연산 이해하기
다층신경망 MLP은 각 뉴런들이 선형모델과 활성함수로 모두 연결된 fully connnected 구조
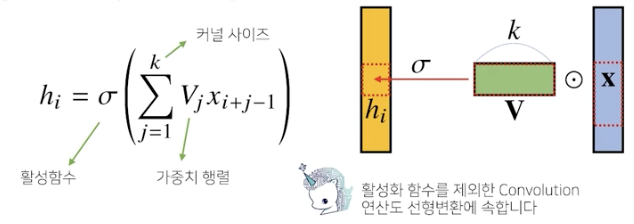
각 성분 hi에 대응하는 가중치 행 wi가 필요
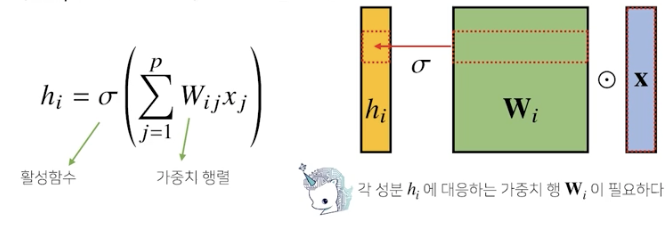
만일 i가 바뀌면 사용되는 가중치도 바뀜
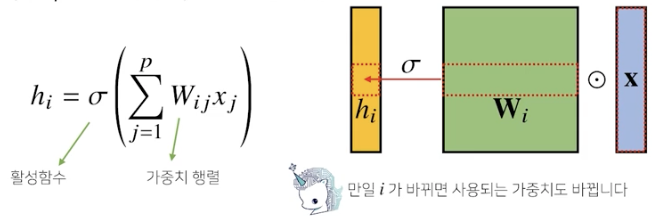
convolution 연산은 이와 달리 kernel (고정된 가중치 행렬) 을 입력벡터 상에서 움직여가면서 선형모델과 합성함수가 적용되는 구조
모든 i에 대해 적용되는 커널은 v로 같고 커널의 사이즈만큼 x상에서 이동하면서 적용
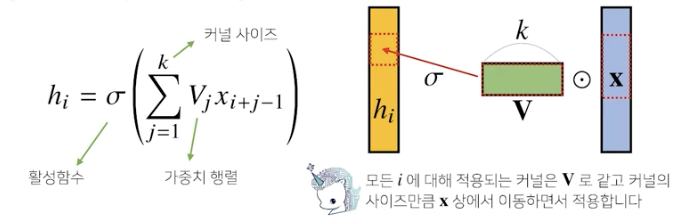
활성화 함수를 제외한 convolution 연산도 선형 변환에 속한다
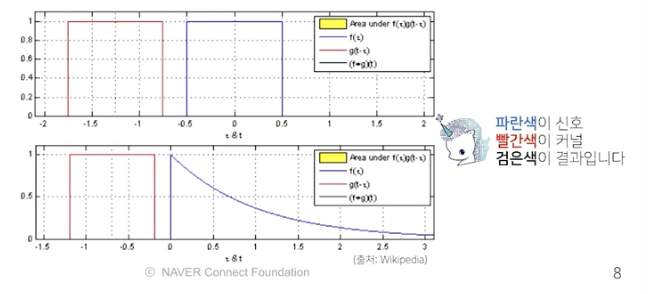
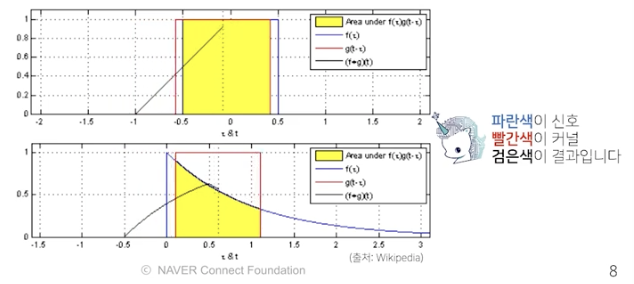
convolution 연산의 수학적인 의미는 신호 signal을 커널을 이용해 국소적으로 증폭 / 감소시켜 정보를 추출 / 필터링 하는 것

CNN에서 사용하는 연산은 사실 convolution이 아니고 cross-correlation이라 부른다

커널은 정의역 내에서 움직여도 변하지 않고 (translatoin invariant) 주어진 신호에 locally 국소적으로 적용함
다양한 차원에서의 convolution
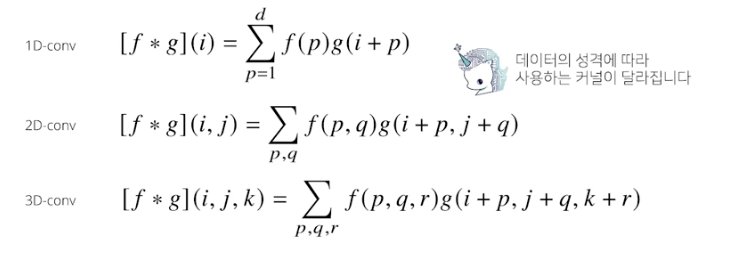
i, j, k가 바뀌어도 커널 f의 값은 바뀌지 않음

2차원 convolution 연산
2D-Conv 연산은 이와 달리 커널을 입력 벡터 상에서 움직여가면서 선형모델과 함성함수가 적용되는 구조
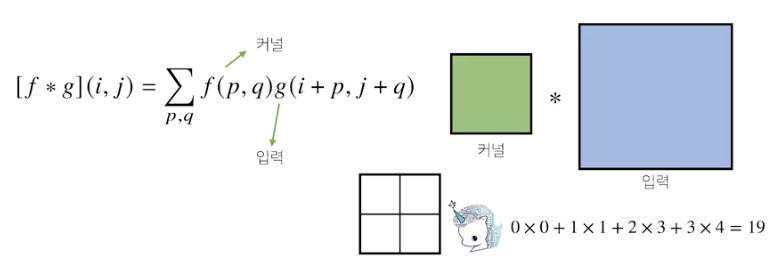
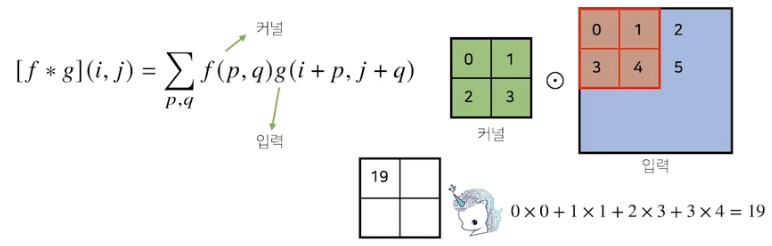
커널은 고정! 입력만 변하면서 연산
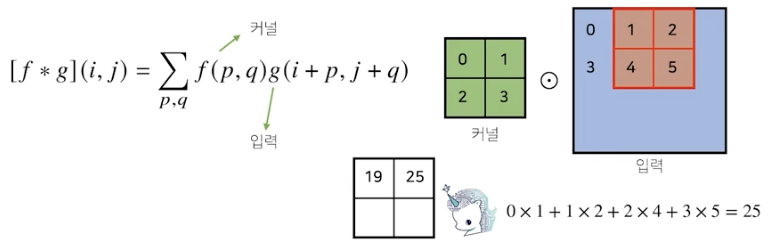
28 x 28 입력을 3 x 3 커널로 2D 연산을 하면 26 x 26이 된다

채널이 여러 개인 2차원 입력의 경우 2차원 convolution을 채널 개수만큼 적용
3차원부터는 행렬이 아닌 텐서!

채널이 여러개인 경우 커널의 개수와 채널 수와 입력의 채널 수가 같아야함
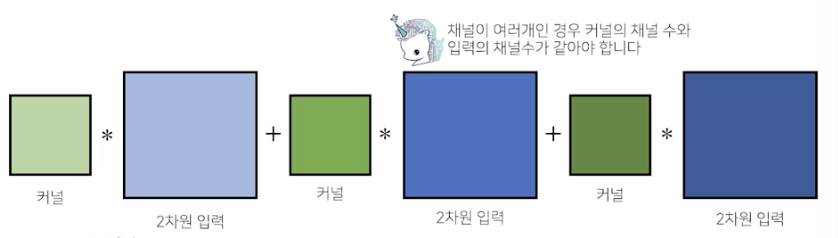
텐서를 직육면체 블록으로 이해해보자!
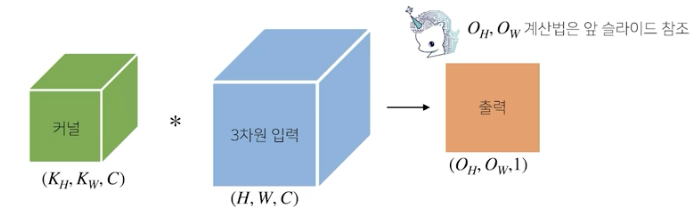
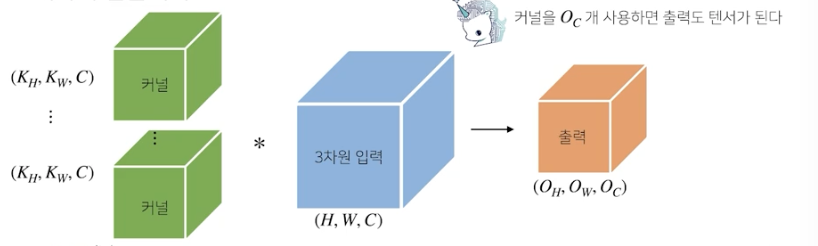
커널을 Oc개 사용하면 출력도 텐서가 됨
convolution 연산의 backpropagation
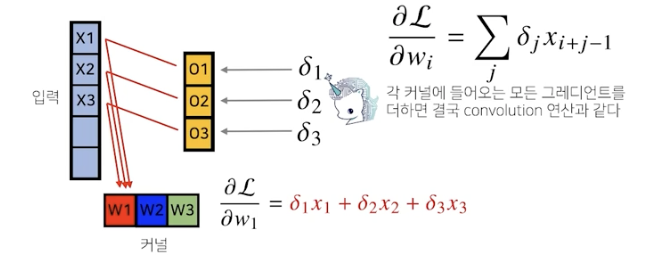
convolution 연산은 커널이 모든 입력 데이터에 공통으로 적용되기 때문에 역전파를 계산할 때도 convolution 연산이 나오게 됨

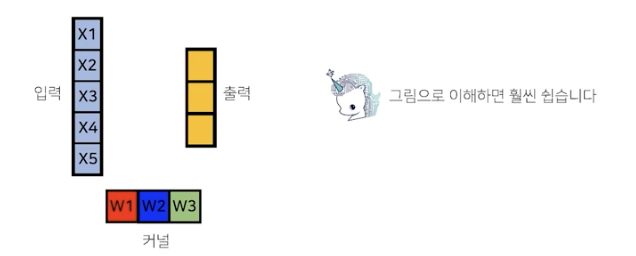
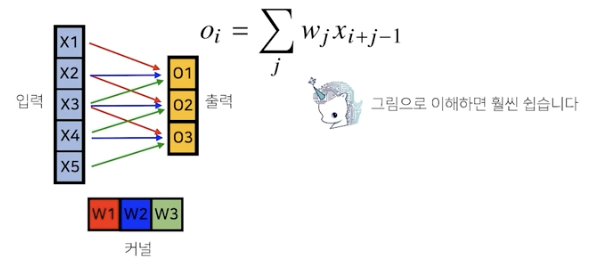
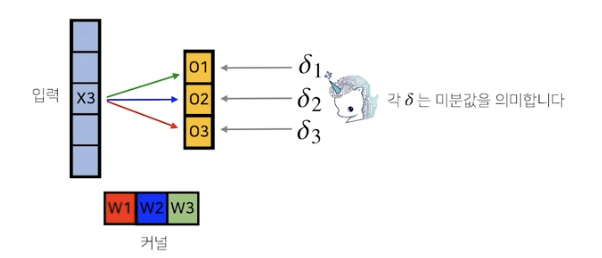
역전파 단계에서 다시 커널을 통해 gradient가 전달됨
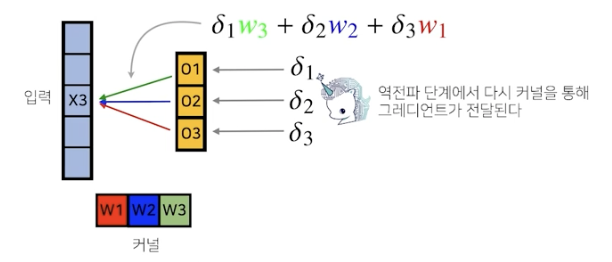

각 커널에 들어오는 모든 gradient를 더하면 결국 convolution 연산과 같다