조건부확률에서 이어지는 개념인 베이즈 정리와 인과관계 추론에 대해 설명합니다.
베이즈 정리는 데이터가 새로 추가되었을 때 정보를 업데이트하는 방식에 대한 기반이 되므로 오늘날 머신러닝에 사용되는 예측모형의 방법론으로 굉장히 많이 사용되는 개념입니다. 이 때 나오는 사전확률, 사후확률, evidence 등의 개념은 강의에서 나오는 예제를 활용해서 정확히 이해하시기 바랍니다.
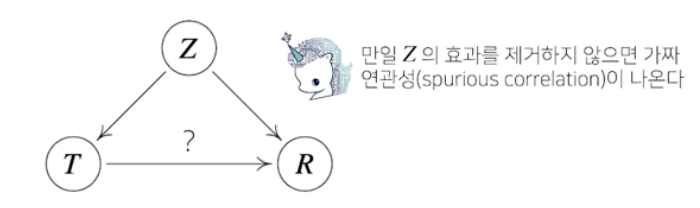
인과관계 추론의 경우, 조건부확률을 섣불리 사용해선 안되는 이유와 중첩효과를 제거함으로써 얻은 인과관계를 어떤 방식으로 활용할 수 있는지에 초점을 두고 공부하시면 좋겠습니다.
조건부 확률
베이즈 정리는 조건부확률을 이용하여 정보를 갱신하는 방법을 알려준다

조건부 확률 P(A|B)는 사건 B가 일어난 상황에서 사건 A가 발생할 확률을 의미

A라는 새로운 정보가 주어졌을 때 P(B)로 부터 P(B|A)를 계산하는 방법 제공
베이즈 정리: 예제



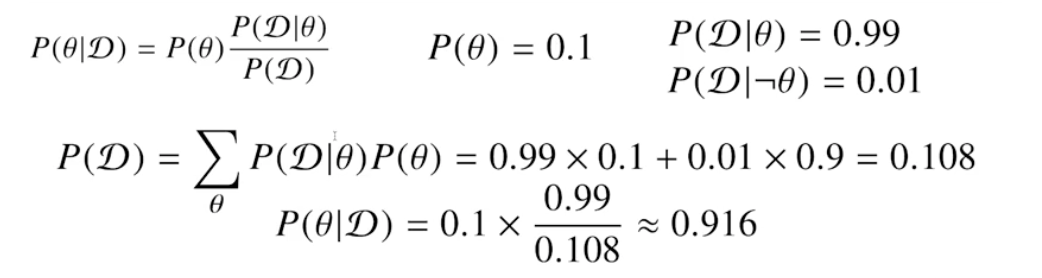
만일, 오검진될 확률(1종 오류)이 1%가 아닌 10%면 어떻게 되는가?
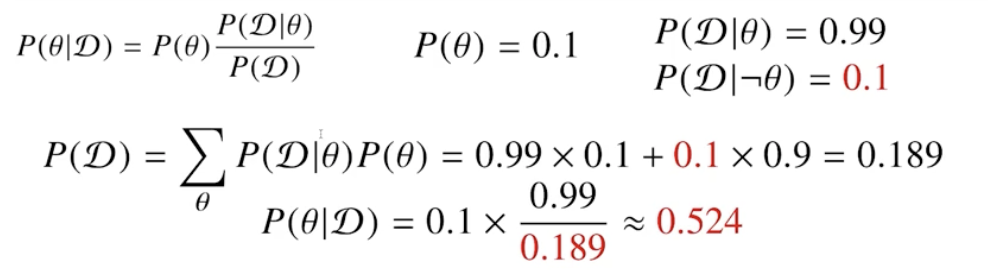
오탐율 false alarm이 오르면 테스트의 정밀도 precision이 떨어진다
조건부 확률 시각화
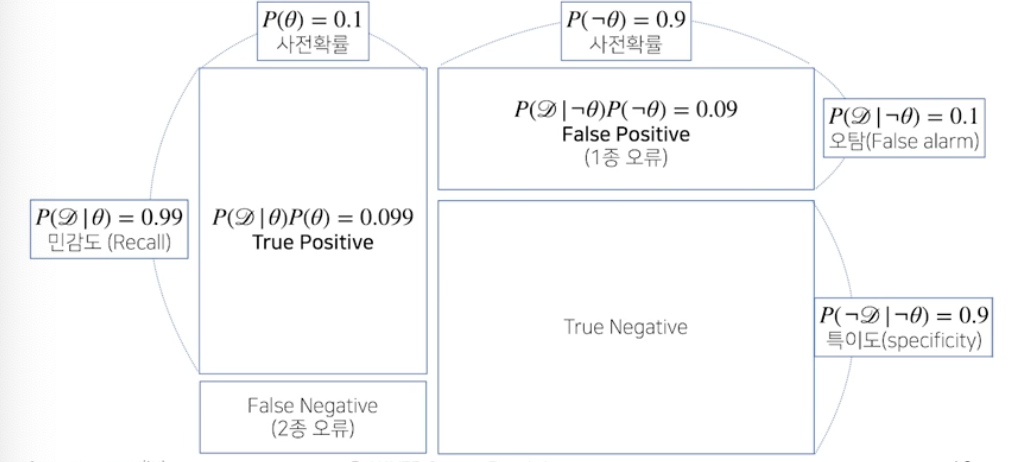
베이즈 정리를 통한 정보의 갱신
베이즈 정리를 통해 새로운 데이터가 들어왔을 때 앞서 계산한 사후확률을 사전확률로 사용하여 갱신된 사후확률을 계산할 수 있다


조건부 확률 -> 인과관계?
조건부 확률은 유용한 통계적 해석을 제공하지만 인과관계를 추론할 때는 함부로 사용 ㄴㄴ
데이터가 많아져도 조건부 확률만 가지고 인과관계를 추론하는 것은 불가능
인과관계는 데이터 분호의 변화에 강건한 예측모형을 만들 때 필요
단, 인과관계만으로는 높은 예측 정확도를 담보하기 어려움

인과관계를 알아내기 위해서는 중첩요인 confounding factor의 효과를 제거하고
원인에 해당하는 변수만의 인과관계를 계산해야 함