AI Math - Differentiation

미분의 개념과 그래디언트 벡터에 대해 설명합니다.
경사하강법의 알고리즘과 실제 코드에서의 구현을 보여줍니다.

접선의 기울기를 이용해서 함수의 최솟값으로 점을 이동시키는 원리를 알면 이를 바탕으로 경사하강법의 알고리즘과 수식을 이해할 수 있습니다.
특히 변수가 벡터인 경우, 편미분을 통해서 구한 그래디언트 벡터를 통해 d-차원으로 경사하강법을 확장할 수 있다는 개념을 확실하게 잡고 가시기 바랍니다.

미분

변수의 움직임에 따른 함수값의 변화를 측정하기 위한 도구로 최적화에서 제일 많이 사용하는 기법

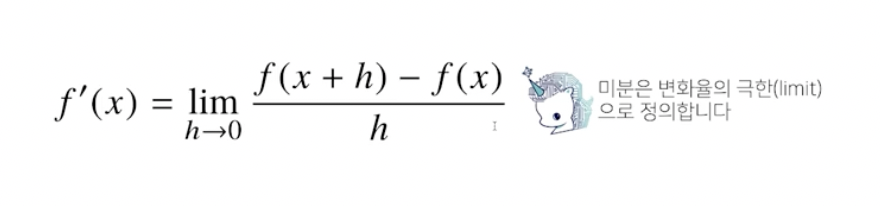
import sympy as sym
from sympy.abc import x

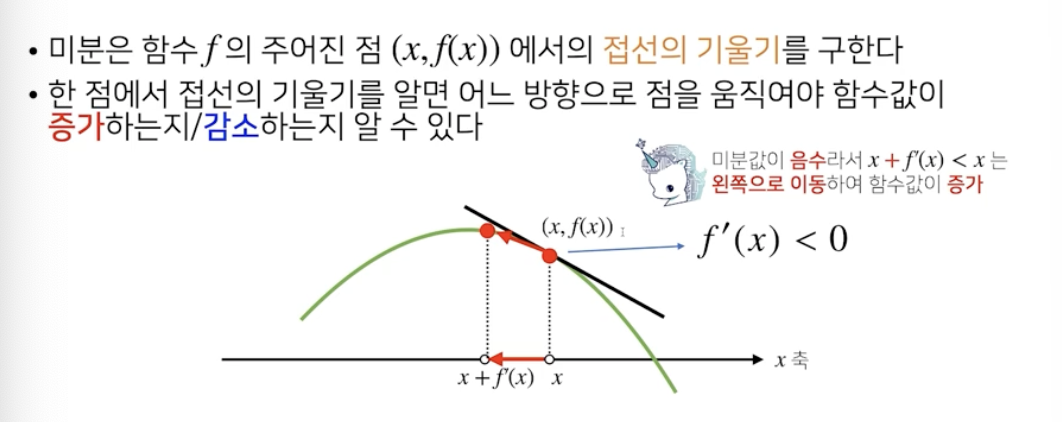
sym.diff(sym.poly(x**2 + 2*x +3), x)

Poly(2x+2,x,domain=Z)

함수 f의 주어진 점 (x, f(x))에서의 접선의 기울기를 구한다
접선의 기울기를 알면 어느 방향으로 점을 움직여야 함수값이 증가/감소하는지 알 수 있다

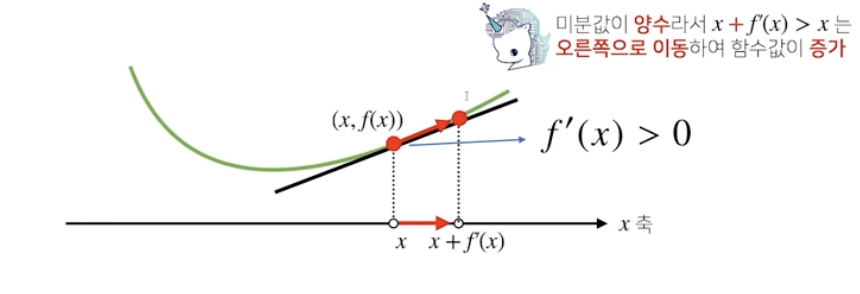
경사상승법 gradient ascent

미분값을 더하는 경우
함수의 극대값의 위치를 구할 때 사용

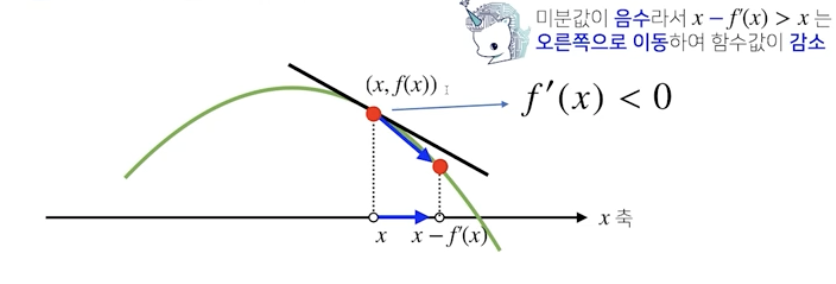
경사하강법 gradient descent

미분값을 빼는 경우
함수의 극소값의 위치를 구할 때 사용

경사상승/경사하강 방법은 극값에 도달하면 움직임을 멈춤

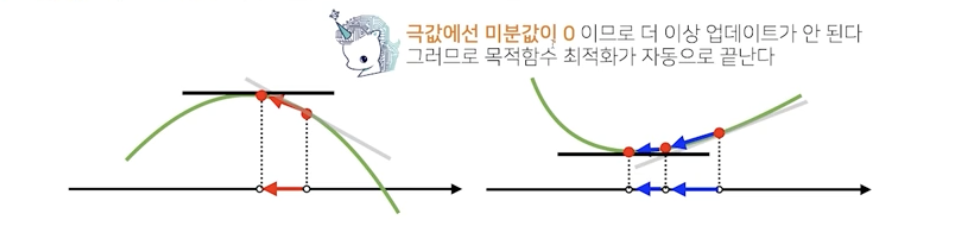
경사하강법:알고리즘

경사하강법으로 최소점 찾기

import numpy as np

def func(val):
  fun = sym.poly(x**2 + 2*x + 3)
  return fun.subs(x, val), fun

def func_gradient(fun, val):
  _, function = fun(val)
  diff = sym.diff(function, x)
  return diff.subs(x, val), diff

def gradient_descent(fun, init_point, lr_rate = 1e-2, epsilon = 1e-5):
  cnt = 0
  val = init_point
  diff, _ = func_gradient(fun, init_point)
  while np.abs(diff) > epsilon:
    val = val - lr_rate * diff
    diff, _ = func_gradient(fun, val)
    cnt += 1

  print("function: {}, num of operation : {}, minimum point : ({}, {})" .format(fun(val)[1], cnt, val, fun(val)[0]))

gradient_descent(fun=func, init_point = np.random.uniform(-2, 2))

function: Poly(x**2 + 2*x + 3, x, domain='ZZ'), 
num of operation : 551, 
minimum point : (-1.00000491250079, 2.00000000002413)

변수가 벡터인 경우

벡터가 입력인 다변수 함수의 경우 편미분 사용

import sympy as sym
from sympy.abc import x, y

sym.diff(sym.poly(x**2 + 2*x*y +3) + sym.cos(x + 2*y), x)

2x+2y−sin(x+2y)

각 변수별로 편미분을 계산한 gradient vector를 이용하여 경사하강/경사상승법에 사용 가능

What is a gradient vector?

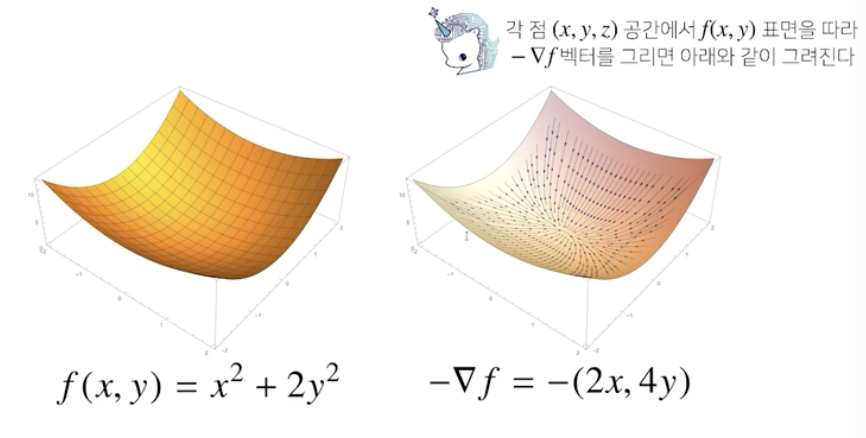
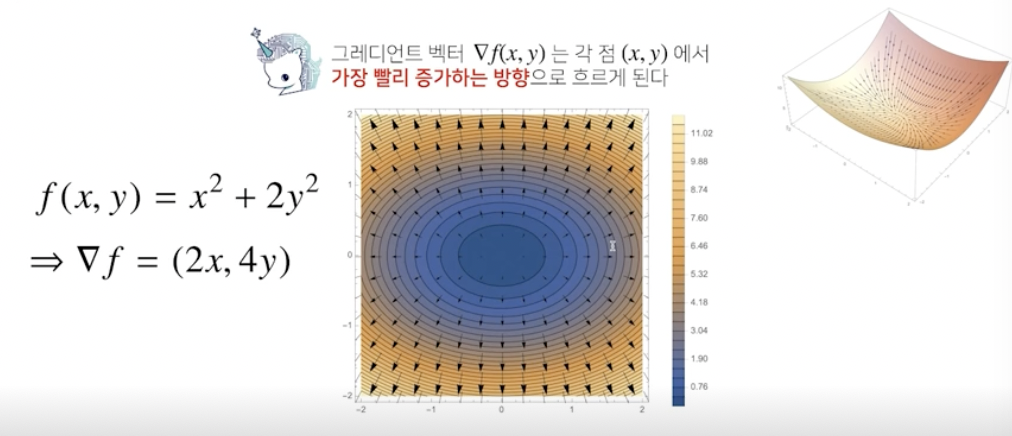
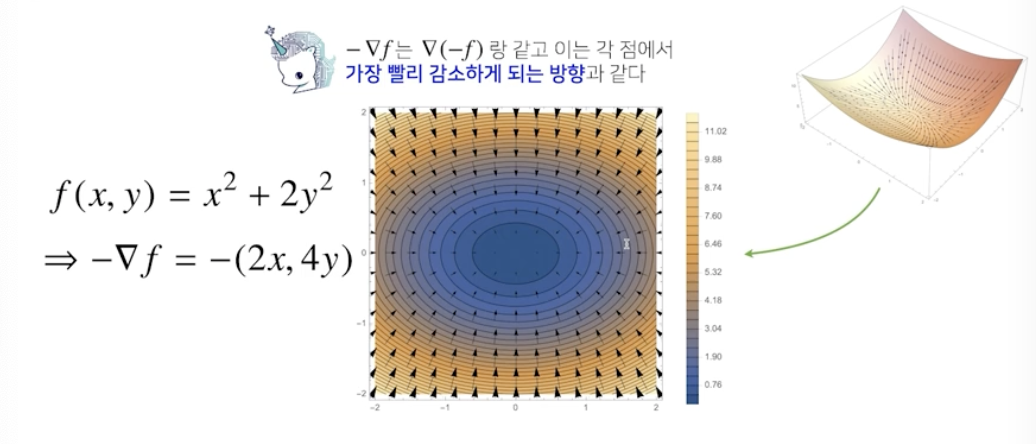
# multivariate Gradient Descent

import sympy as sym
from sympy.abc import x, y
import numpy as np

def eval_(fun, val):
  val_x, val_y = val
  fun_eval = fun.subs(x, val_x).subs(y, val_y)
  return fun_eval

def func_multi(val):
  x_, y_ = val
  func = sym.poly(x**2 + 2*y**2)
  return eval_(func, [x_, y_]), func

def func_gradient(fun, val):
  x_, y_ = val
  _, function = fun(val)
  diff_x = sym.diff(function, x)
  diff_y = sym.diff(function, y)
  grad_vec = np.array([eval_(diff_x, [x_, y_]), eval_(diff_y, [x_, y_])], dtype = float)

def gradient_descent(fun, init_point, lr_rate = 1e-2, epsilon = 1e-5):
  cnt = 0
  val = init_point
  diff, _ = func_gradient(fun, val)
  while np.lingalg.norm(diff) > epsilon:
    val = val - lr_rate * diff
    diff, _ = func_gradient(fun, val)
    cnt += 1

  print("function: {}, num of operation : {}, minimum point : ({}, {})" .format(fun(val)[1], cnt, val, fun(val)[0]))

pt = [np.random.uniform(-2, 2), np.random.uniform(-2, 2)]
gradient_descent(fun = func_multi, init_point = pt)