행렬의 개념과 연산, 그리고 벡터공간에서 가지는 의미를 설명합니다.
연립방정식 풀기와 선형회귀분석에 응용하는 방법을 소개합니다.
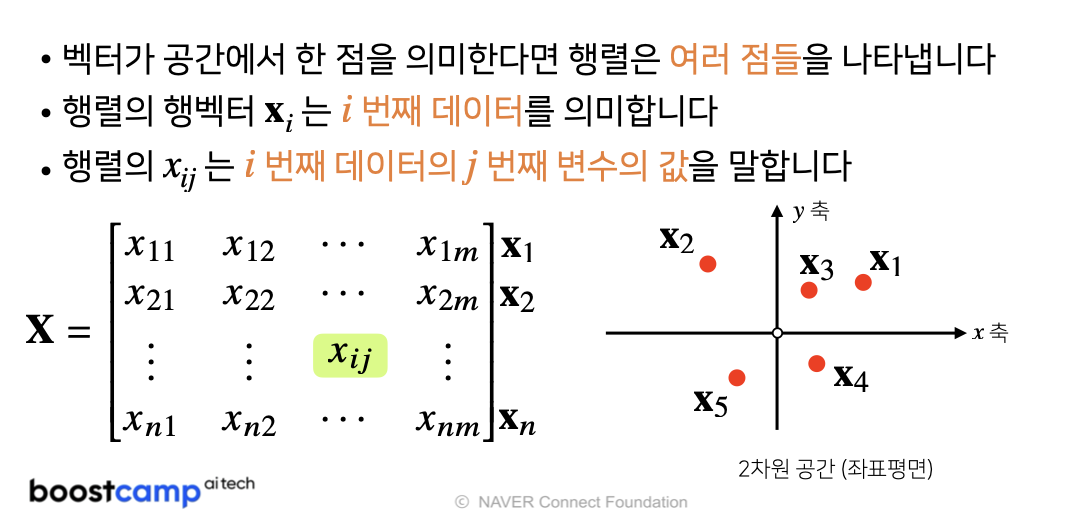
벡터의 확장된 개념인 행렬은 행(row)벡터를 원소로 가지는 2차원 배열로 벡터와 다르게 계산되는 연산들에 주의하셔야 합니다.
행렬연산은 딥러닝에서 가장 핵심적인 연산이라고 볼 수 있을만큼 중요하고, 자주 사용되기 때문에 행렬 연산의 메커니즘,그리고 이 때 가지는 기하학적 의미와 머신러닝에서 어떻게 사용되는지를 충분히 이해하고 넘어가시기 바랍니다.
행렬은 벡터를 원소로 가지는 2차원 배열
x = np.array([[1, -2, 3],
[7, 5, 0],
[-2, -1, 2]])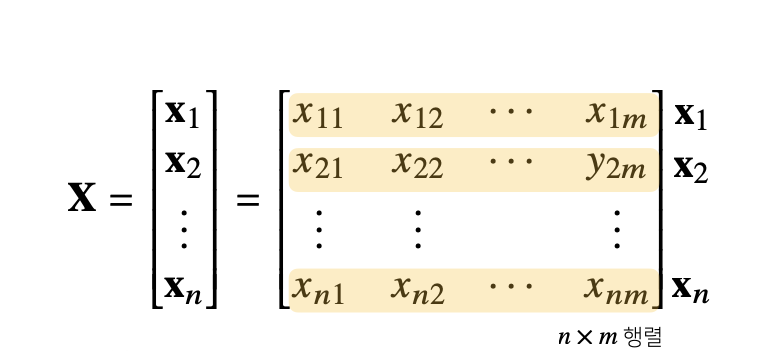
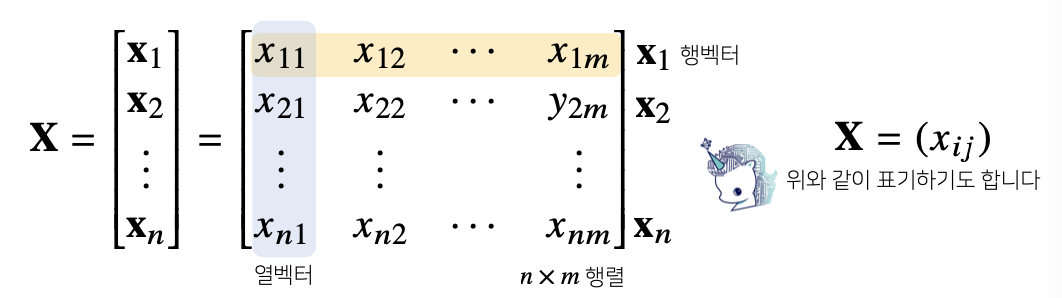
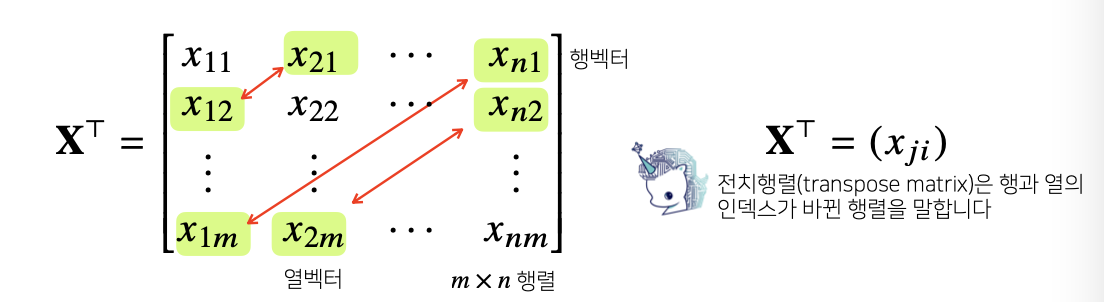
행렬은 행(row)과 열(column)이라는 인덱스(index)를 가짐
행렬의 특정 행(열)을 고정하면 행(열)벡터라 부름
행렬끼리 같은 모양을 가지면 덧셈, 뺄셈을 계산 가능
행렬 곱셈(matrix multiplication)은 i 번째 행벡터와 j 번째 열벡터 사 이의 내적을 성분으로 가지는 행렬을 계산
x = np.array([[1, -2, 3],
[7, 5, 0],
[-2, -1, 2]])
y = np.array([[0, 1],
[1, -1],
[-2, 1]])
# (0 + -2 + -6), (1 + 2 + 3)
x @ y
array([[-8, 6],
[ 5, 2],
[-5, 1]])
넘파이의 np.inner 는 i 번째 행벡터와 j 번째 행벡터 사이의 내적을 성분으로 가지는 행렬을 계산
x = np.array([[1, -2, 3],
[7, 5, 0],
[-2, -1, 2]])
y = np.array([[0, 1, -1],
[1, -1, 0]])
# 1 + -2 + -3
np.inner(x, y)
array([[-5, 3],
[ 5, 2],
[-3, -1]])행렬은 벡터공간에서 사용되는 연산자(operator)로 이해
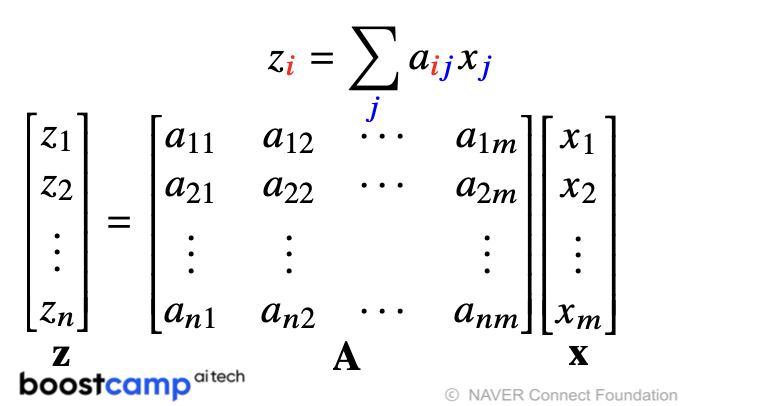
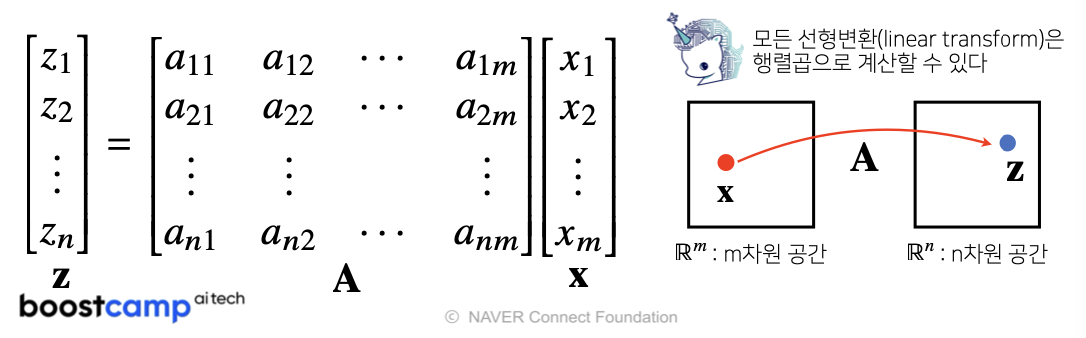
행렬곱을 통해 벡터를 다른 차원의 공간으로 보낼 수 있음
행렬곱을 통해 패턴을 추출할 수 있고 데이터를 압축할 수도
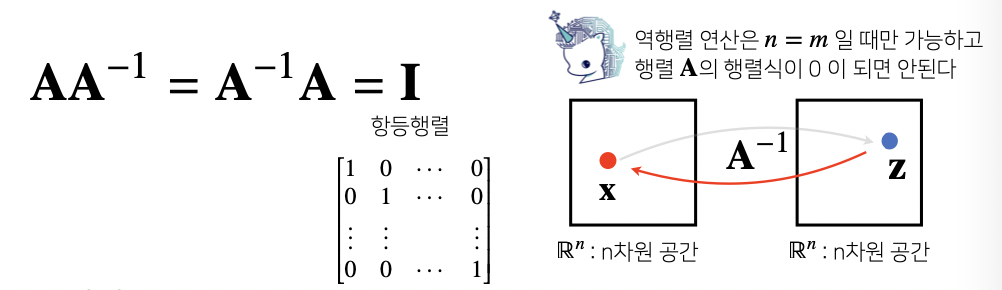
어떤 행렬 A 의 연산을 거꾸로 되돌리는 행렬을 역행렬(inverse matrix)이 라 부르고 A−1 라 표기
역행렬은 행과 열 숫자가 같고 행렬식
(determinant)이 0이 아닌 경우에만 계산
x = np.array([[1, -2, 3],
[7, 5, 0],
[-2, -1, 2]])
np.linalg.inv(x)
array([[ 0.21276596, 0.0212766 , -0.31914894],
[-0.29787234, 0.17021277, 0.44680851],
[ 0.06382979, 0.10638298, 0.40425532]])x @ np.linalg.inv(x)
array([[ 1.00000000e+00, -1.38777878e-17, 0.00000000e+00],
[-2.22044605e-16, 1.00000000e+00, -5.55111512e-17],
[-2.77555756e-17, 0.00000000e+00, 1.00000000e+00]])만일 역행렬을 계산할 수 없다면 유사역행렬(pseudo-inverse) 또는 무어-펜로즈(Moore-Penrose) 역행렬 A+ 을 이용

y = np.array([[0, 1],
[1, -1],
[-2, 1]])
np.linalg.pinv(y)
array([[ 5.00000000e-01, 4.09730229e-17, -5.00000000e-01],
[ 8.33333333e-01, -3.33333333e-01, -1.66666667e-01]])
np.linalg.pinv(y) @ y
array([[ 1.00000000e+00, -2.22044605e-16],
[ 5.55111512e-17, 1.00000000e+00]])