강의 소개
벡터의 기본 개념과 연산, 노름에 대해 소개합니다.
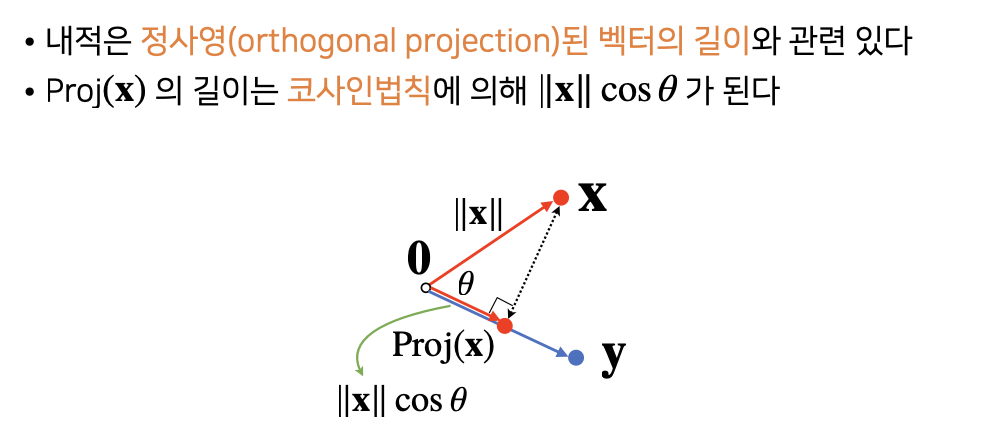
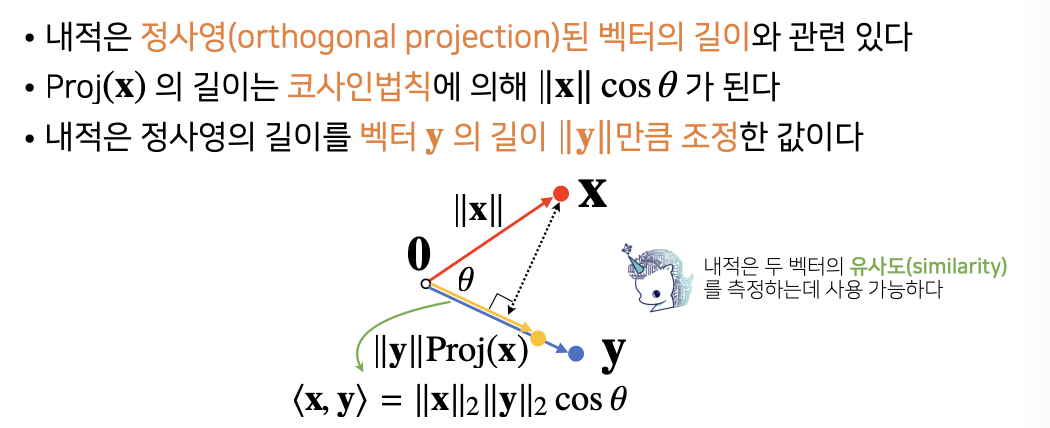
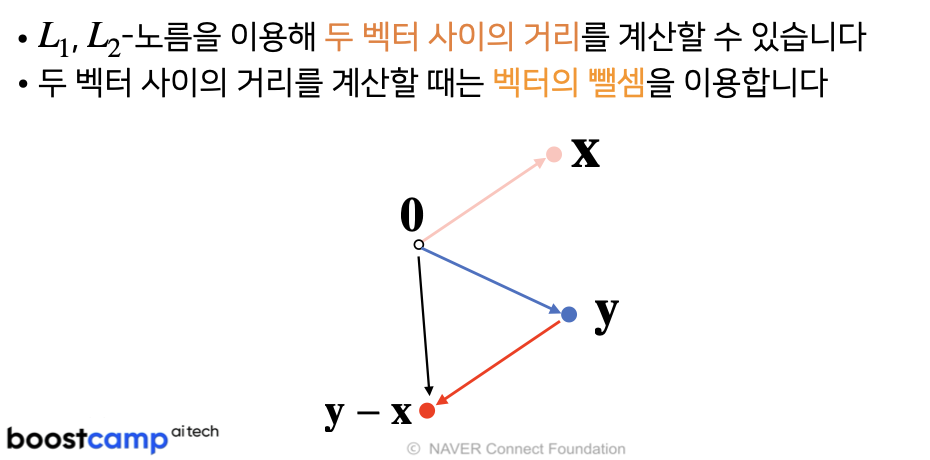
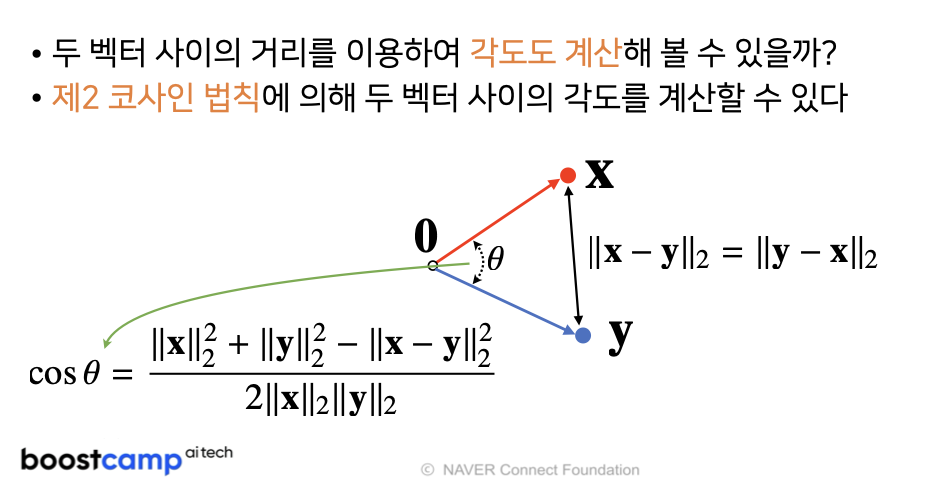
두 벡터 사이의 거리와 각도, 그리고 내적에 대해 설명합니다.
벡터는, 딥러닝에서 매우 중요한 선형대수학의 기본 단위가 되고, 앞으로 배우실 numpy에서도 굉장히 많이 사용되는 연산이기 때문에 확실하게 잡고 가셔야 할 개념입니다. 벡터간의 연산을 단순히 숫자 계산으로 끝내기보단, 공간에서 어떤 의미를 가지는지를 이해하는 것이 중요합니다.
노름이나 내적 같은 개념 또한, 그 자체로 가지는 기하학적인 성질과 이것이 실제 머신러닝에서 어떻게 사용되는지를 같이 생각해보시면서 공부하셨으면 좋겠습니다.
벡터는 숫자를 원소로 가지는 리스트(list) 또는 배열(array)
벡터는 공간에서 한 점
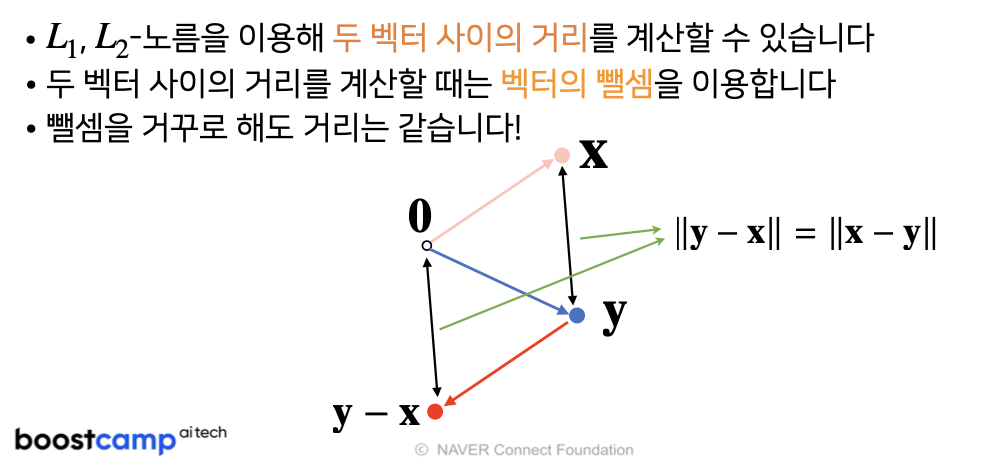
벡터는 원점으로부터 상대적 위치
벡터에 숫자를 곱해주면 길이만 변합니다
두 벡터의 덧셈은 다른 벡터로부터 상대적 위치이동을 표현합니다
norm
벡터의 노름(norm)은 원점에서부터의 거리
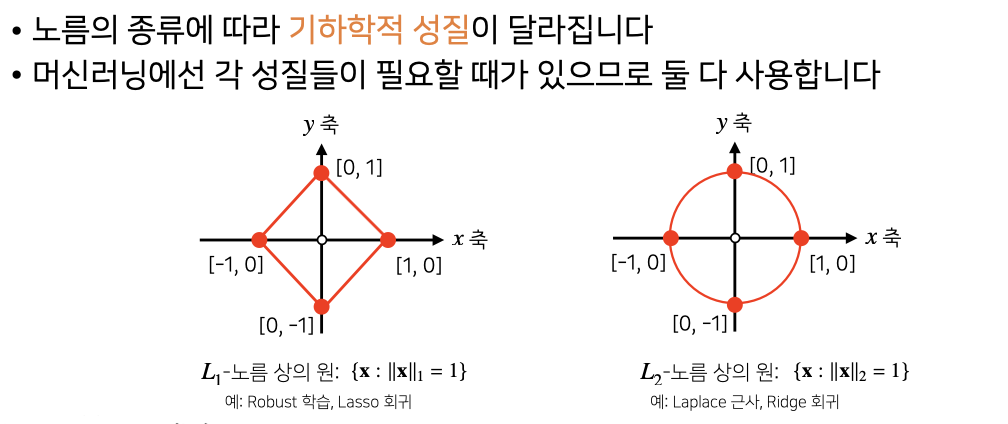
L1-노름은 각 성분의 변화량의 절대값을 모두 더합니다
L2-노름은 피타고라스 정리를 이용해 유클리드 거리를 계산
def l1_norm(x):
x_norm = np.abs(x)
x_norm = np.sum(x_norm)
return x_norm
def l2_norm(x):
x_norm = x*x
x_norm = np.sum(x_norm)
x_norm = np.sqrt(x_norm)
return x_norm노름의 종류에 따라 기하학적 성질이 달라집니다
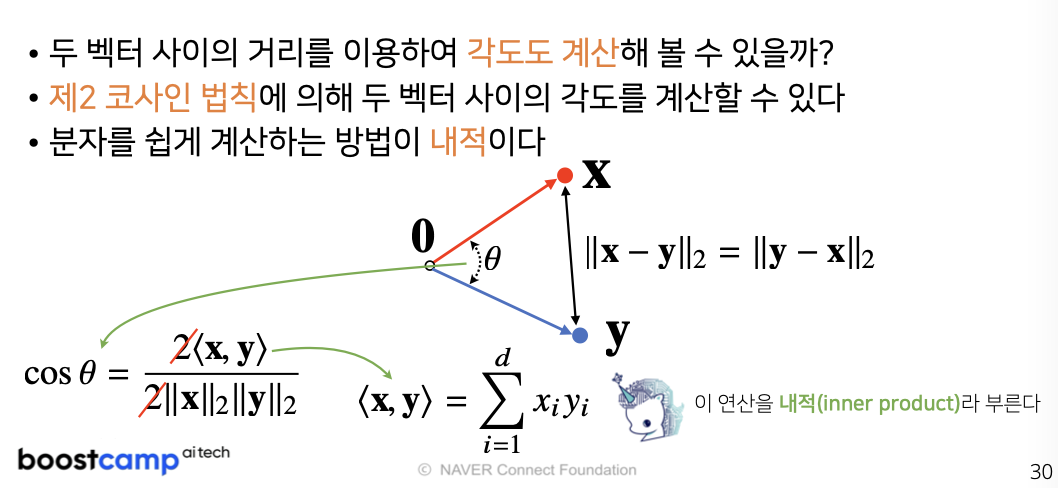
def angle(x, y):
v = np.inner(x, y) / (l2_norm(x)) * (l2_norm(y))
theta = np.arccos(v)
return theta