유한소수 판별하기

문제 설명
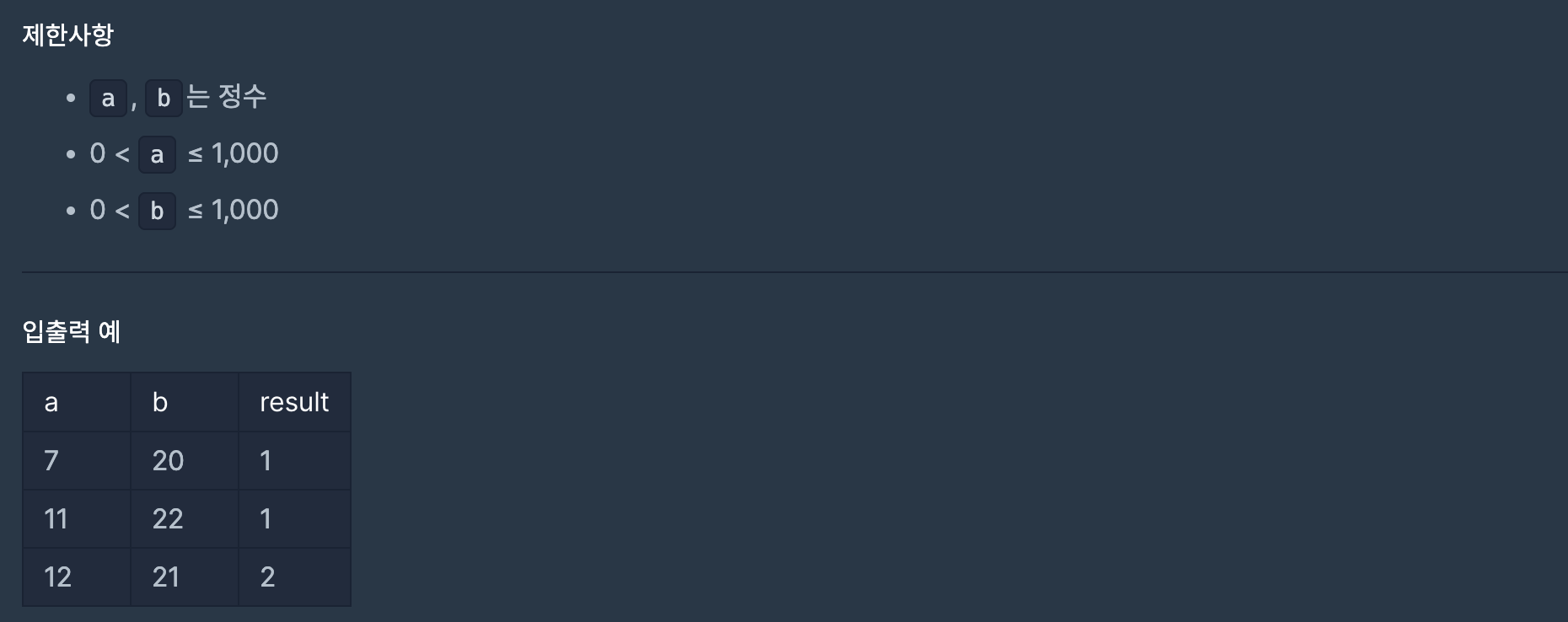
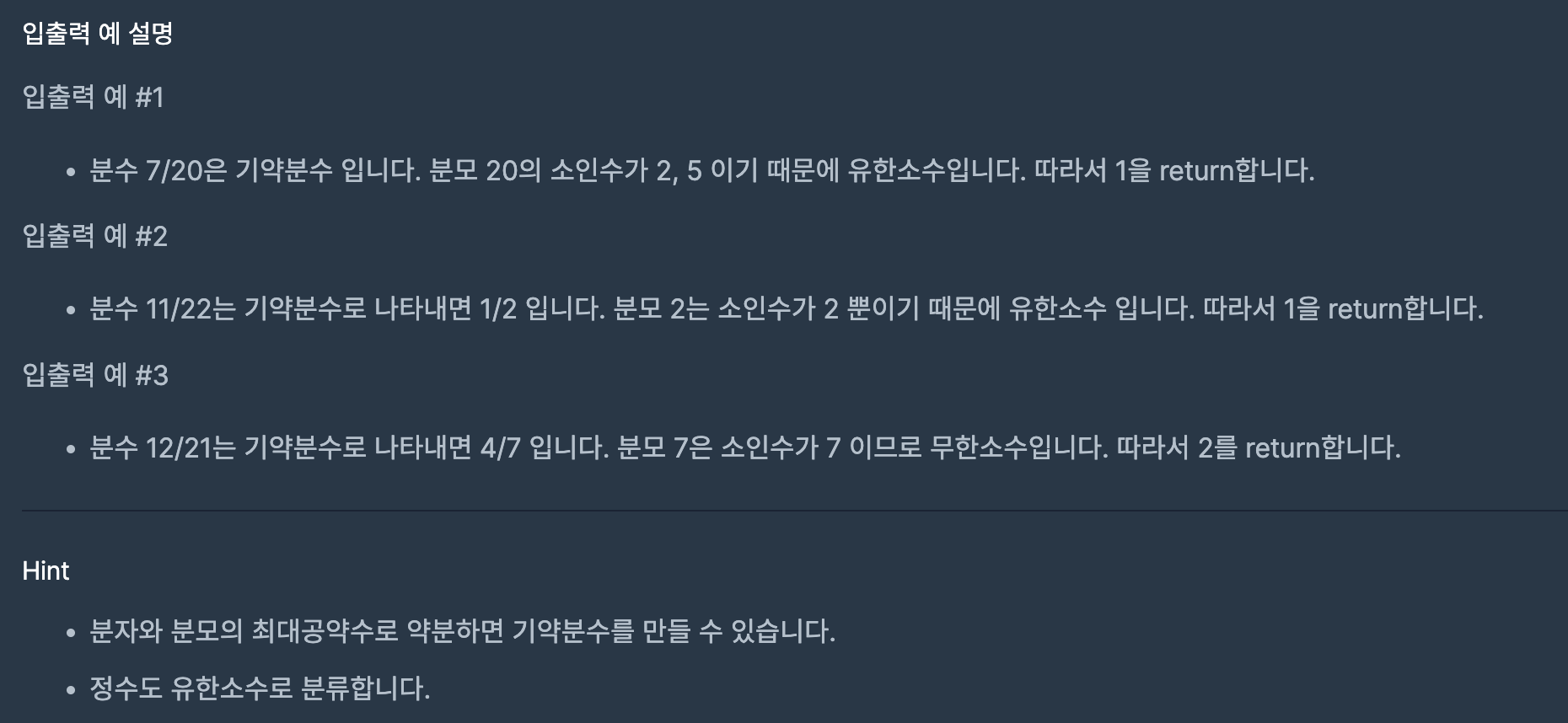
소수점 아래 숫자가 계속되지 않고 유한개인 소수를 유한소수라고 합니다. 분수를 소수로 고칠 때 유한소수로 나타낼 수 있는 분수인지 판별하려고 합니다. 유한소수가 되기 위한 분수의 조건은 다음과 같습니다.

• 기약분수로 나타내었을 때, 분모의 소인수가 2와 5만 존재해야 합니다.
  두 정수 a와 b가 매개변수로 주어질 때, a/b가 유한소수이면 1을, 무한소수라면 2를 return하도록 solution 함수를 완성해주세요.
  

나의 풀이

우선, 이 문제를 어떻게 한 단계씩 풀어나갈지 아래와 같이 생각했다.
1. 약분 되는지 판단하기 -> 최대 공약수를 구해야 함.
2. 기약분수로 나타내기 -> 분자, 분모를 최대 공약수로 나누어야 함. 이 문제에서는 분모만 나누면 됨
3. 분모의 소인수 구하기 -> 약분된 분모를 소인수분해 해야 함. 문제 설명에 있는 것처럼 2, 5라면 유한소수, 아니라면 무한소수 / 여기에서 주의할 점은 2와 5만 존재해야 한다.

// 최대 공약수 구하기
function cal_gcd(x, y) {
  return x % y === 0 ? y : cal_gcd(y, x % y)
}

// 소인수분해 하기
function primeFactors(n) {
  let result = [];
  let divisor = 2;
  
  while (n >= 2) {
    if (n % divisor === 0) {
      result.push(divisor)
      n = n / divisor;
    }
    
     else divisor ++;
    
  }
  
  return [...new Set(result)];
}


function solution(a, b) {
  const gcd = cal_gcd(a, b);
  a = a / gcd;
  b = b / gcd;
  
  const primes = primeFactors(b);
  return primes.find(n => n !== 2 && n !== 5) ? 2 : 1
  
}

다시 보니 굉장히 길게 썼다...
소인수분해 코드는 전에 프로그래머스 문제를 풀면서 작성해둔 내 포스트를 슬쩍 보고... 작성했고, 최대공약수 구하는 것은 점점 외워가고 있어서 혼자 작성한 뒤 슬쩍 내 포스트를 뒤져 확인했었다.

마지막 줄에 return primes.find(n => n !== 2 && n !== 5) ? 2 : 1 부분에서 굉장히 고민했었다. 2와 5만 들어있는 것을 찾아내야 하는데, 그걸 어떻게 쓸까 하다가 find 메서드와 삼항연산자를 활용하였다. 배열 안에 들어있는 요소가 2와 5이 아닐 경우 참을 반환하도록 하였고, 이를 위의 코드와 같이 적었다.

다른 사람의 풀이

function solution(a, b) {
    return Number((a/b).toFixed(10)) == a/b ? 1 : 2
}

toFixed 메서드를 처음으로 접했다.

MDN을 찾아보고 console에 직접 찍어보니 아래와 같이 나왔다.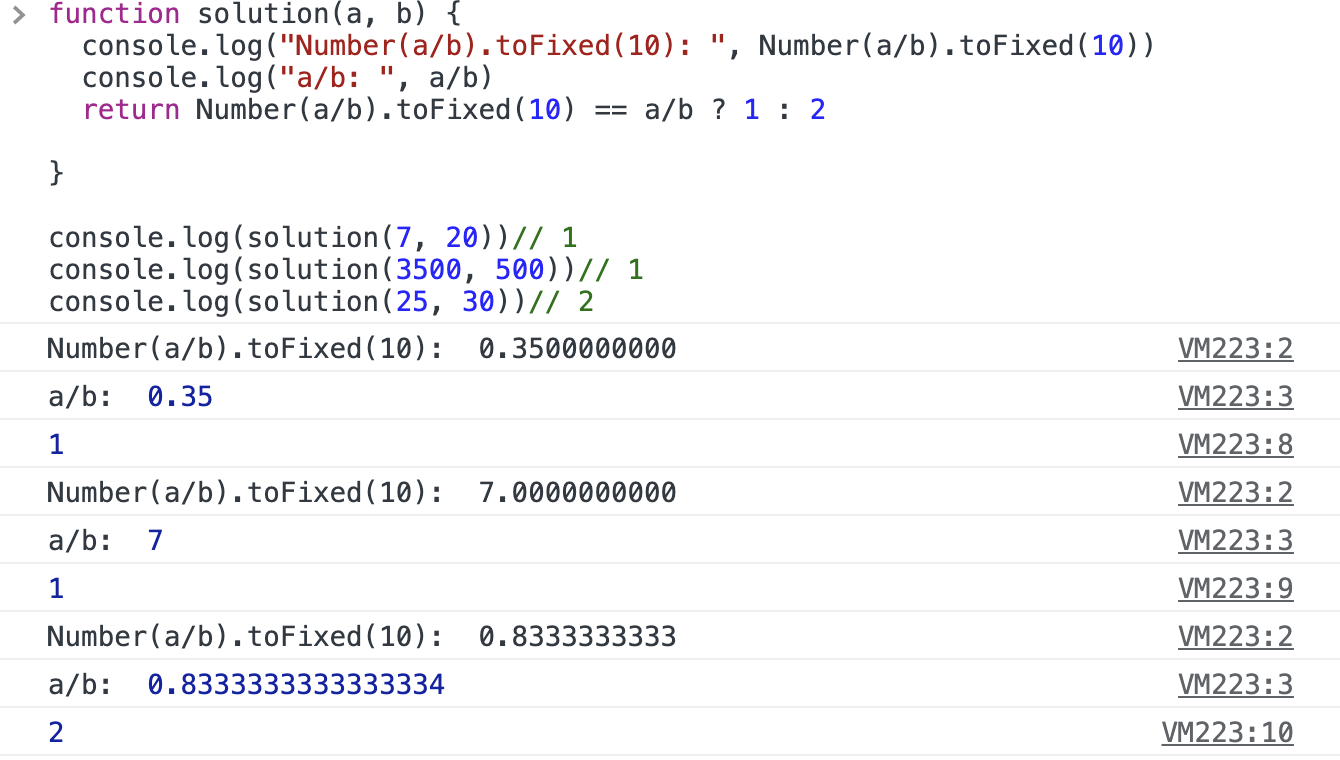

유한소수는 말 그대로 한계가 있는 소수이고, 무한소수는 끝없이 계속되기 때문에 이러한 방법으로 비교하여 반환하는 것도 좋은 방법이라 생각한다.