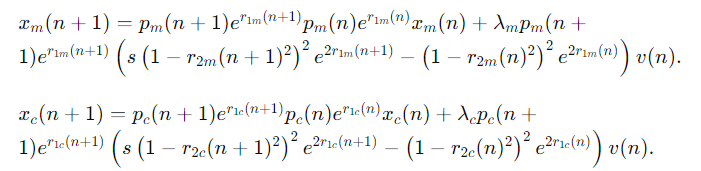
Abstarct

이 작업은 고장 진단과 예지 정비를 위한 새로운 데이터 중심 솔루션을 제시합니다. 이 솔루션은 비정상적인 다변량 시계열 데이터에 적합한 데이터 증강 방법을 포함합니다. 시간에 따라 변하는 자기회귀 과정을 기반으로 한 이 방법은 제한된 샘플 수에서 핵심 정보를 추출하고, 진단 및 예지 솔루션 개발에 유리하게 새로운 인공 샘플을 생성할 수 있습니다. 제안된 접근 방식은 세 개의 실세계 데이터셋을 바탕으로 고장 진단 문제에 대해 테스트되었으며, 두 종류의 기계 학습 방법을 사용했습니다. 결과는 제안된 방법이 모든 테스트 케이스에서 성능을 향상시킴을 나타냅니다.

1. INTRODUCTION

이 연구는 장비와 시스템의 고장 진단 및 예지 정비, 즉 PHM(Prognostics and Health Management) 또는 예측 유지보수 등에 대한 최근 수십 년 동안의 활발한 조사와 실세계 솔루션 개발에 중점을 둔 것입니다. 고장 발생을 피하거나 그 영향을 줄이는 것은 다운타임 감소, 생산량 및 안전성 향상과 같은 혜택으로 이어지기 때문에 이에 대한 동기는 분명합니다. 다양한 방법이 제안되어 왔으며, 이는 인구 통계에 기반한 신뢰성 방법부터 최첨단 머신러닝 방법을 사용하는 데이터 기반 솔루션, 고급 고장 메커니즘 모델을 포함하는 물리 기반 접근 방식에 이르기까지 다양합니다. 그러나 PHM 솔루션의 성공적인 개발과 적용을 제한하는 가장 중요한 요소는 방법 자체에 있는 것이 아니라, 해당 솔루션의 개발과 검증에 사용될 수 있는 좋은 품질의 역사적 데이터의 가용성과 관련된 일반적인 제한에 있습니다.

이 연구는 다변량 시계열 데이터의 증강을 위한 새로운 방법을 제안하며, 이는 시간 변화 자기회귀(TVAR) 모델을 기반으로 합니다. 목표는 부족한 데이터에서 정보를 추출하고 이를 사용하여 진단 및 예지 솔루션의 품질을 향상시킬 수 있는 추가 샘플을 생성하는 것입니다. 특히 비정상 시계열을 직접 처리할 수 있다는 점에서 고장 진단 및 예지 문제에 특히 적합합니다. 이 논문은 TVAR에 관련된 기술적 배경, TVAR을 이용한 데이터 증강의 제안된 적용, 실험 및 결과의 설명과 논의, 그리고 결론으로 구성되어 있습니다.

2. BACKGROUND ELEMENTS

2.1. Considerations About The Time Series Data

이 논문은 센서 시계열 데이터를 시계열 그룹 또는 클래스의 관점에서 증강하는 문제를 다룹니다. 이를 위해 분석될 데이터를 "이상"과 "정상"과 같은 클래스로 나눈다고 가정합니다. 또한, 제안된 방법으로 증강될 시계열 데이터셋에 대해 다음과 같은 가정을 고려합니다:
A1) 같은 데이터셋의 시계열은 동일하게 샘플링됩니다.
A2) 같은 클래스의 시계열은 동일한 다변량, 잠재적으로 비정상적인 확률 과정으로 모델링될 수 있습니다.
잠재적 비정상 행동은 확률 과정의 속성이 시간에 따라 변할 수 있음을 의미합니다.
제안된 데이터 증강은 가정 A2)에서 유래하며, 주어진 클래스의 시계열을 모델링하기 위한 적절한 확률 과정을 찾은 다음, 이를 사용하여 확률 과정의 새로운 실현으로 새 시계열을 생성하는 것으로 구성됩니다.

2.2. . Considerations About The Time Series Models

이 작업에서는 시그널 클래스를 특징짓는 확률 과정을 나타내기 위해 파라메트릭 시계열 모델을 사용합니다. 이러한 모델은 시계열의 샘플과 확률적 순간이 시간에 따라 어떻게 변하는지 수학적으로 설명합니다. 잘 알려진 모델 예로는 자기회귀(AR), 자기회귀 이동평균(ARMA), 자기회귀 통합 이동평균(ARIMA)이 있습니다. 이러한 모델은 종종 데이터가 정상 상태이거나 데이터의 잠재적 비정상성이 특정 형태(예: 추세 및 계절성)를 따를 것을 요구하여, 데이터에서 뺄셈, 차분 또는 기타 변환을 통해 추출될 수 있습니다. 그러나 실제 시계열은 종종 전통적 접근법으로는 모델링할 수 없는 다양한 비정상 행동을 보입니다.

전통적 접근법과 달리, 시간 변화 자기회귀(TVAR) 모델은 데이터의 비정상성을 더 잘 포착하기 위해 시간에 따라 그 매개변수가 변할 수 있도록 합니다. 이 변화는 TVAR 기저 함수, 가중치, 모델 순서의 집합에 의해 제어됩니다. 이런 양들이 어떻게 선택되는지에 따라 다양한 비정상 행동을 모델링할 수 있습니다. 이러한 강력한 모델링 능력 덕분에, 우리는 시계열의 기본 확률 과정을 TVAR 모델로 특징짓기로 결정하였고, 이는 같은 클래스에 속하는 시계열이 같은 TVAR 표현을 공유할 것을 의미합니다. 다양한 비정상 데이터(예: 음향 신호, 뇌전도(EEG), 레이더 클러터 데이터)를 모델링하기 위해 TVAR 기저 함수와 매개변수에 대한 다양한 맞춤 설정이 제안되었습니다. 여기서, 우리는 (de Souza, Kuhn, & Seara, 2019)에서 제안된 맞춤 설정을 선택하고 이를 데이터 증강 절차를 도출하기 위한 시작점으로 사용합니다.

2.3. TVAR Model

VAR 모델은 매개변수가 시간에 따라 변함으로써 데이터의 비정상성을 더 잘 포착할 수 있습니다. 특히, (de Souza, Kuhn, & Seara, 2019)에서 제안된 맞춤 설정을 통해, 평균과 공분산이 사용자가 미리 정한 함수 형태로 서로 다른 비율로 수렴하도록 할 수 있습니다. 이 맞춤 설정은 TVAR 기저 함수의 특정 표현식을 선택함으로써 얻어집니다.

이 연구는 TVAR 모델을 사용하여 평균 벡터와 공분산 행렬의 비정상 행동을 모델링하고, 이를 통해 데이터 증강 방법을 제안합니다. 주요 초점은 TVAR 보간 함수 p(n)을 얻는 것입니다.

3. DATA AUGMENTATION WITH TVA

두 TVAR 하위 모델 사용: 평균과 공분산이 시간에 따라 서로 다른 형태로 변화하는 시계열을 모델링하기 위해, 평균을 위한 TVARm 모델과 공분산을 위한 TVARc 모델, 두 개의 TVAR 하위 모델을 사용합니다. 각 하위 모델은 자체 보간 함수
p m(n)과 p c(n) 및 매개변수 집합을 가집니다.

경험적 통계 계산: 데이터에서 일차 및 이차 경험적 통계를 계산하여 이를 기반으로 보간 함수 p m(n)과 pc(n)을 적합시킵니다. 이 과정은 앙상블 평균을 사용하여 수행됩니다.

보간 함수 찾기: 단변량 시계열 데이터셋을 예로 들어 보간 함수를 찾는 방법을 제시하며, 이 방법은 다변량 경우로 확장될 수 있습니다. 보간 함수 pm(n)은 평균 m(n)에, pc(n)은 공분산 c(n)에 대해 각각 보간됩니다.

사인파 회귀를 통한 보간: 많은 PHM 시계열이 진동하는 특성을 가지고 있으므로, 사인파 모델을 사용한 보간을 제안합니다. 이는 이산 푸리에 변환(DFT)을 기반으로 하는 사인파 회귀를 통해 수행됩니다. 가장 중요한 주파수를 포함하는 사인파 회귀 공식을 통해
pm(n)과 pc(n)을 얻습니다.

데이터 증강 절차: 제안된 데이터 증강 절차는 증강된(새로운 합성) 시계열 데이터를 생성하기 위해 위에서 얻은 보간 함수와 매개변수를 사용합니다. 이 과정은 모든 클래스에 대해 반복될 수 있으며, 이상 감지와 같은 특정 문제에 대한 데이터 증강의 효과를 평가하기 위해 설계되었습니다.

이 접근 방법은 비정상 시계열 데이터를 효과적으로 다루며, 평균과 공분산이 시간에 따라 변화하는 복잡한 시계열 데이터의 특성을 포착하고 모델링할 수 있는 새로운 방법을 제공합니다. 데이터 증강을 통해 제한된 데이터로부터 더 많은 정보를 추출하고, 기계 학습 모델의 학습과 일반화 능력을 개선하는 것이 목적입니다.

4. EXPERIMENTAL STUDY

4.1. Datasets

이 연구에서는 세 가지 공개 단변량 시계열 데이터셋을 이상 탐지 연구에 사용하였습니다:

CWRU 데이터셋: 케이스 웨스턴 리저브 대학교에서 제공한 베어링 진동 신호로 구성되어 있습니다. 이 데이터는 전기 모터의 구동단 베어링에서 측정된 진동 신호를 포함하며, 다양한 부하 하에서 운영되었습니다.
PHMDC2019 데이터셋: 2019년 예지 건강 관리 데이터 챌린지에서 제공된 알루미늄 랩 조인트의 피로 실험에서 측정된 램 웨이브를 포함합니다. 이 데이터셋은 T1에서 T8까지의 8개 시료에 대해 다양한 하중이 적용되었으며, 각 시료에 대해 크랙 길이가 측정되었습니다. 관측된 크랙 길이가 4mm를 초과하는 경우 해당 샘플을 "손상" 클래스로 간주하였습니다.
Ford A 데이터셋: 자동차 엔진에서 측정된 소음 신호로 구성되어 있으며, 정상 또는 고장 증상을 나타내는 엔진에서 측정된 신호를 포함합니다. 이 데이터셋은 이상 탐지를 위한 신호 모음으로, Ford 분류 챌린지의 일부로 처음 제안되었습니다.

4.2. 기계 학습 모델

데이터 증강 방법은 이상 탐지를 위한 시계열 분류 문제에서 두 가지 기계 학습 모델, 즉 컨볼루션 신경망(CNN)과 랜덤 포레스트(RF)를 사용하여 평가되었습니다. CNN 아키텍처는 시계열 분류를 위한 Tensorflow/Keras 튜토리얼에서 제공되며, RF 모델은 Python의 scikit-learn 라이브러리를 사용하여 구현되었습니다. RF 모델은 시계열 데이터에서 추출된 탭울러 특성 표현에 적합하도록 설계되었습니다.

4.3. 데이터 증강 절차

제안된 데이터 증강 방법(TvarAug)은 TSAug 라이브러리에 의해 제공되는 전형적인 시계열 변환과 비교되었습니다. TSAug는 백색 가우시안 노이즈 추가, 데이터 포인트의 무작위 삭제 및 0으로 채우기, 데이터 포인트의 무작위 이동, 일부 데이터 포인트의 시간 해상도 감소 등 다양한 변환을 시뮬레이션합니다. 제안된 증강 방법은 여러 파라미터 값을 사용하여 TVARm 및 TVARc 표현식을 생성하고, 원본 시계열 데이터의 동적 패턴을 포착하면서 새로운 합성 신호 세그먼트를 생성하는 데 필요한 확률성을 도입합니다.
이 요약은 각 문단의 주요 내용을 간략하게 설명합니다. 데이터셋 섹션은 사용된 세 가지 데이터셋의 출처와 특성에 대해 설명하고, 기계 학습 모델 섹션은 실험에 사용된 두 가지 모델(CNN과 RF)에 대해 설명합니다. 마지막으로, 데이터 증강 절차 섹션은 제안된 증강 방법과 기존의 TSAug 라이브러리를 사용한 방법을 비교하여 설명합니다.