Abstract

Contrastive learning은 셀프-슈퍼바이즈드 방식으로 시계열 데이터에서 표현을 학습하는 데 효과적이라는 것이 입증되었습니다. 그러나 유사한 시계열 인스턴스나 시계열 내 인접한 타임스탬프의 값을 대조하면 이들의 고유한 상관 관계를 무시하게 되어 학습된 표현의 품질이 저하됩니다. 이 문제를 해결하기 위해 우리는 시계열에 대한 간단하지만 효과적인 소프트 대조 학습 전략인 SoftCLT를 제안합니다. 이는 0에서 1 사이의 소프트 할당을 도입한 인스턴스별 및 시간적 대조 손실을 통해 달성됩니다. 구체적으로, 데이터 공간에서 시계열 간의 거리로 정의된 인스턴스별 대조 손실과 타임스탬프의 차이로 정의된 시간적 대조 손실에 대한 소프트 할당을 정의합니다. SoftCLT는 시계열 대조 학습을 위한 플러그 앤 플레이 방식으로, 복잡한 추가 작업 없이 학습된 표현의 품질을 향상시킵니다. 실험에서 우리는 SoftCLT가 분류, 반-지도 학습, 전이 학습 및 이상 탐지 등 다양한 다운스트림 작업에서 일관되게 성능을 향상시키며 최첨단 성능을 보여준다는 것을 입증합니다. 코드는 이 저장소에서 이용할 수 있습니다: https://github.com/seunghan96/softclt.

1.INTRODUCTION

시계열 (TS) 데이터는 금융, 에너지, 헬스케어, 교통 등 많은 분야에서 널리 사용됩니다. 그러나 TS 데이터를 주석하는 것은 상당한 도메인 전문 지식과 시간이 필요하여 어려움을 겪습니다. 이러한 한계를 극복하고 주석 없는 데이터를 활용하기 위해, 셀프-슈퍼바이즈드 학습이 유망한 표현 학습 접근 방식으로 부상했습니다. 특히, 대조 학습 (CL)은 다양한 도메인에서 뛰어난 성능을 보여주었습니다. 그러나 표준 CL 목표는 유사한 TS 인스턴스 및 TS 내 인접 타임스탬프의 고유한 상관관계를 무시하여 TS 표현 학습에 해로울 수 있습니다. 이러한 문제를 해결하기 위해 우리는 시계열에 대한 소프트 대조 학습 전략인 SoftCLT를 제안합니다. SoftCLT는 인스턴스별 및 시간적 대조 손실을 위해 소프트 할당을 도입하여, 인스턴스 간 거리와 타임스탬프 간 차이를 기반으로 소프트 할당을 적용합니다. 이는 표준 대조 손실의 일반화로 볼 수 있으며, 제안된 방법이 이전 CL 방법보다 다양한 작업에서 성능을 향상시키는 것을 입증합니다. 우리의 주요 기여는 다음과 같습니다:

TS를 위한 소프트 대조 학습 전략 SoftCLT를 제안하여, 인스턴스 및 시간적 차원에서 소프트 대조 손실을 도입합니다.
다양한 TS 작업에서 SoftCLT의 효과를 입증하는 광범위한 실험 결과를 제공합니다.
SoftCLT는 다른 TS CL 프레임워크에 쉽게 적용 가능하며, 오버헤드가 거의 없습니다.
실험 결과, SoftCLT는 이전 CL 방법의 성능을 향상시키고 다양한 다운스트림 작업에서 최첨단 성능을 달성했습니다.

2.RELATED WORK

자기 지도 학습:
최근 자기 지도 학습은 대량의 라벨이 없는 데이터에서 강력한 표현을 학습하는 능력으로 많은 주목을 받았습니다. 이 방법은 데이터의 특정 측면에서 유도된 사전 과제를 해결하는 방식으로 모델을 훈련합니다. 자연어 처리에서는 다음 토큰 예측과 마스킹 토큰 예측이, 컴퓨터 비전에서는 퍼즐 맞추기와 회전 예측이 주로 사용됩니다. 특히, 대조 학습은 여러 도메인에서 효과적인 사전 과제로, 긍정 쌍의 유사성을 최대화하고 부정 쌍의 유사성을 최소화하는 방식입니다.

시계열 데이터에서의 대조 학습:
시계열 분석 분야에서는 여러 CL 방법이 제안되었으며, 각 방법은 시계열의 불변 속성을 고려해 긍정 및 부정 쌍을 정의합니다. 대표적인 방법으로 T-Loss, Self-Time, TNC, TS-SD, TS-TCC, CA-TCC, TS2Vec, Mixing-up, CoST, TimeCLR, TF-C, Subject-Aware CL, CLOCS 등이 있습니다. 이러한 기존 방법들은 모든 부정 쌍의 유사성을 동일하게 최소화하는 하드 대조 손실을 사용합니다.

소프트 대조 학습:
기존 CL 방법은 배치 인스턴스 구별을 통해 각 인스턴스를 별도의 클래스로 간주하지만, 이 접근 방식은 유사한 샘플을 임베딩 공간에서 멀리 떨어뜨릴 위험이 있습니다. 이를 해결하기 위해, 특징 거리와 기하학적 근접성을 기반으로 소프트 할당을 사용하는 방법, 특징 공간에서 추가적인 긍정 샘플을 정의하는 방법 등이 제안되었습니다. 그러나 비-시계열 도메인에서는 데이터 공간에서 인스턴스 간 유사성을 측정하기 어려워 임베딩 공간에서 소프트 할당을 계산합니다. 반면, 우리는 데이터 공간에서 시계열 인스턴스 간 거리를 기반으로 소프트 할당을 계산할 것을 제안합니다.

시계열 데이터에서의 마스킹 모델링:
대조 학습 외에도 마스킹 모델링은 시계열 데이터를 부분적으로 마스킹하고 누락된 값을 예측하는 사전 과제로 연구되고 있습니다. CL은 고수준 분류 작업에서 뛰어난 성능을 보였지만, 마스킹 모델링은 저수준 예측 작업에서 우수한 성과를 보였습니다. TST, PatchTST, SimMTM 등은 이러한 마스킹 모델링 패러다임을 채택하여 시계열 데이터를 재구성합니다.

3.METHODOLOGY

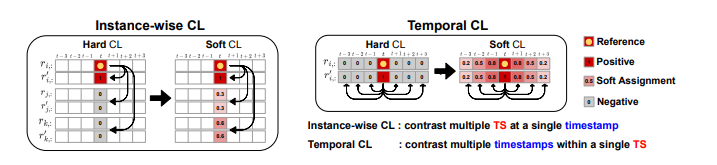
3.1 PROBLEM DEFINITION

이 논문은 배치된 N개의 시계열 X = {x1, . . . , xN }이 주어졌을 때, 비선형 임베딩 함수 fθ : x → r을 학습하는 과제를 다룹니다. 우리의 목표는 시계열 xi ∈ R^(T × D)을 표현 벡터 ri = [ri,1, . . . , ri,T]⊤ ∈ R^(T × M)로 매핑하는 fθ를 학습하는 것입니다. 여기서 T는 시퀀스 길이, D는 입력 특성 차원, M은 임베딩된 특성 차원을 나타냅니다

3.2 SOFT INSTANCE-WISE CONTRASTIVE LEARNING

배치 내 모든 인스턴스를 대조하는 것은 TS 표현 학습에 해로울 수 있습니다. 이는 유사한 인스턴스들이 임베딩 공간에서 멀리 떨어지도록 학습되기 때문입니다. 컴퓨터 비전과 같은 다른 도메인과 달리, 데이터 공간에서 계산된 TS 데이터 간의 거리는 유사성을 측정하는 데 유용합니다. 예를 들어, 두 개의 다른 이미지의 픽셀 간 거리는 일반적으로 유사성과 관련이 없지만, 두 TS 데이터의 거리는 유사성을 측정하는 데 유용합니다. 우리는 min-max 정규화된 거리 측정값 D(·, ·)를 사용하여 인스턴스별 대조 손실을 위한 소프트 할당을 정의합니다. 이때 시그모이드 함수 σ(a) = 1/(1 + exp(−a))를 사용합니다:

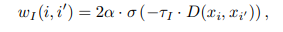
여기서 τ_I는 샤프니스(급변성)를 제어하는 하이퍼파라미터이고, α는 동일한 TS와 서로 가까운 다른 TS 쌍을 구분하기 위한 [0, 1] 범위의 상한값입니다. α = 1일 때, 거리가 0인 쌍과 동일한 TS 쌍에 1의 할당값을 부여합니다. TS 간의 거리는 증강된 뷰가 아닌 원래 TS로 계산됩니다. 이는 효율성을 위해 쌍별 거리 행렬을 오프라인에서 미리 계산하거나 캐시할 수 있기 때문입니다.

거리 측정값 D의 선택을 위해, 우리는 Table 6d에서 1) 코사인 거리, 2) 유클리드 거리, 3) 동적 시간 왜곡(DTW), 4) 시간 정렬 측정(TAM)을 비교하는 연구를 수행했습니다. 그 중 DTW를 거리 측정값으로 선택했습니다. DTW의 계산 복잡도는 길이가 T인 두 TS에 대해 O(T^2)이므로 대규모 데이터셋에서는 비용이 많이 들 수 있지만, 오프라인에서 미리 계산하거나 캐시하여 효율적인 계산을 촉진할 수 있으며, FastDTW와 같은 빠른 버전(O(T) 복잡도)을 사용할 수 있습니다. 우리는 DTW와 FastDTW의 출력이 거의 동일하며, CL 결과도 일치함을 경험적으로 확인했습니다.

간결성을 위해 ri,t = ri+2N,t 및 r˜i,t = ri+N,t을 xi의 두 가지 증강에서 타임스탬프 t의 임베딩 벡터로 정의합니다. 대조 손실이 교차 엔트로피 손실로 해석될 수 있다는 사실에서 영감을 받아, 손실을 계산할 때 고려되는 모든 유사성 중 상대적 유사성의 소프트맥스 확률을 다음과 같이 정의합니다:

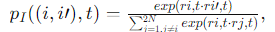
여기서 점곱을 유사성 측정값으로 사용합니다. 그러면 타임스탬프 t에서 xi의 소프트 인스턴스별 대조 손실은 다음과 같이 정의됩니다:

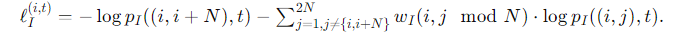
ℓ_{I}^{(i,t)}의 첫 번째 항은 긍정 쌍의 손실에 해당하며, 두 번째 항은 소프트 할당 w_I(i, i′)로 가중된 다른 쌍의 손실에 해당합니다. 이 손실은 모든 w_I(i, i′) = 0일 때 하드 인스턴스별 대조 손실의 일반화로 볼 수 있습니다.

SOFT TEMPORAL CONTRASTIVE LEARNING

다음의 직관에 따라 인접 타임스탬프의 값들이 유사하다는 것을 고려하여, 시간 대조 손실을 위한 소프트 할당을 타임스탬프 간의 차이에 기반하여 계산할 것을 제안합니다. 인스턴스별 소프트 대조 손실과 유사하게, 타임스탬프가 가까워지면 할당 값은 1에 가까워지고, 멀어지면 0에 가까워집니다. 시간 대조 손실을 위한 타임스탬프 쌍 (t, t′)의 소프트 할당을 다음과 같이 정의합니다:

여기서 τ_T는 샤프니스를 제어하는 하이퍼파라미터입니다. 타임스탬프 간의 근접도는 데이터셋마다 다르므로, 소프트 할당의 정도를 조절하기 위해 τ_T를 조정합니다. Figure 2a는 다른 τ_T 값에 따른 타임스탬프 차이에 대한 소프트 할당의 예를 보여줍니다.

Hierarchical loss

시간 대조 학습(temporal CL)을 위해, 이전 TS 대조 학습 방법에서와 같이 네트워크 fθ의 중간 표현에서 계층적 대조를 고려합니다. 구체적으로, TS2Vec (Yue et al., 2022)에서 제안된 계층적 대조 손실을 채택하여, 시간 축을 따라 각 최대 풀링(max-pooling) 레이어 이후의 중간 표현에서 손실을 계산하고 이를 합산합니다. Figure 2b에서 보여주듯이, 풀링 후 인접한 시간 단계 사이의 유사성이 감소하므로, τ_T를 조정하여 풀링 레이어의 커널 크기 m과 깊이 k를 곱하여 조정합니다. 즉, τ_T = m^k · τ˜_T, 여기서 τ˜_T는 기본 하이퍼파라미터입니다. 이제, ri,t = ri,t+2T 및 r˜i,t = ri,t+T로 xi의 두 가지 증강에서 타임스탬프 t의 임베딩 벡터를 정의합니다. 식 (2)와 유사하게, 손실을 계산할 때 고려된 모든 유사성 중 상대적 유사성의 소프트맥스 확률을 다음과 같이 정의합니다:

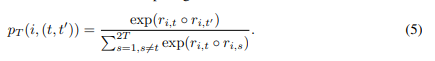
위의 SOFT INSTANCE-WISE CONTRASTIVE LEARNINGSMS -> OFFLINE방식으로 시계열간의 유사성을 측정하여 유사성이 높은것은 Negative Pair의 가중치를 작게함.

즉, Hierarchical Loss는 거리가 인접할수록 유사성이 높다는 가정하에 Negative Pair의 가중치를 작게함.

Experiment

우리는 제안된 방법의 유효성을 검증하고 다양한 과제에서의 성능을 평가하기 위해 광범위한 실험을 수행합니다: (1) 단변량 및 다변량 시계열(TS) 분류, (2) (i) 셀프-슈퍼바이즈드 학습 후 파인 튜닝 및 (ii) 세미-슈퍼바이즈드 학습을 통한 세미-슈퍼바이즈드 분류, (3) 도메인 내 및 도메인 간 시나리오에서의 전이 학습, 그리고 (4) 정상 및 콜드 스타트 설정에서의 이상 탐지. 우리는 또한 SoftCLT의 유효성과 설계 선택의 효과를 검증하기 위해 소거 연구(ablation studies)를 수행합니다. 마지막으로, 이전 방법에 대한 SoftCLT의 효과를 보여주기 위해 쌍별 거리 행렬과 t-SNE (Van der Maaten & Hinton, 2008)로 시간 표현을 시각화합니다. 우리는 SoftCLT를 적용하는 방법에 대한 데이터 증강 전략을 사용합니다: TS2Vec은 겹치는 TS 세그먼트로 두 개의 뷰를 생성하고, TS-TCC/CA-TCC는 약한 증강과 강한 증강을 사용하여 두 개의 뷰를 생성하며, 각각 진동 및 스케일(Jitter-and-Scale)과 순열 및 진동(Permutation-and-Jitter) 전략을 사용합니다.

CLASSIFICATION

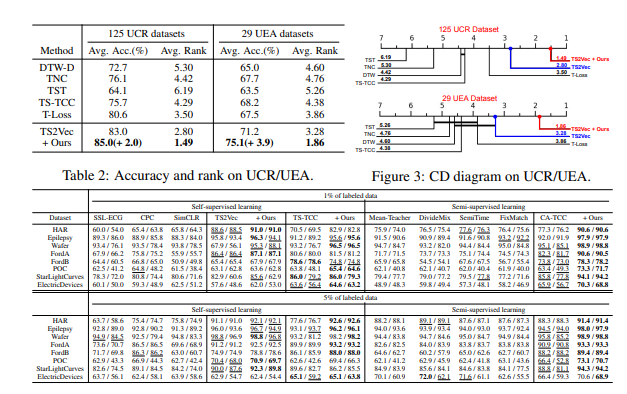
우리는 단변량 시계열(TS)을 위해 1251개의 UCR 아카이브 데이터셋(Dau et al., 2019)과 다변량 TS를 위해 292개의 UEA 아카이브 데이터셋(Bagnall et al., 2018)에서 TS 분류 작업에 대한 실험을 수행했습니다. 구체적으로, 우리는 TS2Vec(Yue et al., 2022)에 SoftCLT를 적용했습니다. 이는 위의 데이터셋에서 SOTA 성능을 입증한 방법입니다. 기준 방법으로는 DTW-D(Chen et al., 2013), TNC(Tonekaboni et al., 2021), TST(Zerveas et al., 2021), TS-TCC(Eldele et al., 2021), T-Loss(Franceschi et al., 2019), TS2Vec(Yue et al., 2022)를 고려했습니다. 실험 프로토콜은 T-Loss와 TS2Vec의 프로토콜을 따랐으며, 모든 타임스탬프의 맥스 풀링 표현에서 얻은 인스턴스 수준 표현 위에 SVM 분류기를 RBF 커널로 훈련했습니다.

실험 결과, Table 2와 Figure 3의 Wilcoxon-Holm 방법(Ismail Fawaz et al., 2019)에 기반한 중요한 차이(CD) 다이어그램은 제안된 방법이 두 데이터셋 모두에서 정확도와 순위 측면에서 SOTA 성능을 상당히 향상시킴을 보여줍니다. Figure 3에서는 각 데이터셋의 최상위 및 차상위 결과를 각각 빨간색과 파란색으로 표시했습니다. 또한, 평균 순위의 차이가 95% 신뢰 수준에서 통계적으로 유의미하지 않은 경우, 굵은 선으로 연결하여 제안된 방법의 성능 향상이 유의미함을 나타냈습니다.

SEMI-SUPERVISED CLASSIFICATION

우리는 SoftCLT를 TS-TCC(Eldele et al., 2021)와 그 확장 버전인 CA-TCC(Eldele et al., 2023)에 적용하여 세미-슈퍼바이즈드 분류 작업에 대한 실험을 수행했습니다. TS-TCC와 CA-TCC는 각각 셀프 및 세미-슈퍼바이즈드 학습에 대조 학습(CL)을 통합한 방법입니다. 기준 방법으로는 셀프-슈퍼바이즈드 학습을 위해 SSL-ECG(Sarkar & Etemad, 2020), CPC(Oord et al., 2018), SimCLR(Chen et al., 2020), TS-TCC(Eldele et al., 2021)를, 세미-슈퍼바이즈드 학습을 위해 Mean-Teacher(Tarvainen & Valpola, 2017), DivideMix(Li et al., 2020), SemiTime(Fan et al., 2021), FixMatch(Sohn et al., 2020), CA-TCC(Eldele et al., 2023)를 고려했습니다. TS-TCC와 CA-TCC는 인스턴스별 및 시간 대조를 수행하지만, 이들의 시간 대조는 한 뷰의 미래를 다른 뷰로부터 예측하는 방식으로, 일반적인 대조 손실과는 다릅니다. 따라서 우리는 두 방법에 소프트 시간 대조 손실을 추가적인 손실로 채택했습니다.

평가를 위해 CA-TCC의 실험 설정과 데이터셋을 사용했으며, 여기에는 8개의 데이터셋(Anguita et al., 2013; Andrzejak et al., 2001; Dau et al., 2019)이 포함됩니다. 이 중 6개는 UCR 아카이브에서 가져온 것입니다. 우리는 두 가지 세미-슈퍼바이즈드 학습 시나리오를 고려했습니다: (1) 라벨이 없는 데이터로 셀프-슈퍼바이즈드 학습을 수행한 후 라벨이 있는 데이터로 슈퍼바이즈드 파인튜닝을 수행하는 경우와 (2) 라벨이 있는 데이터와 라벨이 없는 데이터를 함께 사용하는 세미-슈퍼바이즈드 학습입니다. Table 3은 1% 및 5% 라벨이 있는 데이터셋 시나리오에서 두 방법의 실험 결과를 보여주며, SoftCLT를 적용하면 대부분의 데이터셋에서 두 시나리오 모두에서 전반적으로 최고의 성능을 달성함을 보여줍니다.

TRANSFER LEARNING

우리는 이전 연구(Zhang et al., 2022; Eldele et al., 2021; 2023; Dong et al., 2023)에서 사용된 도메인 내 및 도메인 간 설정에서 분류를 위한 전이 학습 실험을 수행했습니다. SoftCLT를 TS-TCC와 CA-TCC에 적용했습니다. 기준 방법으로는 TS-SD(Shi et al., 2021), TS2Vec(Yue et al., 2022), Mixing-Up(Wickstrøm et al., 2022), CLOCS(Kiyasseh et al., 2021), CoST(Woo et al., 2022), LaST(Wang et al., 2022), TF-C(Zhang et al., 2022), TS-TCC(Eldele et al., 2021), TST(Zerveas et al., 2021), SimMTM(Dong et al., 2023)를 고려했습니다. 도메인 내 전이 학습에서는 SleepEEG(Kemp et al., 2000)에서 사전 학습을 수행하고, Epilepsy(Andrzejak et al., 2001)에서 파인튜닝을 합니다. 두 데이터셋 모두 EEG 데이터셋으로 유사한 도메인으로 간주됩니다. 도메인 간 전이 학습에서는 하나의 데이터셋에서 사전 학습을 하고 다른 데이터셋에서 파인튜닝을 수행합니다. SleepEEG에서 사전 학습을 하고, 다른 도메인인 FD-B(Lessmeier et al., 2016), Gesture(Liu et al., 2009), EMG(Goldberger et al., 2000)에서 파인튜닝을 수행합니다. 또한, 셀프 및 세미-슈퍼바이즈드 설정에서 적응 없이 전이 학습을 수행합니다. 소스 및 타겟 데이터셋이 동일한 클래스 집합을 공유하지만 소스 데이터셋의 1% 라벨만 사용할 수 있고 타겟 데이터셋에서는 추가 훈련이 허용되지 않습니다. 구체적으로, Fault Diagnosis (FD) 데이터셋(Lessmeier et al., 2016)에서 네 가지 조건(A,B,C,D) 중 하나에서 모델을 훈련하고 다른 조건에서 테스트합니다. Table 4a는 도메인 내 및 도메인 간 전이 학습 결과를 보여주고, Table 4b는 FD 데이터셋으로 셀프 및 세미-슈퍼바이즈드 설정에서의 결과를 보여줍니다. 특히, CA-TCC에 SoftCLT를 적용하면 FD 데이터셋의 12개 전이 학습 시나리오에서 평균 정확도가 10.68% 향상됩니다.

Anomaly Detection

우리는 단변량 TS 이상 탐지(AD) 작업에서 SoftCLT를 TS2Vec(Yue et al., 2022)에 적용하여 두 가지 설정에서 실험을 수행했습니다. 정상 설정에서는 각 데이터셋을 시간 순서에 따라 두 부분으로 나누어 각각 훈련과 평가에 사용합니다. 콜드 스타트 설정에서는 UCR 아카이브의 FordA 데이터셋에서 모델을 사전 학습하고 각 데이터셋에서 평가를 수행합니다. 기준 방법으로는 정상 설정에서 SPOT(Siffer et al., 2017), DSPOT(Siffer et al., 2017), DONUT(Xu et al., 2018), SR(Ren et al., 2019)를, 콜드 스타트 설정에서 FFT(Rasheed et al., 2009), Twitter-AD(Vallis et al., 2014), Luminol(LinkedIn, 2018)를, 두 설정 모두에서 TS2Vec(Yue et al., 2022)를 고려했습니다. 이상 점수는 TS2Vec을 따라 마스킹된 입력과 마스킹되지 않은 입력에서 인코딩된 두 표현의 L1 거리를 통해 계산됩니다. 우리는 Yahoo(Laptev et al., 2015)와 KPI(Ren et al., 2019) 데이터셋에서 비교 방법을 평가했습니다. 인스턴스별 대조 학습을 억제하면 평균적으로 더 나은 AD 성능을 얻을 수 있음을 발견했으며, 따라서 인스턴스별 대조 학습 없이 TS2Vec과 SoftCLT 성능을 보고했습니다. 더 자세한 내용은 부록 G에서 확인할 수 있습니다. Table 5에 나타난 바와 같이, SoftCLT는 두 설정 모두에서 F1 점수, 정밀도, 재현율 측면에서 기준 방법을 능가했습니다. 특히, TS2Vec에 SoftCLT를 적용하면 두 데이터셋에서 정상 설정과 콜드 스타트 설정 모두에서 F1 점수가 약 2% 향상되었습니다.