Abstract

PCA, LDA, T-SNE와 같은 전통적인 클러스터링 방법은 복잡한데이터를 다룰 때 효과적이지 않습니다. 최근 연구들은 딥 뉴럴 네트워크를 사용한 비선형 차원 축소와 하드 파티션 클러스터링을 결합하여 더 나은 결과를 달성했습니다. 그러나 이러한 방법들은 차원 축소와 클러스터링의 파라미터를 동시에 업데이트할 수 없습니다.

연구는 소프트 파티션 클러스터링과 딥 임베딩을 결합한 솔루션을 소개합니다. 구체적으로, 퍼지 c-평균 (FCM) 알고리즘을 사용합니다. FCM의 멤버십 기능은 하드 파티션 클러스터링의 이산 할당 프로세스로 인해 발생하는 그래디언트 강하 구현 문제를 해결합니다. 이 접근 방식은 딥 뉴럴 네트워크 파라미터와 클러스터 중심을 동시에 업데이트할 수 있게 합니다.

이 연구의 혁신적인 측면은 소프트 파티션 클러스터링과 딥 임베딩을 결합한 연속 목적 함수를 생성하는 것입니다. 이를 통해 학습 표현이 클러스터링에 유리하도록 보장합니다. 실험 결과는 이러한 통합 접근 방식이 별도로 최적화하는 것보다 동시에 딥 차원 축소 및 클러스터링 파라미터를 최적화하는 것이 더 효과적임을 보여줍니다.

Introduction

클러스터링의 목표는 샘플 특성의 유사성에 기반하여 데이터를 여러 범주로 분류하는 것입니다. 클러스터 분석은 텍스트 마이닝, 생물정보학, 이미지 처리, 패턴 인식, 통계 학습 등 여러 분야에 적용되고 있습니다. 전통적인 클러스터링 알고리즘에는 프로토타입 클러스터링, 계층적 클러스터링, 밀도 클러스터링이 있으며, 이 중 k-평균 알고리즘은 가장 널리 사용되는 하드 파티션 클러스터링 알고리즘입니다.

그러나 사진과 대형 텍스트와 같은 복잡한 데이터를 다룰 때 이러한 클러스터링 알고리즘들은 차원의 저주로 인해 성능이 좋지 않습니다. 최근에는 PCA, LDA, T-SNE와 같은 차원 축소 방법들이 제안되었지만, 이러한 방법들은 원래 데이터에서 저차원 공간으로의 복잡한 매핑을 만들 수 없습니다. 실제 데이터는 복잡한 비선형 차원 축소를 필요로 하며, 최근 연구된 딥 뉴럴 네트워크(DNN)는 복잡한 비선형 매핑을 수행할 수 있습니다.

이 논문에서는 오토인코더와 함께 소프트 파티션 클러스터링을 결합하여 하드 파티션 클러스터링의 이산성으로 인한 그라디언트 업데이트 문제를 해결합니다. 소프트 파티션 클러스터링의 멤버십 정도를 업데이트 가능한 그라디언트 항으로 사용하여 클러스터링을 DNN 차원 축소와 결합하므로, 오토인코더와 클러스터링의 파라미터를 동시에 업데이트할 수 있게 합니다. FCM, MEC, FC-QR과 같은 소프트 파티션 클러스터링 알고리즘은 DNN 차원 축소와 이론적으로 결합될 수 있지만, FC-QR 알고리즘은 멤버십 정도 업데이트 시 연속성이 부족하므로, 연속적인 그라디언트를 달성할 수 있는 FCM 및 MEC를 사용합니다.

• DNN 차원 축소와 소프트 파티션 클러스터링을 결합하여 전체 네트워크 파라미터의 동시 최적화를 제안합니다.
• 소프트 클러스터링을 차별화 가능하게 만들어, 클러스터 중심과 DNN 파라미터를 동시에 업데이트할 수 있게 합니다.
• 복잡한 이미지 및 텍스트 데이터 세트를 사용하여 방법의 효과를 검증합니다.

Related Work

Fuzzy C Means (FCM)

데이터 포인트가 하나의 클러스터에만 전적으로 속하는 대신, 여러 클러스터에 속할 수 있는 확률 또는 멤버십을 갖습니다. FCM의 주요 단계는 다음과 같습니다:

초기화: 클러스터의 수 C를 선택하고, 각 클러스터에 대한 중심을 무작위로 초기화합니다. C는 사용자가 정한 값으로, 데이터를 그룹화하고자 하는 클러스터의 수를 나타냅니다.

멤버십 할당: 각 데이터 포인트에 대해, 모든 클러스터 중심과의 거리를 계산하고, 이 거리를 기반으로 멤버십(소속도)를 할당합니다. 멤버십 값은 0과 1 사이의 값으로, 데이터 포인트가 클러스터 중심에 가까울수록 높은 값을 가집니다.

클러스터 중심 갱신: 할당된 멤버십 값을 바탕으로 각 클러스터의 중심을 갱신합니다. 이는 모든 데이터 포인트의 위치에 가중치를 두어 평균을 낸 것으로, 멤버십 값이 클수록 해당 데이터 포인트의 영향이 큽니다.

반복: 멤버십 할당과 클러스터 중심 갱신을 반복하여 수렴할 때까지 계속합니다. 수렴 조건은 일반적으로 멤버십 값의 변화가 특정 임계값 아래로 떨어지거나, 반복 횟수가 사전에 정한 최대 횟수에 도달했을 때로 설정됩니다.

최종 클러스터링 결과: 알고리즘이 수렴하면, 각 데이터 포인트는 하나 이상의 클러스터에 소속될 수 있으며, 소속도가 가장 높은 클러스터로 분류됩니다.

퍼지 C-평균 클러스터링은 데이터 포인트가 여러 클러스터에 부분적으로 속할 수 있는 현실 세계의 여러 시나리오에 적합합니다. 이 방법은 데이터가 뚜렷하게 구분되지 않고 중첩되는 경우에 특히 유용합니다.

Deep soft clustering

Deep FCM

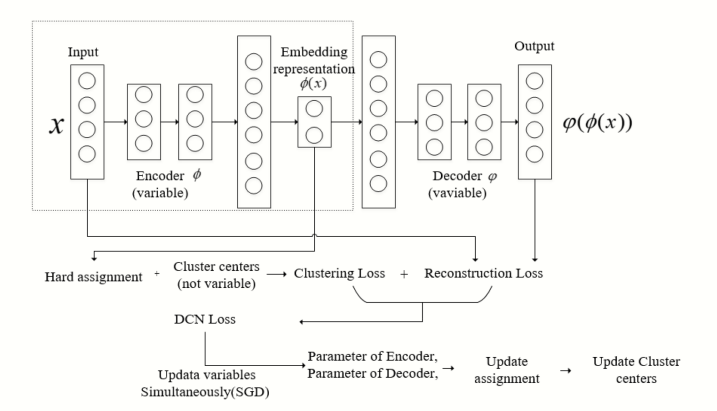
DCN 구조를 기반으로, 클러스터링 부분의 불연속적인 하드 할당을 퍼지 클러스터링의 멤버십 정도에 따른 소프트 할당으로 대체하여 클러스터 중심과 오토인코더의 파라미터를 동시에 최적화할 수 있습니다.

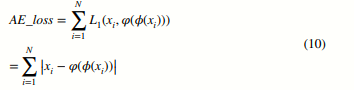
xi는 데이터 세트 X = {x1, …, xN}의 샘플을 나타내며, N은 샘플의 수입니다. FCM 손실 함수 부분에서, 우리는 인코더를 사용하여 원래 데이터 xi를 클러스터 친화적인 저차원 데이터 인코더(xi)로 매핑합니다.

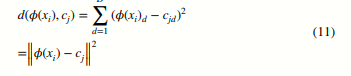
C = {c1, …, cK}는 클러스터 중심이며 K는 클러스터의 수입니다. d(인코더(xi), cj)는 차원 축소 후 샘플 인코더(xi)과 클러스터 중심 cj 사이의 제곱 유클리드 거리입니다. 여기서 D는 차원 축소 후 샘플의 차원이며, 클러스터 중심의 차원과도 같습니다. 인코더(xi) d는 차원 축소 후 ith 샘플의 d번째 차원을, cjd는 j번째 클러스터 중심의 d번째 차원을 나타냅니다.

그런 다음 클러스터 중심과 축소된 차원의 샘플을 사용하여 소프트 할당을 위한 멤버십 정도를 계산합니다. 멤버십 정도의 계산 공식은 다음과 같습니다:

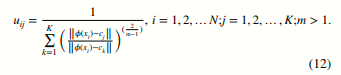
여기서 uij는 차원 축소 후 샘플 인코더(xi)가 클래스 중심 cj에 속할 확률을 나타내며, m은 퍼지화 수준 지수입니다. 위의 멤버십 소프트 할당과 클러스터링 거리 계산을 결합하여, 다음과 같은 클러스터링 손실을 제안합니다:

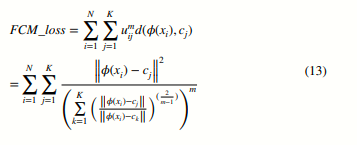
식 (10)과 식 (13)을 결합하여, Deep-FCM 모델은 다음과 같이 표현될 수 있습니다:

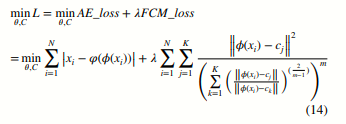
알고리즘의 전체 네트워크 구조는 그림 2에서 보여줍니다. 알고리즘 1은 딥 퍼지 C-평균 알고리즘의 구체적인 절차를 제공하며, 여기서 m1, m2, …, mn은 퍼지 클러스터링의 값 세트입니다.

Deep MEC

퍼지 C-평균(FCM)을 기반으로, 최대 엔트로피 클러스터링(MEC)은 멤버십의 엔트로피를 정규화 항으로서 목적 함수에 포함시키는데, 이는 다른 소프트 할당 클러스터링 방법입니다. 비교를 위해, 우리는 MEC와 오토인코더를 결합합니다. 오토인코더 부분의 손실 함수는 섹션 3.1의 Deep-FCM에서와 동일하며, FCM 부분은 다음 공식으로 대체됩니다:

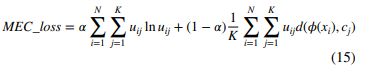
Deep FCM과의 또 다른 차이점은 여기서 멤버십 정도의 계산 공식입니다:

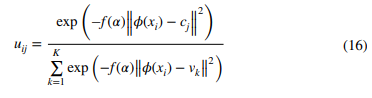
식 (10)과 식 (15)를 결합하여, Deep-MEC 모델은 다음과 같이 표현됩니다:

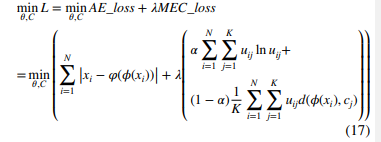
Deep-MEC의 네트워크 구조는 그림 2의 Deep-FCM과 동일하지만, 멤버십 및 클러스터링 손실의 계산 방법에 차이가 있습니다. 알고리즘 2는 각각 딥 퍼지 C-평균과 딥 최대 엔트로피 클러스터링 알고리즘의 구체적인 절차를 제공합니다. 여기서는 퍼지 클러스터링 가중치 지수와 퍼지 파라미터 값 세트입니다.

Parameter

DeepFCM에서 조정해야 할 하이퍼파라미터는 m과 휆입니다. 휆은 클러스터링 손실과 오토인코더 재구성 손실의 비율을 전체 손실 함수에서 조절하는 데 사용됩니다. m이 클수록 클러스터링 손실의 비율이 커집니다. m의 값에 관해서는, m = 1일 때 FCM은 더 이상 소프트 파티션 알고리즘으로 작동하지 않고 하드 파티션 방법으로 저하되며, 이는 K-평균 알고리즘과 동일합니다. 이 증명은 간단하며, 부록 자료에서 자세히 설명되어 있습니다. m → +∞으로 갈수록 FCM 알고리즘의 멤버십 정도는 효과를 잃게 되며, 모든 멤버십 정도는 클러스터 수의 역수와 같은 값이 됩니다. 따라서 m의 값이 커질수록 클러스터 할당의 퍼지 정도가 높아집니다. Deep MEC에서 훼의 선택에 관해서는, 훼 = 1일 때, (1 - 훼)∕훼는 0과 같습니다. 이 때, 위의 경우와 마찬가지로 모든 멤버십 정도는 고정된 값이 되며, 이는 클러스터 수의 역수와 같습니다.

Experiment

Dataset

고차원 데이터 처리에 있어서 전통적인 클러스터링 알고리즘보다 우리가 제안한 알고리즘의 우수성을 보여주기 위해, 이미지 데이터셋과 텍스트 데이터셋을 포함한 세 개의 고차원 데이터셋을 사용했습니다. MNIST 데이터셋은 손으로 쓴 숫자들의 70,000개의 흑백 이미지로 구성되어 있으며, 0부터 9까지의 10개 카테고리를 포함하고 있습니다. 각 이미지는 28×28 픽셀로 구성되어 있으며, 데이터셋은 60,000개의 이미지를 포함하는 트레인 데이터셋과 10,000개의 이미지를 포함하는 테스트 데이터셋으로 나뉩니다. USPS 데이터셋 또한 손으로 쓴 숫자 이미지 데이터셋으로, 7,291개의 트레이닝 이미지와 2,007개의 테스트 이미지를 포함하고 있으며, 이미지 크기는 16×16 픽셀입니다. 20NEWS 데이터셋은 영어 뉴스 데이터셋으로, 20,000개의 뉴스 문서를 포함하며 총 20개의 카테고리로, 12,000개는 트레이닝 데이터셋으로, 8,000개는 테스트 데이터셋으로 사용됩니다. MNIST 및 USPS 데이터셋의 이미지 데이터를 각각 784차원 벡터와 256차원 벡터로 변환합니다. 반면에, 20NEWS의 각 기사를 후속 계산을 위해 2000차원의 TF-IDF 벡터로 변환합니다.

Result analysis

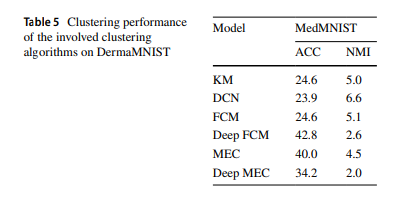
클러스터링에서 일반적으로 사용되는 두 가지 성능 평가 지표인 클러스터링 정확도(ACC)와 정규화된 상호 정보(NMI)를 사용했습니다. 두 지표 모두 0에서 1 사이의 값을 가지며, 값이 클수록 클러스터링 방법의 효과가 더 좋습니다. 위에서 언급한 여섯 가지 클러스터링 방법의 세 데이터셋에 대한 클러스터링 효과는 표 1에서 보여줍니다. 표의 값은 모두 백분율 값입니다. 딥 차원 축소 후 DCN, Deep-FCM, Deep-MEC의 효과가 차원 축소를 하지 않은 전통적인 클러스터링 방법 K-means, FCM, DEC보다 현저히 높은 것을 명확하게 볼 수 있습니다. Deep-FCM 알고리즘의 세 데이터셋에 대한 성능은 딥 차원 축소와 하드 클러스터링을 결합한 최신 방법인 DCN보다 높습니다. 이는 소프트 클러스터링을 딥 차원 축소와 결합하여 클러스터링 센터와 오토인코더 네트워크의 파라미터를 동시에 업데이트할 수 있는 우리의 제안된 방법이 차원 축소 후 데이터가 클러스터링 요구 사항을 더 잘 충족시킬 수 있음을 증명합니다(표 2).

섹션 3.2에서 언급한 세 가지 하이퍼파라미터는 다음과 같이 알고리즘에 다른 영향을 미칩니다: 그림 4에서 볼 수 있듯이 m 값을 어떻게 선택하든 Deep-FCM 알고리즘은 FCM 알고리즘보다 낫습니다. 앞서 언급했듯이 값이 작을수록 클러스터링 알고리즘이 하드 점수에 가까워집니다. MNIST와 USPS 이미지 데이터셋에서 전통적인 FCM 알고리즘이 더 나은 효과를 나타내며, 20NEWs 텍스트 데이터셋에서는 알고리즘이 1.6 근처에서 최고 성능을 보입니다. MNIST와 USPS 이미지 데이터셋에서 Deep-FCM 알고리즘의 성능은 [1.0, 1.6] 구간에서 크게 변하지 않습니다. [1.6, 2.0] 구간에서는 지수가 증가함에 따라 작아지며, 20NEWs 텍스트 데이터셋에서는 [1.0, 1.3] 구간에서 알고리즘의 성능이 크게 변하지 않지만, [1.3, 2.0] 구간에서는 증가함에 따라 감소하고 1.4 이상이 되면 알고리즘은 기본적으로 실패합니다. 특히 1에 가까울 때 FCM 알고리즘이 이론적으로 K-means로 퇴화되지만, 실험에서 값이 너무 커서 효과적인 결과를 얻지 못합니다.

MEC 알고리즘은 세 데이터셋에서 다른 값에 대해 기본적으로 동일한 성능을 보입니다.

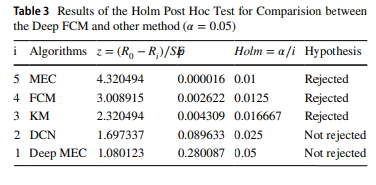
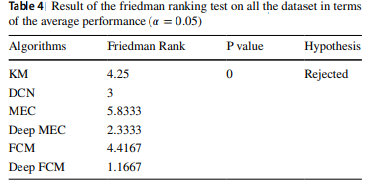
비모수적인 프리드만 순위 테스트(Demšar 2006; Garcia and Herrera 2008)와 홀름 후행 검정(Demšar 2006; Garcia and Herrera 2008)은 모든 방법들 간의 성능을 비교하는 데 사용됩니다. 홀름 후행 검정은 최적의 프리드만 순위를 얻는 방법이 다른 비교 방법들과 통계적으로 유의미하게 다른지를 검증하는 데 사용될 수 있습니다. 프리드만 순위 테스트는 다양한 방법들의 평균 순서를 계산하여 일련의 방법들 사이에 유의미한 차이가 있는지를 결정하는 데 사용될 수 있습니다. 홀름 후행 검정과 프리드만 순위 테스트 결과는 각각 표 3과 4에 요약되어 있습니다. 표 4의 결과는 Deep FCM과 다른 비교 방법들 간에 클러스터링 정확도에서 유의미한 차이가 있다는 것을 보여줍니다.