Abstract

매일 엄청난 양의 데이터가 빠른 속도로 생성되고 있습니다. 그 결과, 세계는 급증하는 데이터를 관리하는 데 있어 전례 없는 도전과 기회를 맞이하고 있습니다. 이러한 도전은 시계열 데이터에서 특히 두드러집니다. 분명히 대규모 시계열 데이터베이스를 효율적으로 탐색할 수 있는 솔루션이 절실히 필요합니다. 이러한 데이터 마이닝 작업 중 하나가 주기성 탐지입니다. 빅데이터에서 효율적이고 효과적인 주기성 탐지 기술은 동물의 이주 패턴 발견, 주기적인 주식 시장 데이터 분석, 심전도(ECG)에서 이상치 탐지, 주기적인 질병 발생 분석 등에서 유용할 것입니다. 이 연구는 대략적인 주기 감지를 위한 시계열 모티프의 개념을 활용합니다. 구체적으로, 우리는 반복 패턴에 기반하여 시계열 데이터에서 주기를 감지하는 새로운 간단한 방법을 제시합니다. 우리의 접근 방식은 효과적이고, 노이즈에 강하며, 효율적입니다. 실험 결과, 우리의 접근 방식은 정확성 면에서 널리 사용되는 주기 감지 기술보다 우수하며, 시간과 공간을 훨씬 적게 요구함을 보여줍니다.

Introduction

주기성은 일정한 간격으로 반복되는 패턴의 경향을 의미하며, 이는 여러 자연 현상이나 인간 활동에서 발생합니다. 예를 들어, 직원의 일일 작업 일정, 동물의 연간 이주 패턴, 지역의 태양 흑점 주기 등이 있습니다. 이러한 데이터는 너무 크고 복잡하여 전통적인 데이터베이스 관리 도구나 데이터 처리 응용 프로그램으로 처리하기 어렵습니다. 이러한 데이터를 빅데이터라고 합니다. 우리는 빅데이터 시대에 살고 있으며, 이는 인터넷과 일상 생활의 일부가 된 유비쿼터스 컴퓨팅 장치들로부터 얻어지는 엄청난 양의 데이터로 인해 더욱 강조되고 있습니다.

데이터, 크든 작든, 주기를 감지하는 것은 데이터에 대한 유용한 통찰을 제공하고, 더 나은 예측을 하며, 이상을 감지하고, 유사성 매칭을 개선하는 데 도움이 됩니다. 특히, 이 연구는 시계열 데이터에 중점을 두어 멀티미디어와 같은 다른 종류의 데이터에도 적합하며, 이는 시계열로 변환될 수 있습니다. 예를 들어, 오디오에서 MFCC를 추출하여 실험에 사용된 데이터셋 중 하나로 사용되는 경우가 있습니다.

여러 방법이 데이터에서 주기를 감지하기 위해 제안되었습니다. 대부분의 기존 방법은 완벽한 주기에 적합하지만, 이는 대부분의 자연 현상에서는 거의 발생하지 않습니다. 실제 데이터셋의 주기는 일반적으로 노이즈가 많고 불완전합니다. 따라서, 우리의 솔루션과 같은 견고한 근사 주기 감지 방식이 필요하며, 많은 응용 프로그램에서 근사 솔루션이 충분하다는 것이 입증되었습니다.

일반적으로 시계열에서 감지할 수 있는 주기 패턴에는 세 가지 유형이 있습니다:

부분 주기성: 적어도 하나의 기호와 하나의 가변 기호가 주기적인 경우.
기호 주기성: 최대 하나의 기호가 주기적으로 반복되는 경우.
세그먼트 주기성: 전체 패턴이 주기적인 경우.
대부분의 기술은 이산 시퀀스에 적합하지만, 시계열은 실수 값 데이터입니다. 따라서, 시계열 데이터를 기호화된 표현으로 변환하는 전처리 단계가 필요합니다. 표준 전처리 방법은 SAX(Symbolic Aggregate approXimation)를 사용하여 시계열을 문자열로 변환하는 것입니다.

""" 기호 (Symbol)
기호는 데이터 시퀀스 내의 특정 값이나 문자입니다. 예를 들어, 시계열 데이터가 "A, B, C, D"와 같은 문자로 이루어졌다면, A, B, C, D 각각이 기호입니다. 숫자로 된 데이터라면, 1, 2, 3, 4 등이 기호가 됩니다.

부분 주기성 (Partial Periodicity)
부분 주기성은 데이터 시퀀스 내에서 적어도 하나의 고정된 기호와 적어도 하나의 가변 기호가 주기적으로 나타나는 경우를 말합니다.

예시:
시계열 T = wxyz wxxy wxyy wxwz

여기서 "wx"는 고정된 기호이고, 나머지 "y"와 "z"는 가변 기호입니다.
wx * 는 부분 주기 패턴을 형성합니다. (여기서 는 가변 기호를 의미)
기호 주기성 (Symbol Periodicity)
기호 주기성은 시퀀스 내에서 최대 하나의 기호가 주기적으로 반복되는 경우를 말합니다.

예시:
시계열 T = xyz xzy xxy xyy

여기서 "x" 기호가 주기적으로 나타납니다.
주기 p = 3
세그먼트 주기성 (Segment Periodicity)
세그먼트 주기성은 시퀀스 전체 패턴이 주기적으로 반복되는 경우를 말합니다.

예시:
시계열 T = wxyz wxyz wxyz wxyz

여기서 전체 패턴 "wxyz"가 반복됩니다.
주기 p = 4
차이점 요약
부분 주기성: 적어도 하나의 고정된 기호와 적어도 하나의 가변 기호가 주기적으로 나타나는 경우 (예: w).
기호 주기성: 단일 기호가 주기적으로 반복되는 경우 (예: x x ** x).
세그먼트 주기성: 전체 패턴이 주기적으로 반복되는 경우 (예: wxyz wxyz).
이 예시를 통해 각 주기성의 차이점을 이해하는 데 도움이 되길 바랍니다. """

이 연구에서는 데이터로부터 반복 패턴(모티프)을 학습하여 시계열 데이터의 주기를 감지하는 새로운 기술을 제안합니다. 우리가 아는 한, 이 연구는 모티프 발견을 주기 감지 수단으로 사용하는 최초의 연구입니다. GrammarViz1 알고리즘을 기반으로 하는 우리의 접근 방식은 단순하고, 공간 및 시간 효율적이며, 가변 길이 모티프를 감지할 수 있는 능력을 가지고 있습니다.

요약하자면, 우리는 간단하고 우아한 근사 주기 감지 알고리즘인 모티프 기반 주기 감지(MBPD)를 제안합니다. 우리의 연구는 다음과 같은 새로운 기여를 합니다:

시계열 모티프 발견을 주기 감지의 전 단계로 사용합니다.
알고리즘은 시간 및 공간 효율적이며, 스트리밍 데이터에 적합합니다.
가장 중요한 주기를 순위 매기는 간단한 방법을 도입합니다.
GrammarViz를 확장하여 사용자가 탐색하고 감지된 주기를 정렬할 수 있는 주기 시각화 기능을 구현했습니다.
합성 및 실제 데이터셋에서 다른 인기 있는 기술들과 비교하여 우리의 기술의 성능을 실험했습니다.

Related Work

기존의 주기성 감지 방법은 여러 요인에 따라 분류될 수 있습니다. 이 요인에는 매개변수 의존성, 감지된 주기성의 유형, 감지된 주기성의 범위 및 주기성이 감지되는 도메인이 포함됩니다. 일부 방법은 주기 값을 명시해야 합니다. 이는 이상적이지 않은데, 주기 값을 감지하는 것도 중요한 과제이기 때문입니다. 일부 방법은 기호 주기성만 감지합니다. Yang 등은 시계열에서 잠재적 주기를 발견하기 위한 선형 시간 거리 기반 기술을 제안했으나, 인접한 간격만 고려하여 일부 유효한 주기를 감지하지 못합니다. Rasheed 등은 접미사 트리를 사용하여 시계열의 주기성을 감지하는 알고리즘을 제안했으나, 이 방법은 시간이 O(n^3)까지 증가할 수 있습니다.

대부분의 알고리즘은 앞서 언급한 주기성 유형(기호, 시퀀스, 세그먼트) 중 일부만 감지합니다. Han 등은 세그먼트 주기성만 감지하는 방법을 제안했습니다. 다른 특정 기술은 시계열에서 시퀀스 주기성을 감지하는 데 적합합니다. 이러한 기술 대부분은 노이즈에 민감합니다. WARP는 노이즈에 강하지만 세그먼트 주기성만 감지합니다. 몇 가지 기술은 부분 주기성을 감지하고, 대부분은 전체 주기성 감지에 중점을 둡니다.

주기성 감지 알고리즘은 시간 도메인 방법과 주파수 도메인 방법으로 분류될 수 있습니다. 시간 도메인 방법은 자기상관 함수에 기반하며, 주파수 도메인 방법은 스펙트럼 밀도 함수에 기반합니다. 시간 도메인 방법은 주기 데이터의 자기상관 함수가 데이터와 동일한 주기를 가지며 t=0, 주기 T 및 T의 배수에서 피크를 얻는다는 전제를 가지고 있습니다. 시간 도메인 방법은 사인파 신호에 적합하지만 노이즈에 강하지 않습니다. 반면 주파수 도메인 방법은 신호를 주파수 성분으로 분해하여, 주파수 성분에 해당하는 푸리에 계수를 통해 주기도를 생성합니다.

자기상관과 푸리에 변환은 가장 인기 있는 주기성 감지 기술입니다. 자기상관은 짧은 주기와 긴 주기를 감지할 수 있지만, 진짜 주기의 배수가 진짜 주기와 동일한 강도를 가지기 때문에 실제 주기를 식별하는 데 어려움을 겪습니다. 반면 푸리에 변환은 주기도의 많은 거짓 양성 및 낮은 주파수 영역 또는 데이터의 희소성 문제로 인해 긴 주기를 잘 추정하지 못하는 문제를 겪습니다. 일부 방법은 자기상관과 푸리에 변환을 결합합니다.

우리의 방법은 주기 값을 매개변수로 요구하지 않고 데이터셋에서 가장 중요한 주기를 감지할 수 있으며, 이는 시간 도메인에서 이루어집니다. 또한, 우리의 방법은 다양한 유형의 주기성을 감지합니다.

Preliminaries

주기성, 근사 주기성, 문제 정의
정의 1: 길이 n의 시계열 문자열 S = t0, t1, ..., tn-1이 주어졌을 때, S가 주기적이라고 하려면 S(t) = S(t+p)가 성립해야 하며, 여기서 t ∈ N, t ≥ 0, t < n-p, T는 S의 부분 문자열로 T= t0, t1, ..., tp-1, |T| = p, p ≥ 1 그리고 p ≤ n/2입니다. 가장 작은 부분 문자열 T는 S의 주기라고 합니다. 예를 들어, S = wxywxywxy일 때, 주기는 T=wxy, p=3입니다. (길이 (m*p)인 부분 문자열은 m ≠ 1인 경우 주기로 간주하지 않습니다.)

정의 2: 알파벳 Σ 위의 n-길이 문자열 S가 주어졌을 때, r을 문자열에 정의된 오류 함수라고 합니다. 만약 r(S, T) = k인 문자열 T가 존재한다면, S는 T에 대해 k 오류를 가지는 주기적이라고 합니다. 가장 작은 k를 가지는 문자열 T는 S의 근사 주기라고 합니다. 예를 들어, S = wxywxywxy, r(S, A) ≥ r(S, B)에서 A = wxy는 위치 0, 3, 6에서 발생하고 B = wxy는 위치 0, 6에서 발생합니다. A와 B는 후보 주기이며, A가 S의 근사 주기(즉, 가장 중요한 주기)입니다.

---

정의 2번의 개념
정의 2번은 "근사 주기성"을 설명합니다. 이는 데이터가 완벽하게 주기적이지 않지만, 일부 오차를 허용하면서 주기적이라고 볼 수 있는 경우를 의미합니다.

예시
다음의 문자열 S가 있다고 가정해봅시다:
S = "wxywxywxy"

여기서 우리가 찾고자 하는 주기(반복되는 패턴)는 T입니다. 이상적인 경우, S는 "wxy"라는 패턴이 반복된다고 볼 수 있습니다.

그러나 실제 데이터에서는 약간의 오차가 있을 수 있습니다. 예를 들어, 다음과 같은 문자열을 생각해봅시다:
S' = "wxywxzwxy"

이 문자열 S'에서 "wxy"가 반복되지만, 중간에 "wxz"라는 부분이 있습니다. 이런 경우에도 "wxy"가 주기적인 패턴으로 여겨질 수 있습니다.

정의 2번의 설명
기본 문자열 S: "wxywxywxy"

후보 패턴 A와 B:

후보 패턴 A: "wxy", 위치 0, 3, 6에서 발생
후보 패턴 B: "wxy", 위치 0, 6에서 발생
오차 함수 r: 주기 패턴과 문자열 사이의 차이를 평가하는 함수입니다. 예를 들어, "wxywxywxy"와 "wxz"의 차이는 "y"와 "z"의 차이로, 1의 오차가 있을 수 있습니다.

오차 계산:

A의 오차 r(S, A) = 0 (위치 0, 3, 6에서 완벽하게 일치)
B의 오차 r(S, B) > 0 (위치 0, 6에서만 일치)
이 예시에서 패턴 A는 S의 근사 주기(가장 중요한 주기)입니다.

정리
근사 주기성: 문자열 S가 완벽하게 주기적이지 않더라도, 일부 오차를 허용하면서 반복되는 패턴(T)을 찾을 수 있습니다.
가장 중요한 주기: 가장 작은 오차를 가지는 패턴(T)이 근사 주기입니다.

문제 정의: 문자열 함수 r과 알파벳 Σ 위의 길이 n인 문자열 S가 주어졌을 때, 함수 r에 따라 근사 주기 T를 계산합니다.

---

모티프 발견
시계열 모티프는 반복되는 유사한 패턴입니다. 자주 발생하는 패턴을 감지하는 것이 주기성 감지의 전 단계로 유용할 수 있습니다. 많은 알고리즘이 시계열 데이터에서 모티프를 찾기 위해 제안되었습니다. 이 연구에서는 GrammarViz에 초점을 맞추고 있으며, 이는 문법 유도를 기반으로 한 빠르고 근사적인 가변 길이 모티프 발견 알고리즘입니다.

GrammarViz는 시계열의 문자열 표현에서 모티프를 도출하기 위해 Sequitur라는 문맥 자유 문법 유도 기술을 활용합니다. 이 모티프들은 원래 시계열로 매핑되어 그 발생 위치를 보여줍니다. 문자열 표현에서 작동할 수 있는 능력 덕분에 이 기술은 다양한 종류의 데이터에도 적용될 수 있습니다. GrammarViz는 가변 길이 모티프를 효과적이고 효율적으로 감지할 수 있는 최초의 시계열 모티프 발견 알고리즘으로, 스트리밍 방식으로도 작동할 수 있습니다. 또한, GrammarViz는 결과를 명확하게 시각화하고 쉽게 탐색할 수 있는 도구도 제공합니다.

GrammarViz는 수의 감소 덕분에 가변 길이 모티프 발견을 달성하여, 주기적 패턴이 시계열에서 가변 길이로 발생할 수 있는 경우에 적합합니다.

---

GrammarViz는 시계열 데이터에서 모티프(반복되는 패턴)를 발견하기 위한 알고리즘입니다. 이 알고리즘은 주기적인 패턴을 감지하는 데 사용될 수 있으며, 특히 가변 길이의 모티프를 효과적이고 효율적으로 찾는 데 강점이 있습니다. GrammarViz는 두 가지 주요 단계를 통해 작동합니다:

1. 시계열 데이터를 문자열로 변환
   GrammarViz는 시계열 데이터를 Symbolic Aggregate approXimation(SAX)이라는 기법을 사용하여 문자열로 변환합니다. SAX는 시계열 데이터를 이산화(discretize)하여 문자열 형태로 표현합니다. 예를 들어, 원래의 시계열 데이터가 [2.3, 2.5, 3.1, 2.8]이라면, 이를 각각의 값 구간에 따라 문자 'a', 'b', 'c'로 변환할 수 있습니다.

2. 문자열에서 모티프 발견
   GrammarViz는 변환된 문자열에서 모티프를 발견하기 위해 Sequitur라는 문법 유도(Grammar Induction) 알고리즘을 사용합니다. Sequitur는 문자열 내의 반복되는 패턴을 찾아내어 이를 문맥 자유 문법(Context-Free Grammar) 규칙으로 변환합니다.

Sequitur 알고리즘
입력: 변환된 문자열 (예: "abcabcabc")
작업: 반복되는 패턴을 찾아 규칙으로 변환 (예: "abc"가 반복되므로, 이를 규칙으로 정의)
출력: 문법 규칙 세트 (예: "R1 -> abc", "S -> R1R1R1")
GrammarViz의 장점
효율성: 공간 및 시간 면에서 효율적입니다.
가변 길이 모티프 감지: 모티프의 길이가 일정하지 않아도 감지할 수 있습니다.
스트리밍 데이터 처리: 실시간으로 들어오는 데이터에서도 모티프를 감지할 수 있습니다.
다양한 데이터 적용: 문자열로 변환할 수 있는 다양한 종류의 데이터에 적용할 수 있습니다.
사용 예시
GrammarViz는 시계열 데이터를 처리하여 다음과 같은 패턴을 발견할 수 있습니다:

주식 시장 데이터에서 주기적인 가격 변동 패턴 발견
ECG(심전도) 데이터에서 이상 패턴 감지
동물의 이동 패턴 분석
결론
GrammarViz는 시계열 데이터에서 반복되는 패턴을 효과적이고 효율적으로 발견하는 데 유용한 도구로, 이를 통해 주기성을 감지하고 분석하는 데 큰 도움을 줄 수 있습니다.

---

Proposed Method

우리 접근법의 기본 전제는 시계열에서 높은 효율성과 효과성으로 모티프를 먼저 발견한 다음 가장 주기적인 모티프를 감지하는 것입니다. 알고리즘 1은 MBPD 알고리즘의 의사 코드를 보여줍니다. 2번째 줄에서 반환된 모티프 객체는 시계열 내에서 각 발생의 시작 및 종료 위치와 함께 저장됩니다. 우리는 이 작업에서 시계열에서 최소 3번 발생하는 주기만 고려합니다. 그보다 적게 발생하는 주기는 거짓 양성일 확률이 높기 때문입니다. 하지만 필요에 따라 두 번 발생하는 주기를 감지하도록 알고리즘을 수정하는 것은 사소합니다.

3-7번째 줄과 8-14번째 줄의 루프는 각 모티프의 주기와 모든 발생 간격의 표준 편차로 정의된 오류(정의 2의 r 함수) 및 근사 주기를 계산합니다. 각 모티프의 주기는 시계열에서 모든 발생 간격(두 개의 연속된 발생의 시작 위치 사이의 간격)의 평균으로 계산됩니다. 근사 주기와 오류의 계산은 도출된 문자열 모티프가 원래 시계열로 매핑된 후 원래 시계열에서 수행됩니다. 시계열의 근사 주기는 가장 낮은 오류에 해당하는 주기입니다. 알고리즘 1의 4번째 및 9번째 줄에서 호출된 주기성 함수는 알고리즘 2에 나와 있습니다.

MBPD의 효율성은 주로 GrammarViz(2번째 줄)의 효율성에 달려 있으며, 이는 Sequitur를 핵심으로 합니다. GrammarViz는 선형 시간 및 공간 복잡도를 가집니다. 결과적으로 MBPD의 시간 복잡도는 크기가 n인 시계열에 대해 O(n*k)이며, 여기서 k는 Sequitur에 의해 생성된 각 모티프 규칙의 평균 인스턴스 수입니다. 공간 복잡도는 여전히 O(n)인데, 이는 알고리즘 1 및 2에서 사용되는 변수에 필요한 메모리 공간이 무시할 수 있을 정도로 적기 때문입니다. 대부분의 기존 시계열 주기성 감지 방법과 비교할 때, MBPD는 경쟁력 있는 공간 및 시간 복잡도를 가지고 있습니다.

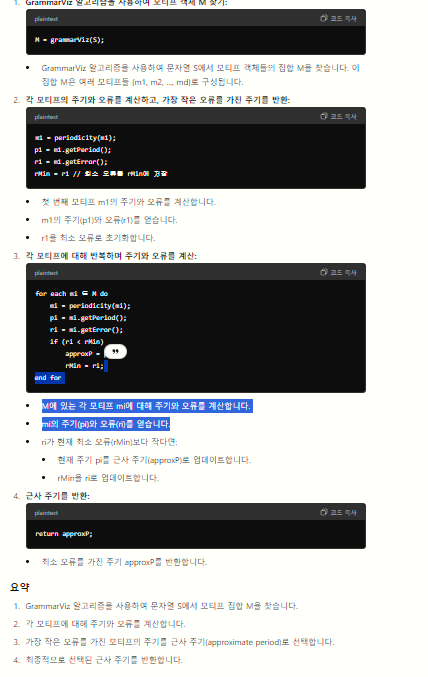
알고리즘 2: 모티프의 주기와 오류 계산
변수 초기화:

sum_Interval = 0, sqd = 0;
간격의 합과 제곱 편차의 합을 초기화합니다.
각 발생 위치 간격의 합 계산:

for each ai ∈ A do
sum_Intervals = sum_Intervals + ai - ai-1;
각 발생 위치 ai에 대해 간격을 계산하여 sum_Intervals에 더합니다.
평균 간격(주기) 계산:

M.period = sum_Intervals/(b-1);
주기를 간격의 합(sum_Intervals)을 (b-1)로 나누어 계산합니다.
각 간격의 제곱 편차 계산:

for each ai ∈ A do
sqd = sqd + ((ai - ai-1 - M.period) ^ 2);
각 간격의 편차를 제곱하여 sqd에 더합니다.
오류(표준 편차) 계산:

M.error = (sqd/(b-1)) ^ 0.5;
제곱 편차의 평균의 제곱근을 구하여 오류를 계산합니다.
주기와 오류가 설정된 모티프 반환:

return M;
주기와 오류가 설정된 모티프를 반환합니다.

5 Experiment

MBPD 평가 요약
이 섹션에서는 MBPD를 합성, 준합성 및 실제 데이터셋에서 평가합니다. 주기성 감지 및 시각화 소프트웨어는 GrammarViz의 확장입니다. 실험은 2.7GHz Intel Core i7, MAC OS X 10.7.5, 8GB 메모리에서 수행되었습니다.

주요 내용:

시각화 도구: ECG 데이터셋에서 감지된 근사 주기성을 보여주는 시각화 도구의 스냅샷이 Fig. 1에 있습니다. 다른 주기들은 시퀀스 문법 섹션에서 탐색할 수 있습니다.
비교 방법: Fast Fourier Transform (FFT)와 비교합니다. FFT는 실수 값 데이터셋에 적합합니다. FFT에서 가장 높은 스펙트럼 파워를 가지는 주파수를 시간 도메인으로 변환하여 가장 중요한 주기로 간주합니다.
다른 방법과의 비교: STNR, WARP, 확률 기반 방법도 고려했으나, 각 방법의 문제로 인해 부적합하다고 판단되었습니다. 예를 들어, WARP는 큰 데이터셋에서 메모리 예외를 발생시켰고, STNR은 많은 후보 주기를 반환하여 우리의 목표와 맞지 않았습니다. 확률 기반 방법은 이진 시퀀스에 적합하여 실수 값 시퀀스에는 적합하지 않았습니다.
데이터셋
총 12개의 데이터셋을 사용:

합성 데이터셋 (6개):

S_ONE: 65636 포인트, 완벽한 세그먼트 주기성 (10000 포인트 반복, 마지막 4364 포인트 제외)
S_TWO: 65636 포인트, 완벽한 세그먼트 주기성 (10000 포인트 반복, 마지막 4364 포인트 제외)
S_THREE: S_ONE에 10%씩 삽입, 삭제, 교체 형태의 노이즈 추가
S_FOUR: S_TWO에 10%씩 삽입, 삭제, 교체 형태의 노이즈 추가
S_FIVE: S_ONE의 일부 반복과 가변 포인트로 구성된 부분 시퀀스 주기성
S_SIX: S_TWO의 일부 반복과 가변 포인트로 구성된 부분 시퀀스 주기성
실제 데이터셋 (5개):

ECG: 4096 포인트의 심전도 데이터
POWER: 16384 포인트의 전력 소비 데이터
MFCC: 262144 포인트의 MFCC (Rufous-collared Sparrow의 새 노래에서 추출된 데이터)
SOLAR: 8192 포인트의 태양 데이터
SUNSPOT: 2048 포인트의 취리히의 태양흑점 데이터
준실제 데이터셋 (1개):

P_REAL: 512 포인트, 북대서양의 해수면 온도 데이터 (1000년 동안 시뮬레이션된 데이터로 10년 이동 평균 스무딩 적용)

6.2 Result

결과 요약
우리 방법(MBPD)과 FFT의 성능을 합성 및 실제 데이터셋에 대해 비교 평가했습니다. 평가 결과는 다음과 같습니다.

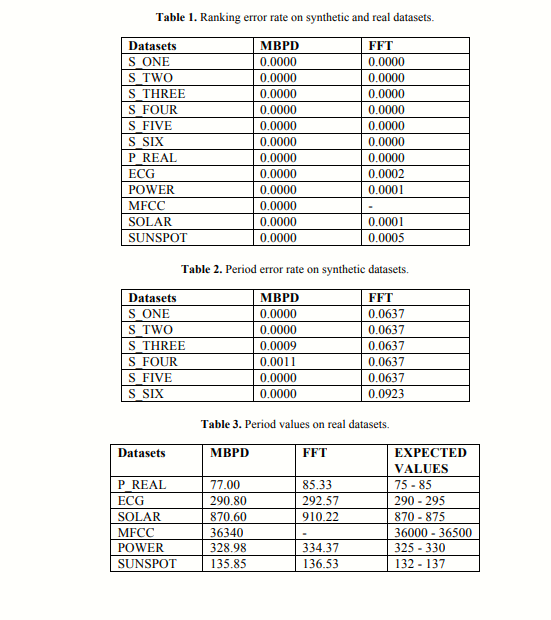
표 1: 합성 및 실제 데이터셋에서 순위 오류율을 비교
표 2: 합성 데이터셋에서 감지된 주기 값의 오류율을 비교

순위 오류율
순위 오류율은 가장 중요한 주기의 순위 위치(i, 0부터 시작)를 시계열의 크기로 나누어 계산합니다. 예를 들어, MBPD가 반환한 후보 주기가 3, 4, 7, 9 순서일 때, 4가 가장 중요한 주기라면 순위 오류율은 1/4 (0.2500)입니다.

주기 값의 오류율
주기 값의 오류율은 다음과 같이 계산됩니다:

주기 값의 오류율

∣
탐지된 주기
−
정확한 주기
∣
정확한 주기
주기 값의 오류율=
정확한 주기
∣탐지된 주기−정확한 주기∣
​

실제 데이터셋
실제 데이터셋의 경우 정확한 주기를 알지 못하기 때문에 주기 값의 오류율을 평가하지 않았습니다. 표 3에는 실제 데이터셋에서 감지된 주기와 예상 범위 값이 포함되어 있습니다. MBPD는 FFT보다 중요한 주기의 순위를 더 잘 매기고 주기를 더 정확하게 감지합니다.

시각화 도구
시각화 도구를 사용하여 결과를 시각화할 수 있습니다. 예를 들어, 그림 1, 3, 4에서 강조된 패턴을 확인할 수 있습니다.

실제 데이터셋의 예상 주기
취리히 태양흑점 데이터: 약 11년(132개월) 주기를 가짐
MFCC 데이터: 새 노래에서 추출된 데이터로, 주기는 약 30K - 40K 사이
표 3에서, 대부분의 실제 데이터셋에서 세 가지 기술 모두 경쟁력 있는 성능을 보였지만, MFCC 추출에서 주기를 감지한 것은 MBPD 뿐이었습니다.

FFT의 문제
MFCC 데이터셋: 10개의 가장 중요한 주기(3.33, 4.00 등)가 모두 예상 주기에서 벗어났습니다.
FFT는 저주파 영역에서의 문제로 인해 긴 주기를 감지하는 데 어려움이 있습니다.
결론적으로, MBPD는 중요한 주기를 더 잘 감지하고 주기를 더 정확하게 찾는 우수한 기술임을 입증했습니다.