Abstract

이미지 검색을 통한 로컬라이제이션은 간단한 매핑 및 매칭 기술로 인해 비용이 저렴하고 확장 가능합니다. 그러나 로컬라이제이션 정확도는 주로 대조 학습을 통해 얻은 기본 이미지 특징의 품질에 따라 달라집니다. 대부분의 대조 학습 전략은 다른 클래스들 사이를 구별하는 특징을 학습합니다. 하지만 로컬라이제이션의 맥락에서는 클래스의 자연스러운 정의가 없습니다. 따라서 선택된 앵커 이미지와의 기하학적 근접성 측정에 따라 이미지가 인위적으로 양성/음성 클래스로 나뉘게 됩니다. 본 논문에서는 이러한 분할이 로컬라이제이션 특징 학습에 왜 문제가 되는지 보여줍니다. 우리는 근접성 측정에 기반한 인위적인 분할이 근접 임계값 근처의 이미지에 대한 본질적으로 모호한 감독 때문에 바람직하지 않다고 주장합니다. 이 문제를 피하기 위해, 우리는 대조 학습을 위해 이미지의 소프트 양성/음성 할당을 사용하는 새로운 기술을 제안합니다. 우리의 소프트 할당은 기하학적 공간과 특징 공간 모두에서 가까운 이미지와 먼 이미지 사이에 점진적인 구분을 만듭니다. 네 가지 대규모 벤치마크 데이터셋에 대한 실험은 검색 기반 시각적 로컬라이제이션을 위한 최첨단 방법보다 우리의 소프트 대조 학습의 우수성을 입증합니다.

1. Introduction

문제 정의: 이미지 검색을 통한 로컬라이제이션은 간단한 매핑 및 매칭 기법으로 인해 비용이 저렴하고 확장성이 좋지만, 이미지의 특징을 학습할 때 인위적으로 양성/음성 클래스로 나누는 방식은 근접 임계값 근처에서 모호한 감독 문제를 야기합니다.

제안된 방법: 이러한 문제를 해결하기 위해, 우리는 이미지의 소프트 양성/음성 할당을 사용하는 새로운 대조 학습 기법을 제안합니다. 이 기법은 기하학적 공간과 특징 공간 모두에서 가까운 이미지와 먼 이미지 사이를 점진적으로 구분합니다.

실험 결과: 네 가지 대규모 벤치마크 데이터셋을 사용한 실험을 통해, 우리의 소프트 대조 학습 방법이 최첨단 방법보다 우수함을 입증합니다.

주요 기여:

로컬라이제이션 특징 학습을 위한 공식적인 이론적 프레임워크를 제안합니다.
제안된 프레임워크 내에서 새로운 손실 함수를 공식화하고, 원래의 다목적 문제를 해결할 수 있는 다른 가능성을 제시합니다.
네 가지 대규모 데이터셋을 사용하여 우리의 방법이 기존 최첨단 방법보다 명확하게 우수함을 입증합니다.

2. Related Work

2.1. Visual localization features

(i) 장소 인식을 위해 학습되고 테스트된 연구 [32, 18, 33]; (ii) 장소 인식을 위해 학습되고 로컬라이제이션을 위해 테스트된 연구 [16, 29, 30]; (iii) 로컬라이제이션을 위해 학습되고 테스트된 연구 [31]. 첫 번째 범주의 방법들은 장소를 인식하는 특징을 학습하도록 설계되었으며, 동일한 설정에서 테스트됩니다. 두 번째 범주는 장소 인식을 목표로 하지만, 시각적 로컬라이제이션 작업에 어느 정도 일반화될 수 있는 방법들을 포함합니다. 세 번째 범주는 로컬라이제이션을 위해 설계되고 테스트된 방법들입니다. 우리의 연구는 세 번째 범주에 속하며, 주로 소프트 할당과 하드 할당의 차이 때문에 [31]과 다릅니다 (1장을 참조하십시오). 자세한 내용은 [34, 35]를 참조하십시오.

2.2. Assignments for contrastive learning

기존의 양성/음성 분리를 위한 할당 기법들은 크게 다음과 같이 나눌 수 있습니다: (i) 하드 할당 [36, 26, 20, 27, 37, 38, 16, 29, 30, 28]; (ii) 하이브리드 할당 [39, 37, 40, 31]; (iii) 소프트 할당 [41]. 하드 할당은 이미지를 엄격히 양성/음성 클래스로 구분합니다 (우리의 경우 앵커와 관련하여). 하이브리드 할당은 또한 이산적인 구분을 사용하지만, 카테고리 내의 샘플에 대해 다른 처리를 허용합니다. 예를 들어, [31]은 특징 거리가 양성 쌍의 기하학적 거리와 비례하도록 특징을 찾습니다. 소프트 할당은 샘플의 이산적인 구분을 사용하지 않습니다. 우리의 연구는 소프트 할당을 수행하지만, 찾고자 하는 특징 공간의 원하는 속성 때문에 [41]과 근본적으로 다릅니다. 특히, [41]은 모든 쌍에 대해 비례적인 특징 및 기하학적 거리를 추구합니다 (양성 쌍에 대해서만 비례성을 적용한 [31]과는 다르게). 우리는 기하학적으로 멀리 떨어진 샘플들에 대해서는 충분히 큰 특징 거리가 있으면 된다고 주장합니다. 모든 쌍에 대해 비례성을 강요하는 것은 기하학적 지도를 암기하는 위험을 초래합니다. 이것이 [31]이 양성 쌍에 대해서만 비례성을 적용하는 이유입니다. 우리의 방법에서는 기하학적 공간에서 가까운 (혹은 먼) 샘플들이 특징 공간에서는 멀리 (혹은 가까이) 있는 경우 앵커 쪽으로 끌어당기거나 (혹은 밀어내는) 방식으로 처리합니다 (그림 1을 참조하십시오). 또한, 우리의 방법이 모든 광범위한 실험에서 [41]보다 성능이 훨씬 뛰어납니다. 대조 학습에 대한 자세한 내용과 최신 발전 사항은 [42]를 참조하십시오.

Problem Formulation and Background

Preliminaries

Learning by hard assignments revisited

이게 뭔소리냐면 아래와 같은 소리입니다.

이미지 검색 기반 로컬라이제이션:

주어진 이미지와 그 이미지가 찍힌 위치를 알고 있을 때, 새로운 이미지가 어디서 찍혔는지 찾아내는 방법이에요.
이 작업을 위해, 이미지들을 특징 벡터라는 숫자들의 집합으로 변환하는 함수 𝜙𝜃를 학습해야 해요. 여기서 𝜃는신경망의 매개변수입니다.

문제 정의:
우리는 주어진 이미지와 그 이미지의 위치 정보를 가지고, 새로운 이미지의 위치를 예측할 수 있도록 학습하고자 합니다.
이미지를 특정한 지리적 근접성에 따라 양성(positive)과 음성(negative)으로 나누는 방식이 사용됩니다.

하드 할당 문제

임의로 선택된 두 임계값 𝜏1와
𝜏2에 따라 이미지들을 양성(가까운 이미지)과 음성(먼 이미지)으로 나눕니다.
예를 들어, 어떤 앵커 이미지 𝑎에 대해, 𝜏1보다 가까운 이미지를 양성으로,
𝜏2보다 먼 이미지를 음성으로 나눕니다.
기존 방법은 양성 이미지의 특징 거리와 음성 이미지의 특징 거리가 일정 마진
𝛼
α를 유지하도록 학습합니다.
하드 할당의 문제점:
𝜏1와 𝜏2 사이에 있는 이미지들은 처리하지 않기 때문에, 이 이미지들의 위치를 정확히 반영하지 못합니다.
두 임계값 𝜏1와 𝜏2가 같아질수록, 마진
𝛼가 0으로 수렴해야 합니다. 즉, 실제로는 이 접근법이 유용하지 않게 됩니다.

Learning by Soft Assignments

기존의 이미지 양성/음성 분류 대신, 우리는 특징 거리와 기하학적 근접성 측정을 사용하여 양성도(positiveness)와 음성도(negativeness) 두 가지 점수를 도출합니다. 이를 각각 𝑠+와 𝑠− 라고 합니다.

아래에서 말하는 문제1이란 : 하학적으로 가까운 이미지가 특징 공간에서도 가깝게 유지되도록 매개변수 𝜃를 학습한다.

영향 함수 𝑔+와 𝑔−

Loss function for gap maximization

전체적으로 말하면 어떤 앵커라는 이미지가 들어왔을 때; 한 배치(i)내에 다른 이미지와 비교하여 양성도와 음성도를 측정한다.(특성벡터를 이용하여 -> 여기 특성벡터가 가깝다면 실제 지리적 위치도 가깝다고 문제1에서 정의하고 정의도 해놨다)
만약 한 앵커와 어떤 이미지가 가까운 이미지라면 그 양성도가 증가할것이고 음성도는 낮아질것이다.
-> 그래서 가까운이미지라면 양성도가 최소화되고 음성도는 최대화가 되도록 학습한다(여기서 G함수가 사용)

Experimental Evaluation

훈련 데이터셋
우리는 세 가지 공개된 실제 데이터셋에서 훈련된 모델을 사용하여 실험을 수행했습니다: ImageNet [44], Pittsburgh (Pitts250k) [45], Oxford RobotCar [46]. Pittsburgh와 Oxford RobotCar 모델은 로컬라이제이션을 위해 훈련되었습니다. ImageNet 모델은 분류를 위해 훈련되었으며, 재훈련 없이 로컬라이제이션을 위해 재사용되었습니다. Pittsburgh와 ImageNet 모델의 경우 [16]에서 공개된 체크포인트를 사용했습니다. Oxford RobotCar의 경우, [46]에서 노이즈가 있는 레이블을 신중하게 제거하여 100만 장 이상의 이미지로 구성된 대규모 훈련 데이터셋을 직접 큐레이팅했습니다. 원래의 Oxford RobotCar 데이터셋은 다소 노이즈가 많기 때문에, 위치 이상치(outlier)를 제거하고 과도하게 노출된 이미지나 덜 노출된 이미지를 제외하여 나쁜 또는 비정형적인 위치를 필터링했습니다. 그 결과, 밤, 눈, 흐림, 해, 구름, 비, 황혼 등 다양한 조건에서 촬영된 100만 장 이상의 이미지가 포함된 훈련 데이터셋이 만들어졌습니다. Figure 2의 첫 번째 그래프는 우리의 Oxford RobotCar 훈련 이미지 위치를 보여줍니다. 재현성을 위해, 포함된 모든 이미지의 목록은 보충 자료에 제공됩니다.

테스트 데이터셋
우리는 네 가지 다른 테스트 세트에서 결과를 보고합니다: 자체 Oxford RobotCar [46] 테스트 세트, Pittsburgh (Pitts250k) [45], RobotCar Seasons (Oxford RobotCar [46]의 하위 세트) 및 CMU Seasons (CMU Visual Localization Dataset [47]의 하위 세트). Oxford RobotCar의 경우, 훈련 지역과 지리적으로 분리된 테스트 지역을 선택했습니다 (Figure 2 참조). Oxford RobotCar 테스트 세트의 기준 이미지 선택은 두 가지 가정에 기반합니다. 첫째, 참조 저장소는 제한적이므로 제한된 수의 기준 이미지만 선택합니다. 둘째, 이미지 검색 기반 로컬라이제이션 시스템을 설계하는 사람은 초기 참조 조건을 제어할 수 있을 가능성이 높기 때문에 가장 쉬운 조건을 기준으로 선택하는 것이 정당화됩니다. 이러한 관점에서, 우리는 흐린 날씨의 참조 시퀀스를 선택했습니다. 이 조건은 햇빛이 강한 시퀀스보다 눈부심이 적고 야간 이미지보다 조명이 좋습니다. 원래의 Pittsburgh 데이터셋은 25만 장의 기준 이미지를 포함하고 있습니다. 더 빠른 테스트를 위해, 우리는 가장 가까운 쿼리에서 100미터 이상 떨어진 모든 기준 이미지를 무시하고 주로 하늘을 보여주는 피치 2의 이미지를 제거했습니다. 남아 있는 이미지들의 위치는 Figure 2에 나와 있습니다. 재현성을 위해, 모든 Oxford RobotCar 및 Pittsburgh 테스트 이미지의 목록은 보충 자료에 포함되어 있습니다. RobotCar Seasons 및 CMU Seasons에 대한 평가를 위해 온라인 장기 시각적 로컬라이제이션 벤치마크 [19]를 사용합니다. Figure 2의 표는 네 가지 다른 테스트 세트에 대한 기준 이미지와 쿼리 이미지의 수를 보여줍니다.

네트워크 아키텍처와 훈련
우리는 마지막 합성곱 층에서 잘린 VGG-16 [14] 네트워크를 사용하고 NetVLAD [16] 층으로 확장하여 [48]에 의해 구현된 대로 네트워크를 초기화합니다. 네트워크는 아직 로컬라이제이션을 위해 재훈련되지 않은 ImageNet [44] 분류 가중치로 초기화됩니다. 차원 축소를 위해 PCA를 화이트닝과 함께 사용합니다. Pittsburgh, Oxford Seasons 및 CMU Seasons의 경우, PCA는 참조 이미지를 사용하여 계산됩니다. 우리의 Oxford RobotCar 테스트 세트의 경우, PCA는 Oxford RobotCar 훈련 세트에서 5000개의 이미지를 사용하여 계산됩니다. 이 논문에서 보고된 모든 결과는 최종 특징 크기 256을 사용합니다 (다른 크기에 대한 결과는 보충 자료를 참조하십시오). 이 크기는 [16]에서 사용된 4096보다 훨씬 작습니다. 이로 인해 온라인 벤치마크 [19]에서 [16]의 Pittsburgh 체크포인트로 얻은 결과가 리더보드의 동일한 방법의 결과와 다른 이유입니다.

모든 모델은 단일 Nvidia GPU에서 훈련됩니다. 우리는 [16]의 훈련 매개변수를 사용하여 학습률을 0.000001로 줄였습니다. 각 훈련 튜플은 1개의 앵커, 12개의 가까운 이웃 이미지 및 12개의 더 먼 이미지를 포함합니다. 이미지는 가장 긴 쪽의 길이가 240px이 되도록 축소됩니다. 작은 이미지 크기를 사용하면 [16]에서 conv5 층까지만 훈련했던 VGG-16을 전체적으로 훈련할 수 있습니다. 우리의 Oxford RobotCar 훈련 세트에는 동일한 위치를 여러 번 방문하지만 모든 위치를 동일한 횟수로 방문하지는 않는 많은 시퀀스가 포함되어 있기 때문에, 하나의 에포크를 표준 주행 경로를 따라 1미터마다 하나의 앵커를 선택한 것으로 정의합니다. 각 앵커 이미지에 대해 반경 r1 내에서 앵커와 최대 30도 차이 나는 가까운 이웃을 샘플링합니다. 더 먼 이미지는 최소 r2 거리 이상 떨어진 곳에서 샘플링합니다. 우리의 방법과 로그 비율 손실의 경우, r1과 r2를 15m로 설정합니다. 다른 모든 방법의 경우, r1을 10m, r2를 25m로 설정합니다 [16, 31, 30]. 우리의 방법과 로그 비율 손실의 경우, 가까운 이웃과 더 먼 이미지를 하나의 텐서로 병합하여 손실 계산 중에 구별하지 않고 처리합니다. 다른 방법의 경우, 가까운 이웃은 양성, 더 먼 이미지는 음성으로 처리합니다. [16]과 유사하게 우리는 마이닝 캐시 크기를 1000으로 설정하여 250단계마다 업데이트되는 하드 네거티브 마이닝을 사용합니다. 모든 음성의 절반은 하드 네거티브로 마이닝됩니다. 음성 간의 다양성을 확보하기 위해, 각 음성은 튜플 내의 다른 모든 음성으로부터 최소 r2 이상 떨어져 있어야 합니다. 훈련은 검증 성능이 더 이상 개선되지 않을 때 중지됩니다. Multi-similarity 손실 [28]과 우리의 방법은 한 에포크 내에, 로그 비율 손실은 두 에포크 내에, 다른 모든 방법은 세 에포크 내에 수렴합니다.

평가 지표
우리는 최상위로 검색된 참조 위치와 쿼리 위치 사이의 거리가 주어진 거리 임계값 d보다 작은 경우 이미지를 정확히 로컬라이즈된 것으로 간주합니다. 특정 테스트 조건에서 정확히 로컬라이즈된 이미지의 비율, 즉 로컬라이제이션 정확도를 보고합니다. CMU Seasons와 RobotCar Seasons의 평가에서는 거리 임계값 외에도 각도 오차 임계값을 사용합니다. 장기 시각적 로컬라이제이션 벤치마크 [19]는 6DOF 구조 기반 자세 추정 방법을 평가하도록 설계되었음을 유의하십시오. 이 논문에서 보고된 모든 방법은 순수 검색 기반 방법입니다. 따라서 방법이 기하학적으로 가장 가까운 참조 이미지를 찾더라도, 해당 참조의 자세가 쿼리 이미지 자세와 너무 다르면 정확히 로컬라이즈된 것으로 간주되지 않을 수 있습니다. 따라서 우리의 평가는 더 높은 임계값 d를 사용하고 순수 검색 기반 방법이 2차 구조 기반 자세 정제 단계 없이 달성할 수 있는 최고 가능한 정확도를 보고합니다. 구조 기반 방법은 종종 작은 임계값에서 더 나은 결과를 얻지만, 검색 기반 방법은 이를 상쇄합니다.

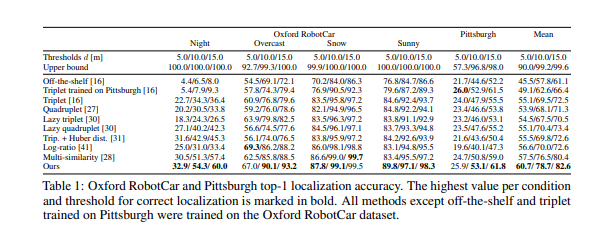
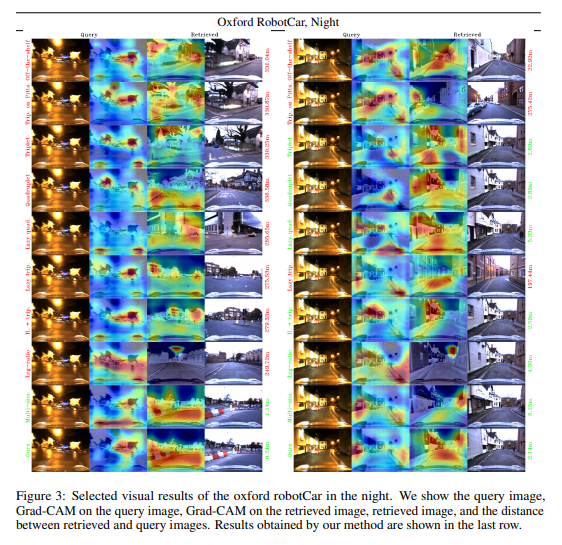
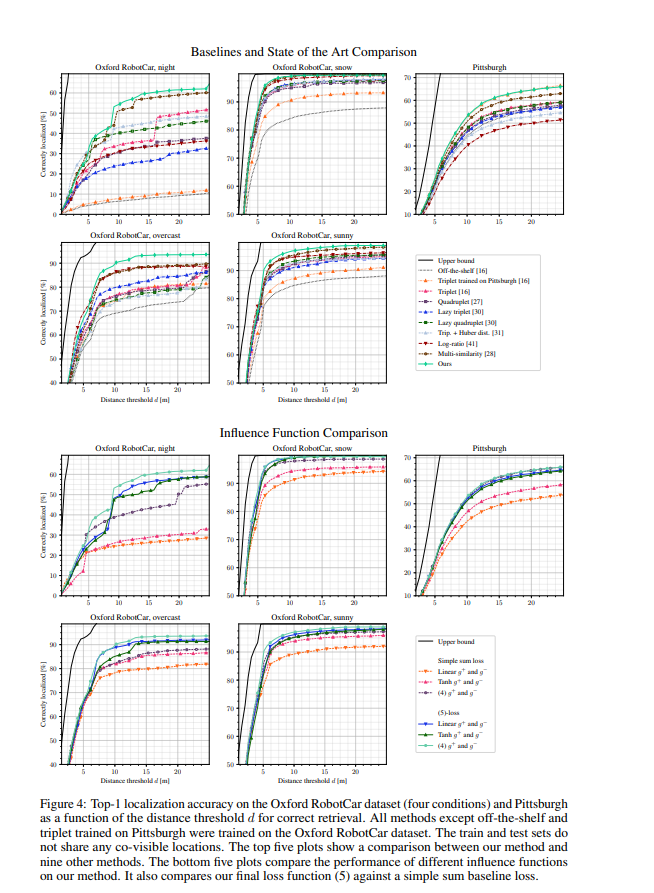
기본값 및 최신 기법 비교

4장에서 소개된 손실 함수를 7가지 다른 기본값과 비교합니다. 이 모든 모델은 Oxford RobotCar 훈련 세트에서 훈련되었습니다. 비교는 로컬라이제이션 맥락에서 이전에 연구된 손실 함수들에 중점을 둡니다: 삼중항 손실 (triplet loss) [16], 네 쌍 손실 (quadruplet loss) [27], lazy 삼중항 및 네 쌍 손실 [30], 그리고 Huber 거리와 함께 사용하는 삼중항 손실 [31]. 또한, 우리의 방법과 유사하게 이진 클래스 레이블을 피하는 log-ratio 손실 [41]과도 비교합니다. 마지막으로, 우리 방법에 영감을 준 부분적으로 현재의 최신 기법인 multi-similarity 손실 [28]과도 비교합니다. Oxford RobotCar에서 훈련된 이 7가지 기본값 외에도, [16]에서 제공된 체크포인트 (off-the-shelf 및 Pittsburgh에서 훈련된 삼중항)로 얻은 결과도 보고합니다. 표 1과 그림 4의 상단은 Oxford RobotCar와 Pittsburgh에서 우리의 평가 설정으로 얻은 기본값과 최신 기법 비교 결과를 보여주며, 표 2는 온라인 벤치마크에서 얻은 RobotCar Seasons 및 CMU Seasons 결과를 보여줍니다. 우리의 방법은 모든 네 가지 테스트 세트에서 가장 뛰어난 성능을 보입니다. (4)에서의 영향 함수 외에도 선형 함수, tanh 함수 및 (5)에 대한 단순 합산 대안 을 테스트했습니다. 그림 4 하단의 다섯 개의 플롯 결과는 (5)와 (4)의 조합이 가장 좋은 성능을 보임을 나타냅니다. 제안된 방법과 비교된 방법들로 얻은 정성적 결과는 그림 3에 나와 있습니다.