Ch 02. 알고리즘을 배우기 위한 준비

알고리즘이란?

개념

• 문제 해결 위한 단계적 절차
• 컴퓨터로 해결 가능
• 입력 존재, 결과(해) 출력

특성

• ㅈㅎㅅ: 입력에 대한 올바른 해
• ㅅㅎㅅ: 각 단계 수행 가능
• ㅇㅎㅅ: 일정 시간 내 종료
• ㅎㅇㅅ: 효율적일수록 가치 상승

표현 방법

• 단계별로
• 말~PL
• 주로 의사코드 사용

분류

• 해결 방식
  • 분할 정복
  • 그리디
  • 동적 계획
  • 근사
  • 백트래킹
  • 분기 한정
    
    
• 문제 기반
  • 정렬
  • 그래프
  • 기하
    
    
• 특정 환경
  • 병렬
  • 분산
  • 양자
    
    
• 기타
  • 유전자 알고리즘 etc.

---

유클리드 호제법

개념

• 최초의 알고리즘

• 최대공약수 알고리즘

  최대공약수: 두 정수 x, y의 약수 중 가장 큰 수
  gcd(x, y)

• 원리

  자연수 x, y(x > y)일 때,
  gcd(x, y) == gcd(y, x - y)

구현

• C

#include <stdio.h>
#define SWAP(a, b){int t; t = a; a = b; b = t;}

int gcd(int x, int y){
	if (x < y) SWAP(x, y);
    
    if(y==0) return x;
    return gcd(y, x % y);
}

• Python

def gcd_recur(x, y):
	if x < y:
    	temp = x
        x = y
        y = temp
    
    if y == 0: return x
    return gcd(y, x % y)
    

def gcd_iter(x, y):
    while y:
    	if x < y:
          temp = x
          x = y
          y = temp
    
    	temp = x % y
        x = y
        y = temp
    
    return x

최대 숫자 찾기

개념

• 카드 하나씩 비교하면서 가장 큰 숫자 기억

구현

• Pseudo code

  //배열 A에 10개 숫자 있을 때(A[10])
  max = A[0]
  for i = 1 to 9
  if (A[i] > max) max = A[i]
  return max

• C

  #include<stdio.h>
  
  int find_max(int A[], int n){
  	int i, max = A[0];
    for(i = 0; i < n; i++)
    	if(A[i] > max)
        	max = A[i];
    return max;
  }

---

알고리즘의 효율성

필요성

• 효율적 알고리즘은 슈퍼컴퓨터보다 더 큰 가치, 더 경제적

공간복잡도

• 알고리즘 수행 시 사용되는 메모리 공간 크기

시간복잡도

• 알고리즘 수행 시 사용된 연산 횟수를 입력 크기 함수로 나타냄
• 점근적 표기(O, Θ, Ω)
  : n → +∞, 복잡도 간단히 표현
• e.g. n장 카드 최대 숫자 찾기
  • n-1 번 비교, 시간복잡도 n-1

최악(big-O, O(n))

• 상한
• 주로 사용하는 방법

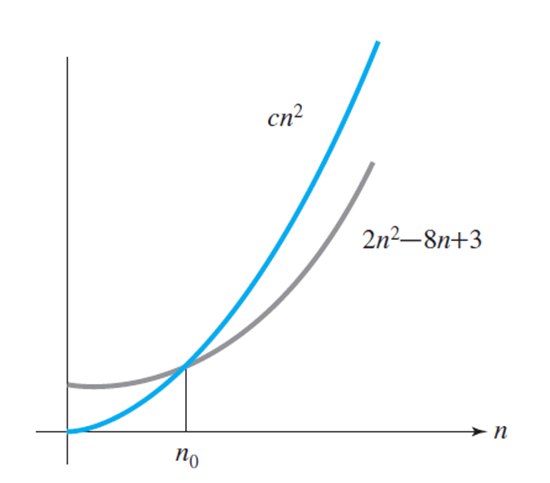
e.g. f(n) = 2n^2 - 8n + 3

• 두 그래프의 교차점 이후 f(n)은 cn^2보다 절대로 커질 수 없다.
• n 증가함에 따라 cn^2은 f(n)의 상한이 된다.
• 따라서 O(n^2)은 f(n)의 점근적 상한
  

• 표기 예
  • n>=2, 3n + 2 <= 4n → O(n)
  • n>=2, 3n + 3 <= 3n^2 → O(n^2)

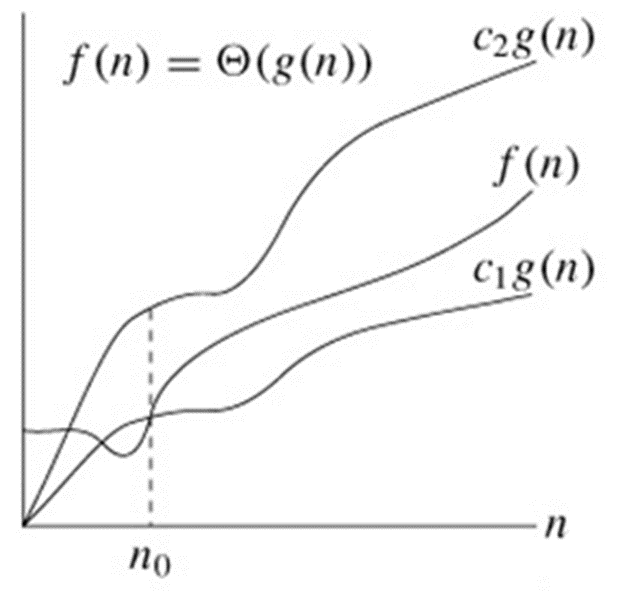
평균(big-Theta, Θ(n))

• 동일한 증가율(상한과 하한 사이)

• n0 이후 모든 n에 대해 c1g(n), c2g(n) 모두 상한, 하한을 동시에 만족한다.
• 따라서 Θ(g(n))
  

• 표기 예
  • n >=2,
    3n <= 3n + 2 <= 4n → Θ(n)

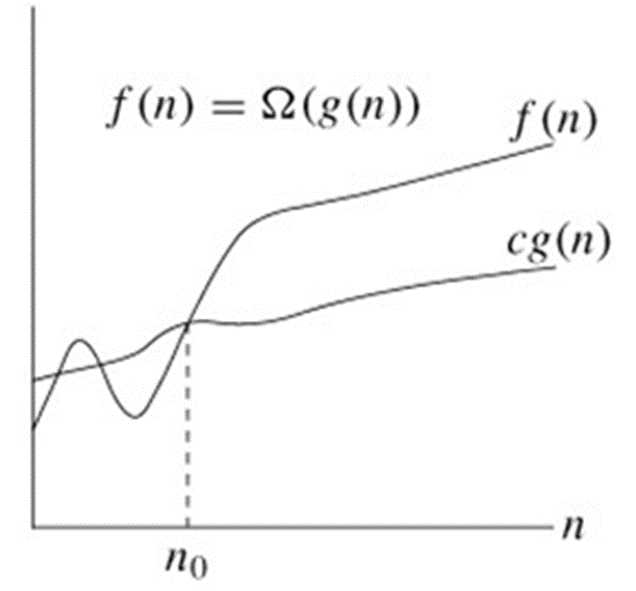
최선(big-Omega, Ω(n))

• 하한

• 교차점 이후 cg(n)은 f(n)에 대해 항상 작다.
  따라서 n 증가함에 따라 cg(n)은 f(n)의 하한이 된다.
  따라서 Ω(g(n))은 f(n)의 점근적 하한
  

• 표기 예
  • n>=2, 3n + 2 >= 4n → Ω(n)

상각

• 분할 상환

---

big-O

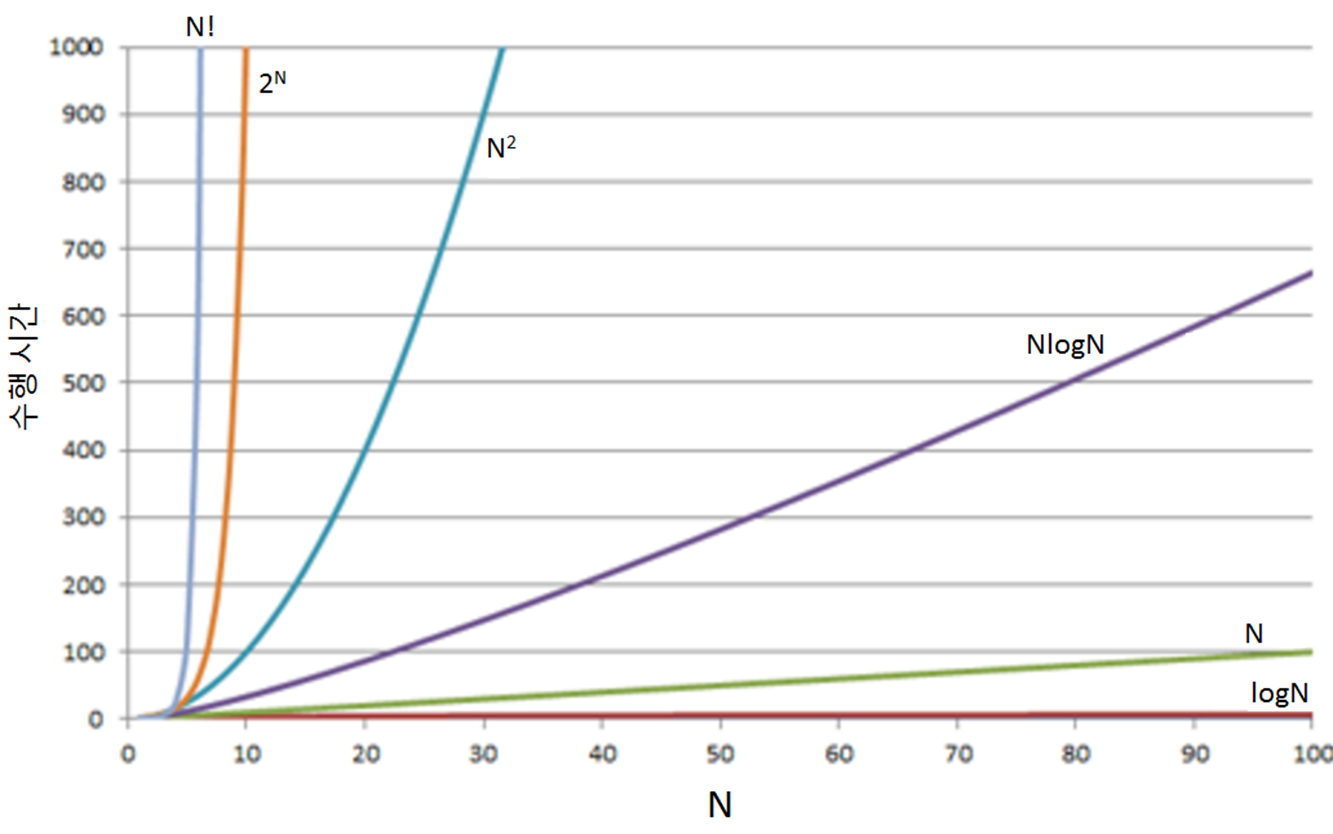
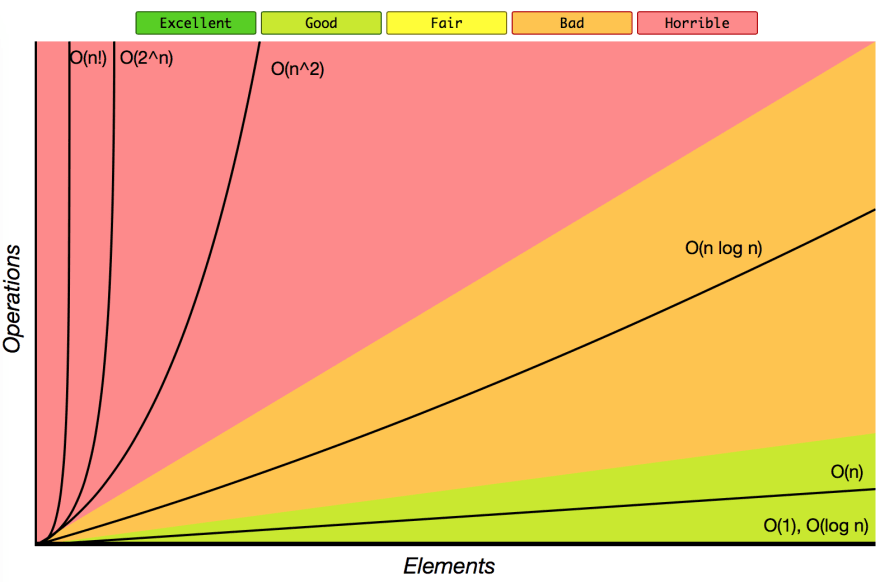
성능비교

1. O(1) – 상수 시간 : 한 단계만 처리
   • e.g. 배열 읽기, 배열 끝 삽입/삭제
2. O(log n) – 로그 시간 : 단계들이 연산마다 특정 요인에 의해 줄어듦
   • e.g. 이진탐색
3. O(n) – 선형 시간 : 단계의 수와 입력값 n이 1:1 선형 관계
   • e.g. 배열 선형 검색
4. O(n log n) - 로그 선형 시간
5. O(n^2) – 제곱 시간 : 단계의 수 = 입력값 n의 제곱
6. O(n^3) – 세제곱 시간
7. O(C^2) - 지수 시간: 상수 C의 n제곱
8. O(n!) - 팩토리얼 시간

성능(오른쪽으로 갈수록 시간 오래 걸림 = 성능 저하)
1 < 2 < 3 < 4 < 5 < 6 < 7 < 8

• 스터디 추가자료