분할 정복 알고리즘이란?
개념
- 분할한 입력 -> 동일 알고리즘 적용 -> 해 계산 -> 취합
- 부분문제: 분할된 입력에 대한 문제
- 부분해: 부분문제의 해
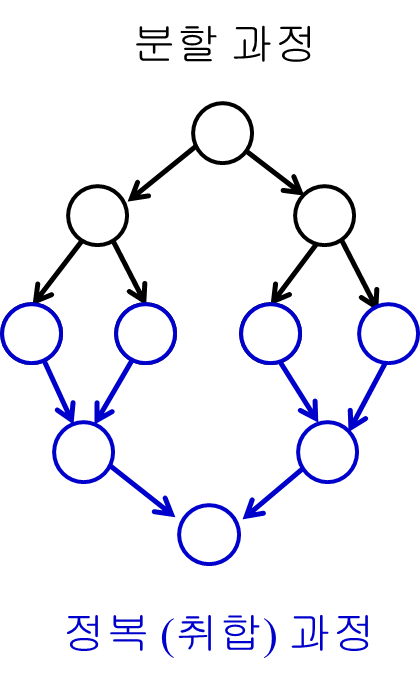
과정
- 분할
- 정복(분할 가능 상태일 경우 '분할'로 돌아감)
- 결합
입력크기 n일 때,
총 분할 횟수k =log n
종류
- 부분문제 수 a, 부분문제 크기 b에 따라 분류
1. a개로 분할, 1/b로 감소
- a=b=2: 합병 정렬, 최근 접점의 쌍 찾기
- a=3, b=2: 큰 정수의 곱셈
- a=4, b=2: 큰 정수의 곱셈
- a=7, b=2: 스트라센의 행렬 곱셈 알고리즘
2. a=2, b=일정 X 감소
- 퀵 정렬
3. a=2(2개 중 하나는 무시), 1/2로 감소
- 이진탐색
4. a=2(2개 중 하나는 무시), b=일정 X 감소
- 선택 문제 알고리즘
5. b=1, 2개씩 감소
- 삽입 정렬, 피보나치 수
합병 정렬
개념
- 부분문제 수: 2개
- 부분문제 크기: 1/2씩 감소
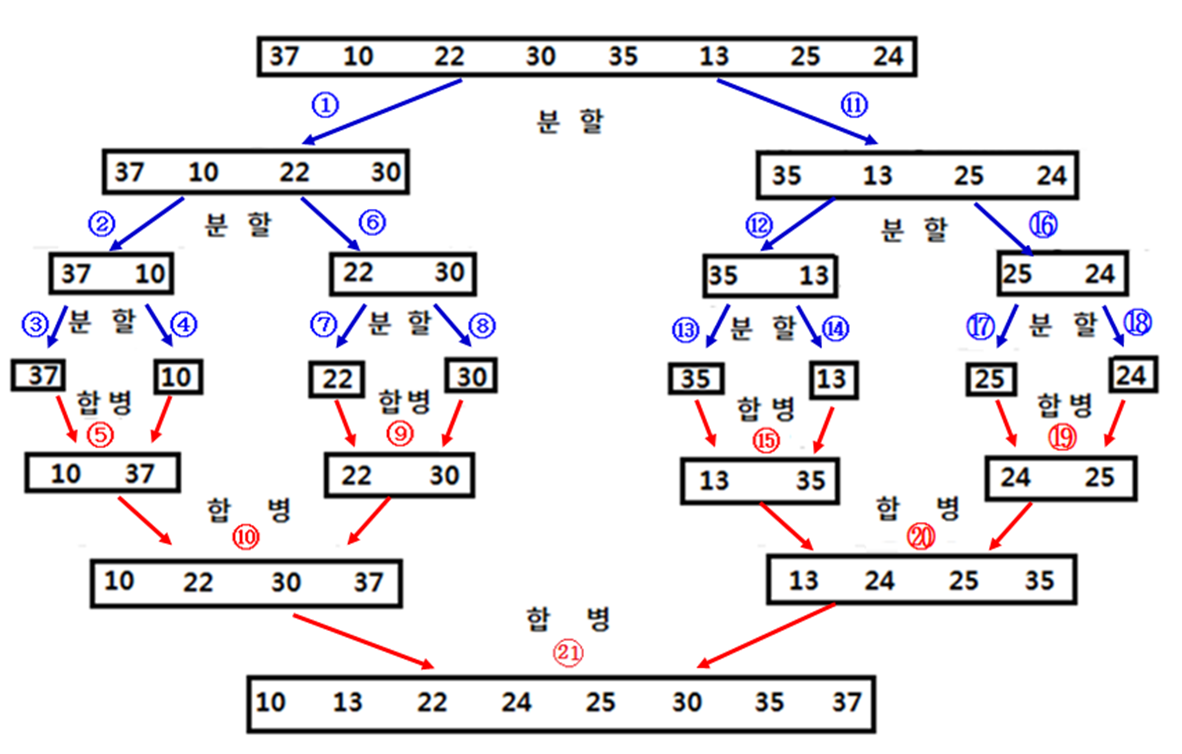
방법
- 분할: 입력 n개 -> n/2 부분 배열 분할(1개 될 때까지)
- 정복: 부분 배열 정렬
- 결합: 부분 배열을 하나로 합병
구현
- 분할
- 배열 원소 수 2개 이상일 때(1개일 때까지) 반으로 나눈다.
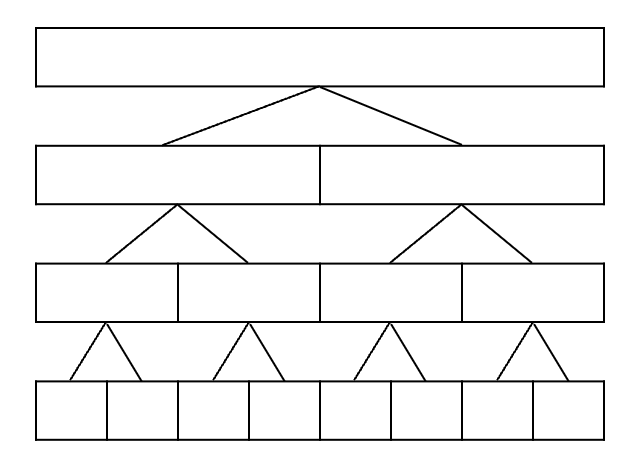
- 배열 원소 수 2개 이상일 때(1개일 때까지) 반으로 나눈다.
- 합병 정렬
- 파이프 앞에서 원소를 하나씩 빼서 비교한 후, 새 파이프에 정리한다는 느낌으로 정렬된 부분 배열을 합병한다.
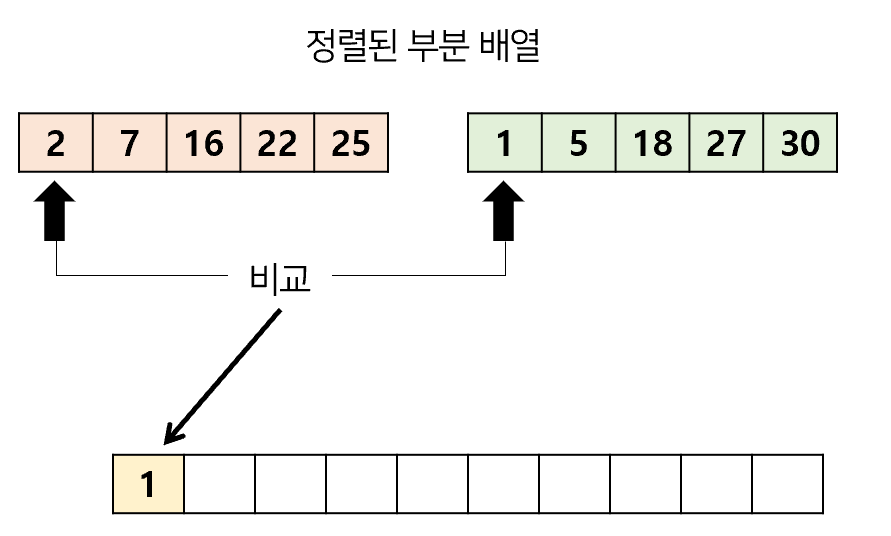
- 파이프 앞에서 원소를 하나씩 빼서 비교한 후, 새 파이프에 정리한다는 느낌으로 정렬된 부분 배열을 합병한다.
Pseudo-codeMergeSort(A, p, q): #배열 A, 첫 인덱스 p, 끝 인덱스 q if p < q: #배열 내 원소가 2개 이상일 때 k = (p + q) // 2 #절반 위치 인덱스(몫만 취함) MergeSort(A, p, k) #앞부분 순환 호출 MergeSort(A, k + 1, q) # 뒷부분 순환 호출 Merge(A, p, q) #부분 배열 합병 정렬
시간복잡도
- 배열 크기 n, 분할 트리를 포화이진트리라고 생각할 때,
분할 시간복잡도: O(1)
합병 횟수: log n
레벨 별 비교 정렬 횟수: n
따라서, 합병정렬 시간복잡도:O(nlogn)
공간복잡도
- 합병 결과 저장할 임시배열 필요:
O(n)
특징/장점
- 안정적 정렬: 순서 변하지 않음
- 연결리스트 정렬 시 효율적
단점
- O(n)의 공간복잡도
응용
- 외부정렬
- 연결리스트 정렬 시
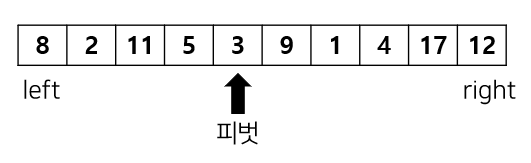
퀵 정렬
개념
- 부분문제 수: 2개
- 부분문제 크기: 불규칙적(일정 X)
방법
- 피벗 정하기
- 피벗보다 작은 숫자들은 왼편, 큰 숫자는 오른편으로 분할(피벗 기준)
- 왼편/오른편(부분문제)에 대해 각각 동일 과정 재귀적 수행
구현
1. 배열에 원소 2개 이상 있을 경우,
1-1. 배열 A[left] ~ A[right] 중 피벗 선택
1-2. SWAP(A[left], 피벗);
1-3. 피벗보다 작은 숫자들은 왼편, 큰 숫자는 오른편으로 옮기기
2. 피벗보다 작은 그룹 1번 과정 순환
3. 피벗보다 큰 그룹 1번 과정 순환
-
Pythondef quick_sort(arr, start, end): if start >= end: return pivot = arr[start] # 피벗은 첫번째 원소 l, r = start + 1, end while l <= r: while l <= end and arr[l] <= arr[pivot]: l += 1 while r > start and arr[r] >= arr[pivot]: r -= 1 if l > r: arr[r], arr[pivot] = arr[pivot], arr[r] else: arr[r], arr[l] = arr[l], arr[r] quick_sort(arr, start, r - 1) quick_sort(arr, r + 1, end) A = [5, 3, 8, 4, 9, 1, 6, 2, 7, 10] print(quick_sort(A, 0, len(A)))
시간복잡도
- 최악:
O(n^2)- 피벗이최소/최대숫자일 경우 - 최선:
O(nlog n)- 분할이 절반으로 이루어질 때(=합병 정렬) - 평균:
O(nlog n)
피벗 선정 방법
퀵 정렬의 성능은 피벗이 좌우!
- 랜덤 선정
- 세 값의 median
pivot = median{K[l], K[(l+r)/2], K[r]}
성능 향상 방법
- 입력 크기 매우 클 때, 삽입 정렬 동시 사용
- 부분 문제 크기 일정 개수 이하: 삽입 정렬 사용
응용/장점
- 입력 크기 클 때 좋은 성능
- 평균 성능이 좋은 정렬 알고리즘
- 유전자 찾는 분야에 접미 배열과 같이 활용
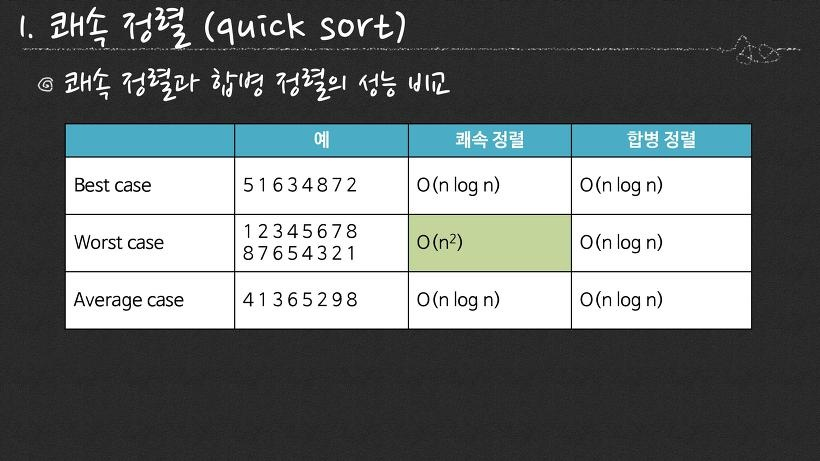
+ 시간복잡도: 합병 정렬 VS 퀵 정렬
.png)