Ch 03. 분할 정복 알고리즘 (2)

선택 문제

문제

• n 개 숫자 중 k번째로 작은 숫자 찾기

원시적 아이디어

• 최소 숫자 k 번 찾기 => O(kn)
• 오름차순 정렬 후 k번째 숫자 찾기 => O(nlogn) (힙 정렬)

선택문제 알고리즘 아이디어

• 이진탐색 알고리즘 이용!
• 그러나 이진탐색과는 다르게 정렬되어 있지 않은 배열

  1. 랜덤 피봇 선택, 퀵 정렬처럼 피봇 기준 Small/Large 그룹 나누기
     • 그룹의 크기 = 그룹 내 숫자 개수 알아야 함
     • Small group 크기: S
     • Large group 크기: L
     • k 번째 작은 숫자
       
       
  2. k가 어느 그룹에 속하는지 알기
     • k <= S: Small group에서 k번째 작은 숫자 찾기
     • k > S+1: Large group에서 k-S-1번째로 작은 숫자 찾기
     • k=S+1: 피봇이 찾던 숫자!(k번째 작은 숫자 = 피봇)
       
       
  3. 찾을 때까지 1, 2번을 재귀적으로 반복

과정

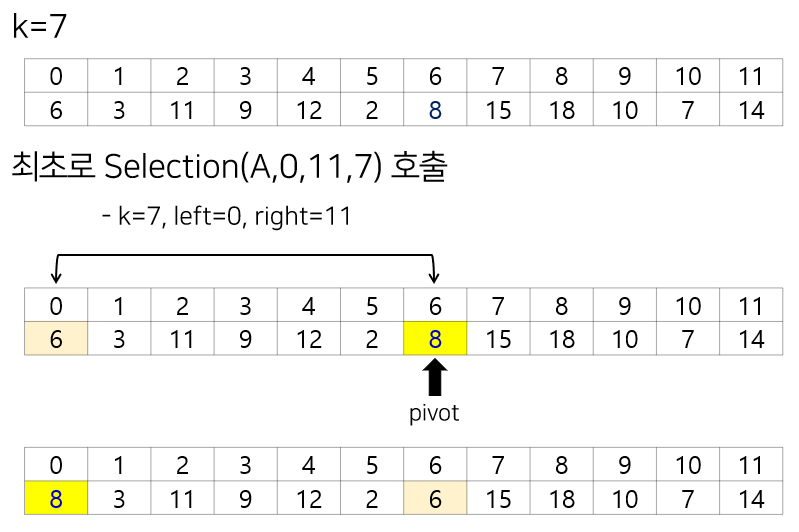
• 퀵 정렬처럼 피봇 기준 Small group과 Large group으로 partition
  
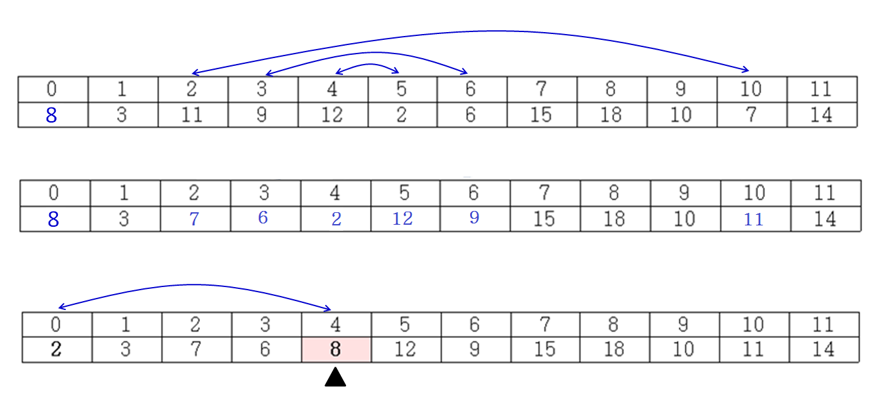
• Small group 크기 S
  • S = (pivot - 1) - left + 1 = 4
  • k = 7이므로, k > S+1
• Large group에서 $k - S - 1 = 2$, 2번째로 작은 수 찾기
  
• 퀵 정렬처럼 피봇 기준 Small group과 Large group으로 partition
  
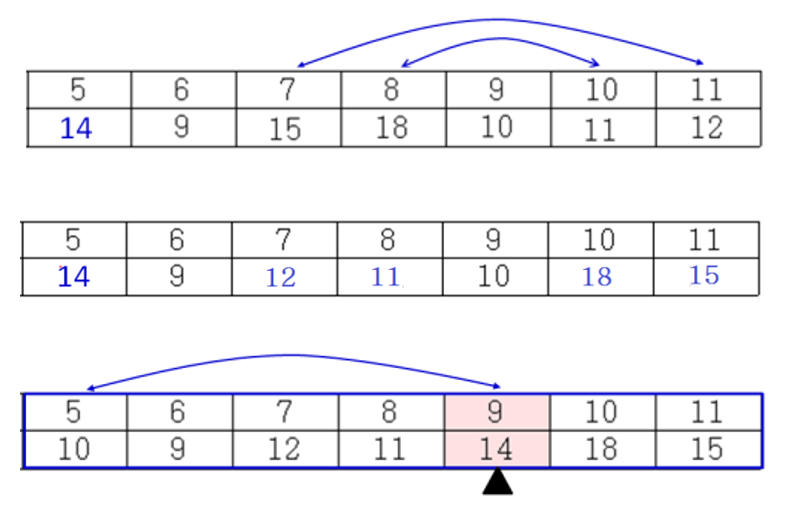
• Small group 크기 S
  • S = (pivot - 1) - left + 1 = 4
  • k = 2이므로, k <= S
• Small group에서 2번째로 작은 수 찾기
• 퀵 정렬처럼 피봇 기준 Small group과 Large group으로 partition
  
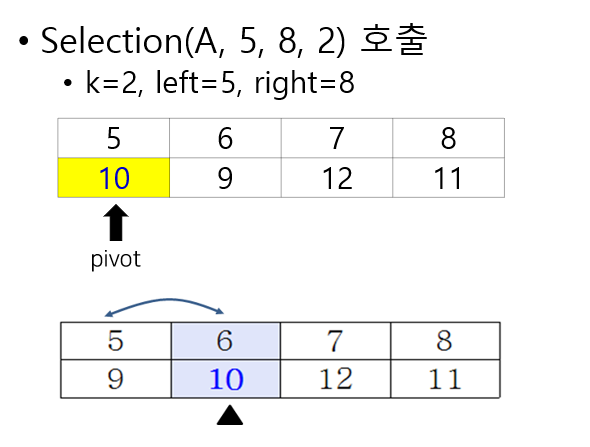
• Small group 크기 S
  • S = (pivot - 1) - left + 1 = 1
  • k = 2이므로, k = S+1 = pivot
• A[6] = 10을 k=7번째 작은 수로 리턴

구현

• Pseudocode

  Selection(A, left, right, k){
      랜덤 피봇 선정;
      퀵 정렬;
      p = pivot;
      S = (p-1) - left + 1;
      if (k <= S) Selection(A, left, p-1, k);
      else if (k == S+1) return A[p];
      else Selection(A, p+1, right, k-S-1);
  }

특징

• 2개의 부분문제로 분할
• 분할된 부분문제 중 하나는 무시 가능
• 부분문제의 크기는 일정하지 않게 감소
• 부분문제 취합 과정 별도로 필요치 않음
• 분할정복 알고리즘이면서 랜덤 알고리즘
  • 피봇 랜덤 설정 → 피봇을 어떻게 설정해야 좋을까?

피봇 선정

• 문제점
  • 피봇이 그룹을 치우치게 분할할 경우 알고리즘 수행 시간 길어짐
• 따라서, 한 그룹 크기가 $(3/4)n$ 넘지 않도록 분할
  • good 분할: 3/4 미만인 경우
  • bad 분할: 3/4 이상인 경우

시간복잡도

• good 분할 / bad 분할 피봇 선택 확률 각각 $1\over2$
• $O(n)$

---

최근접 점의 쌍 찾기

문제

• 거리가 가장 가까운 한 쌍의 점 찾기

원시적 아이디어

• 각각의 두 점 사이의 거리를 계산하기
• $_{n}\mathrm{C}_{2} = {n(n-1)\over 2}$
• 시간복잡도: $O(n^2)$

분할 정복 이용 아이디어

1. $n$ 개의 점을 $1\over2$로 분할하여 각 부분문제에서 최근접 점 쌍 찾기
2. 2개의 부분해 중에서 짧은 거리($=d$) 쌍 찾기
3. 중간영역에서 최근접 점 쌍 있는지 확인
   • L 부분문제 최우측 점$-d$ ~ R 부분문제 최좌측 점$+d$
4. d와 중간영역 최소 거리 중에 최솟값 반환

과정

• S -> S(L)-1, S(R)-1로 분할
  
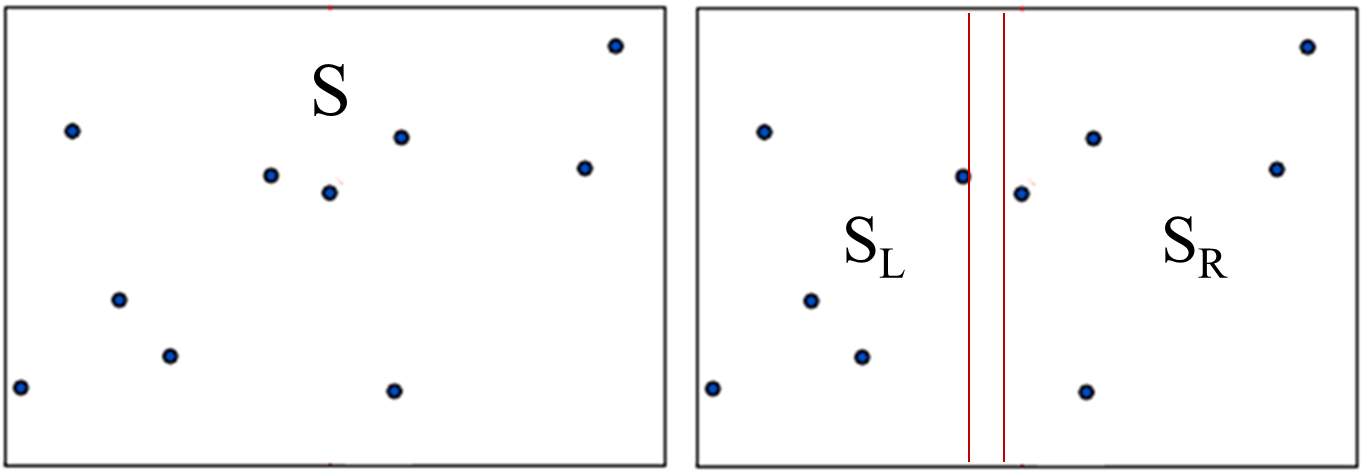
• S(L)-1을 다시 S(L)-2과 S(R)-2로 분할
  
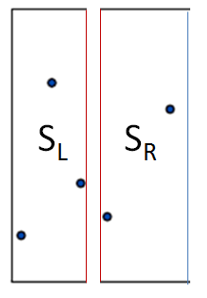
• S(L)-2의 점 3개이므로, 최근접 점 쌍 거리 리턴(20)
  
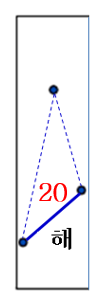
• S(R)-2의 점 2개이므로, 최근접 점 쌍 거리 리턴(25)
  
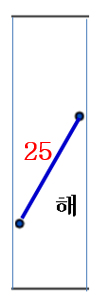
• CP(L)=20, CP(R)=25이므로 $d = 20$
• 중간영역 $\pm d = \pm20$,
  • (S(L) 최우측 - 20) ~ (S(R) 최좌측 + 20)
  • CP(C) 찾기, CP(C) = 10
    
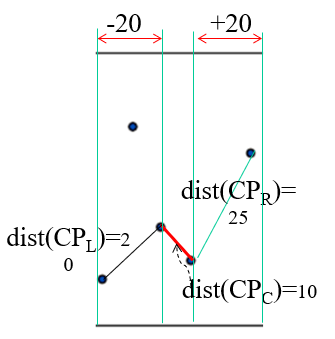
• CP(C) = 10이 최소이므로 10 리턴
• S(R)-1에서도 똑같이 실행, 15 리턴
• 최종, CP(L) -> 10, CP(R) -> 15, CP(R) -> 5
  $\therefore CP(C) = 5$, 최근접 점의 쌍

구현

• Pseudocode

  ClosestPair(S){
      if (i <= 3) return 최근접 점 쌍 거리;
      SL과 SR로 분할;
      CPL = ClosestPair(SL);
      CPR = ClosestPair(SR);

      d = min{dist(CPL), dist(CPR)};
      CPC = 중간영역 최근접 점 쌍의 거리;

      return min{d, dist(CPC)};
  }

시간복잡도

• 입력 시 x-좌표 오름차순 정렬: $O(nlogn)$
• 분할 시: $O(1)$
• 합병 시
  • 각 층에서 중간영역 y-좌표 정렬 * 병합 층수
  • $O(nlogn) * O(logn) = O(nlog^2n)$

$\therefore O(nlog^2n)$

---

분할 정복 적용 시 주의할 점

부적절한 경우

• 입력이 분할될 때마다 부분문제 입력 크기 합이 매우 커지는 경우
  • e.g. 피보나치 수