9.3 유전자 알고리즘
유전자 알고리즘이란?
- 적당히 좋은 해들의 집합(여러 개의 해)에서 출발, 적자생존의 개념으로 최적화 문제를 해결
- 현재 세대의 해로부터 다음 세대의 해를 생성해가며 마지막 세대에서 가장 우수한 해를 반환
후보해
- 후보해
- 각 세대에서의 해들
- 최적해 또는 최적해에 근접한 해가 될 수 있으므로
후보해
- 후보해의 평가
- 후보해의 값 계산
- = 후보해의
적합도
- 우수한 해
- 후보해 중, 최적해의 값에 근접한 적합도를 가진 후보해
후보해 생성 연산
-
선택 연산
- 현재 세대의 후보해 중, 우수한 후보해 선택
- 선택된 후보해의 수는 n개(여러 개)로 유지
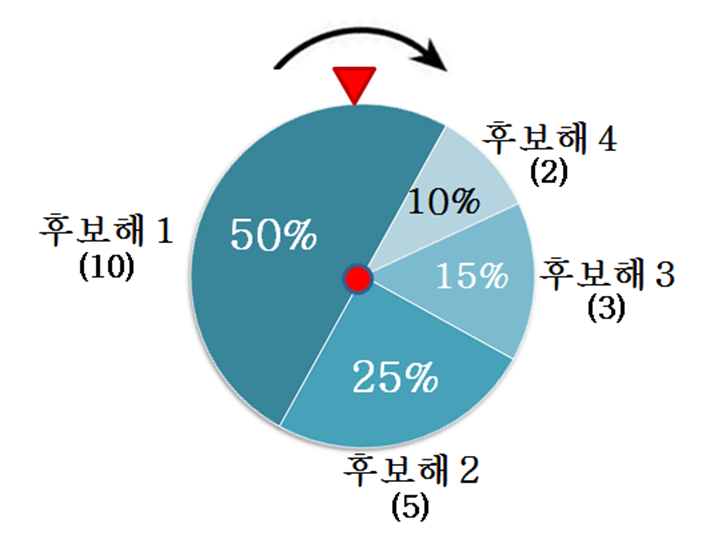
룰렛 휠방법으로 구현- 후보해 개수(n개)만큼 원반 돌리고 선택
- 면적이 넓은 후보해 선택 확률 ↑
- 원반 면적 = (후보해 적합도 / 모든 후보해 적합도 합)에 비례
-
교차 연산
-
선택 연산 수행 후의 후보해에서 수행 -
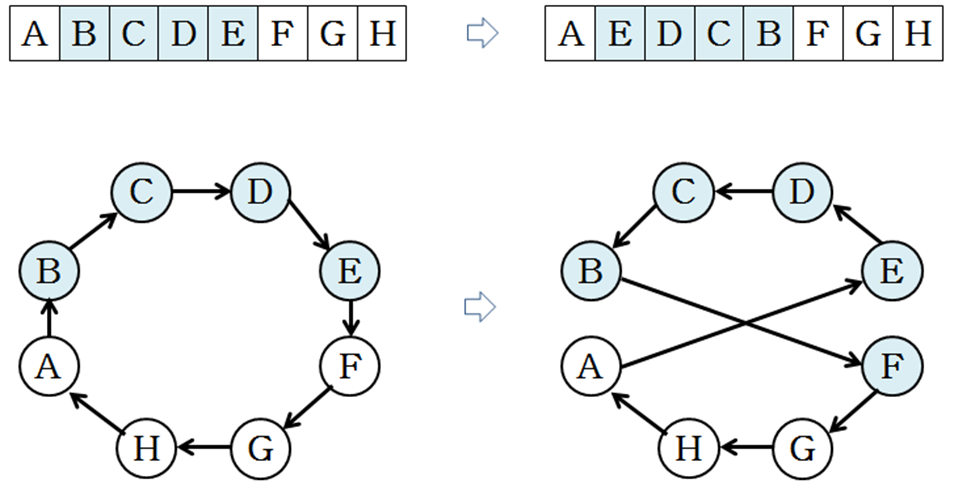
교차점을 선택해 교차점 이후 부분을 서로 교환
- 1-점 교차, 2-점 교차, ...
- 1-점 교차 연산
- 2-점 교차 연산

- 사이클 교차 연산
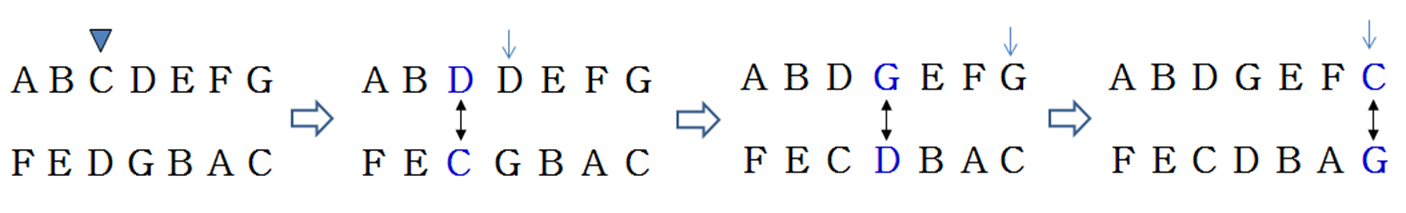
- 1-점 교차 연산
- 1-점 교차, 2-점 교차, ...
-
교차율- 교차 연산을 수행할 후보해의 수
- 0.2~1.0
-
목적: 선택 연산을 통해 얻은 해보다 우수한 후보해 생성
-
-
돌연변이 연산
-
교차 연산 수행 후의 후보해에서 수행 -
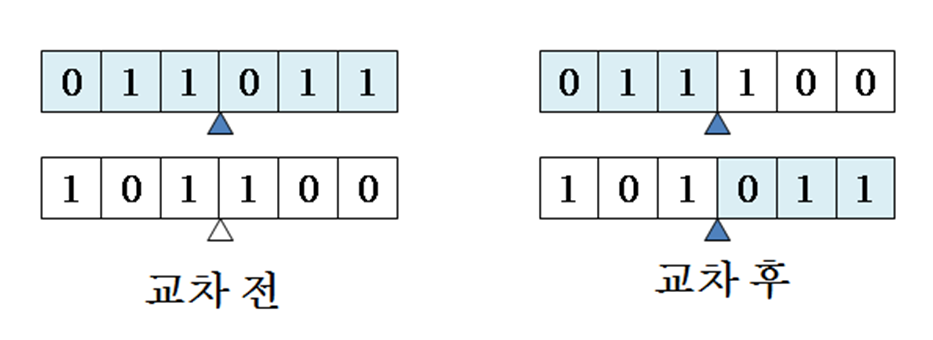
아주 작은 확률로 후보해의 일부분을 임의로 변형
두 번째 bit가 0에서 1로 돌연변이
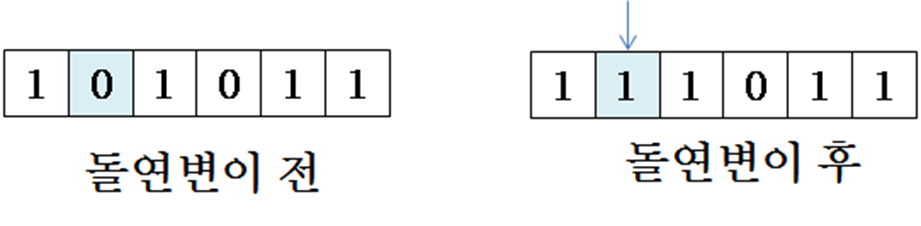
-
돌연변이율- 아주 작은 확률
- (1/한 세대의 후보해의 수) ~ (1/이진 표현 bit 수)의 범위
-
돌연변이 연산이 수행된 후에 후보해의 적합도가 오히려 나빠질 수도 있다.
-
목적: 다음 세대에 돌연변이가 이루어진 후보해와 다른 후보해를 교차 연산함으로써 이후 세대에서 매우 우수한 후보해 생성
-
종료 조건
- 항상 최적해 찾는다는 보장 X → 종료 조건 일정 X
- 일반적으로 더 이상 우수한 해가 출현하지 않으면 알고리즘 종료
특징
- 많은 실험 요구
- 다양한 실험을 통해 종료 조건과 모집단 크기, 교차율, 돌연변이율 등 파라미터의 조절 필요
- 어떤 연산이 주어진 문제에 적절한지도 실험을 통해 결정
- 최적해를 알 수 없고 해결하기 어려운 경우, 최적해에 가까운 해를 찾는 데 적절한 알고리즘
- 항상 최적해 찾는다는 보장 X
- 그러나 대부분 매우 우수한 해 찾음
활용
- NP-완전 문제 해결
- 최적화 문제 해결
9.4 모의 담금질 기법
모의 담금질 기법이란?
- 높은 온도에서 액체 상태인 물질이 온도가 점차 낮아지면서 결정체로 변하는 과정 모방
- 점점 더 규칙적인 방식으로 해 탐색이 이루어진다.
- 항상 전역 최적해를 찾는다는 보장 X
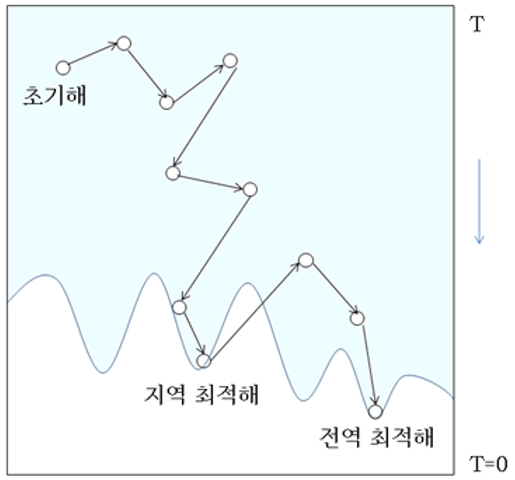
하나의 초기 해로부터 탐색 시작
- 이웃해
- 각 점 : 후보해
- 위쪽 해 < 아래쪽 해(더 우수)
- 후보해 사이 화살표: 이웃하는 관계
확률 개념도입
- 현재 해의 이웃해 중에서 현재 해보다
나쁜해로(위 방향으로) 이동 가능- T ↓, 위쪽으로 이동할 확률 ↓
- 처음 도착한 골짜기(지역 최적해)에서 더 이상 아래로 탐색할 수 없는 상태에 이르렀을 때 ‘운 좋게’ 위 방향으로 탐색하다가 전역 최적해를 찾은 경우
과정
- 임의의 해 s를 선택하여 탐색 시작(충분히 높은 값의 T)
현재 해인 s에이웃하는 해중에서 임의로 s'를 선택- d(= s' - s) 계산
- d < 0 (s' < s):
이웃해가 더 우수한 경우- 현재 해 s 갱신
- d >= 0:
이웃해가 더 나쁘거나 같은 경우q(0∼1 중 랜덤 선택한 수) < p(자유탐색 확률)- 현재 해 s 갱신
- d < 0 (s' < s):
- T를
a(냉각율)만큼 감소 - 종료
- 더 이상 우수한 해를 찾지 못하거나, 미리 정한 최대 반복 횟수 초과 시
- 현재 해 s 리턴
특징
- T가 높을 때부터 점점 낮아지는 것을 확률 p에 반영
- 초기에는 탐색이 자유롭다가 점점 규칙적이 되도록
확률 p- T 기준
T ↑, p ↑=> 자유 탐색T=0, p=0=> 나쁜 이웃해 s'가 s가 되지 못하도록
- d(=s'-s) 기준
d ↑, p ↓d ↓, p ↑- 값의 차이가 큼에도 불구하고 p를 크게 하면 그 동안 탐색한 결과가 무시되어 랜덤하게 탐색하는 결과를 낳기 때문
T: 큰 값 ~ 0d: s'-s
- T 기준
이웃해 정의
- 삽입
- 2개 도시 랜덤 선택
- 두 번째 도시를 첫 번째 도시 옆으로 끼워 넣기
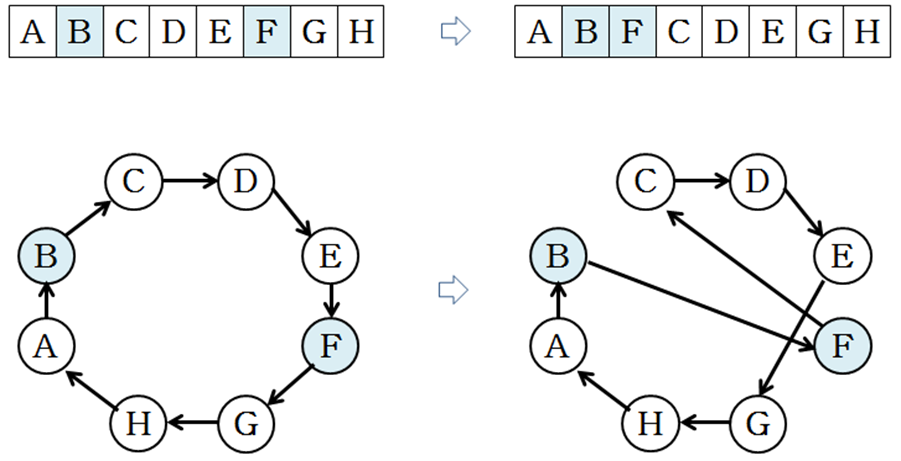
-
교환
- 2개 도시 랜덤 선택
- 도시 위치 서로 바꿈
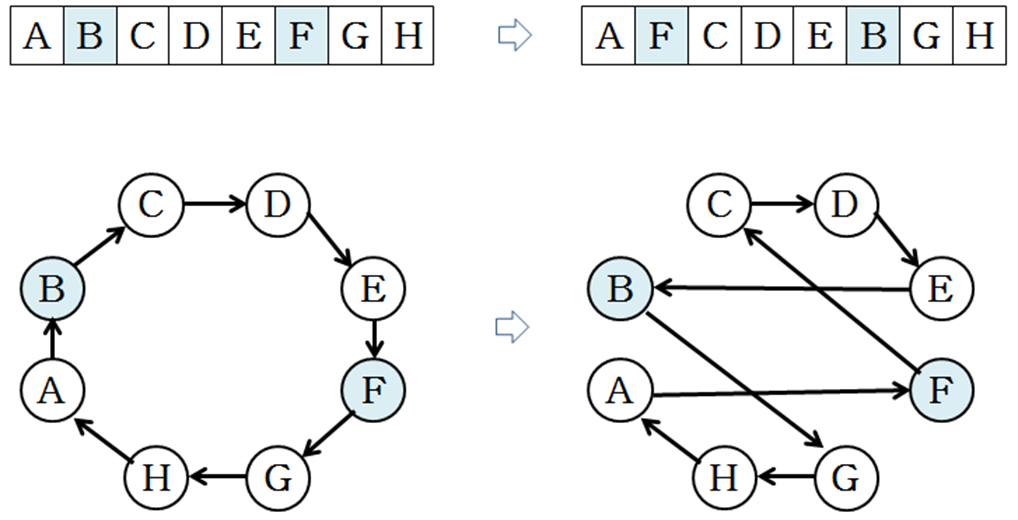
-
반전
- 2개 도시 랜덤 선택
- 선택 도시 + 두 도시 사이의 도시를 역순으로 반전