새싹 인공지능 응용sw 개발자 양성 교육 프로그램 심선조 강사님 수업 정리 글입니다.
런타임 설정 → 연결
gpu가 cpu보다 빠름. gpu 계속 연결하면 안 된다.
집에서는 gpu 연결하는 것 비추
수업 교재: 백견불여일타 딥러닝 입문 with 텐서플로우
!pwd #리눅스 서버에서 우리가 나온 곳, 리눅스 서버, 현재 파일 경로
#리눅스 명령어 앞에 !사용/contentimport pandas as pdpd.read_csv('/content/drive/MyDrive/Colab Notebooks/sesac_deeplerning/bike.csv',encoding='cp949')| datetime | season | holiday | workingday | weather | temp | atemp | humidity | windspeed | casual | registered | count | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 2011-01-01 00:00:00 | 1 | 0 | 0 | 1 | 9.84 | 14.395 | 81 | 0.0000 | 3 | 13 | 16 |
| 1 | 2011-01-01 01:00:00 | 1 | 0 | 0 | 1 | 9.02 | 13.635 | 80 | 0.0000 | 8 | 32 | 40 |
| 2 | 2011-01-01 02:00:00 | 1 | 0 | 0 | 1 | 9.02 | 13.635 | 80 | 0.0000 | 5 | 27 | 32 |
| 3 | 2011-01-01 03:00:00 | 1 | 0 | 0 | 1 | 9.84 | 14.395 | 75 | 0.0000 | 3 | 10 | 13 |
| 4 | 2011-01-01 04:00:00 | 1 | 0 | 0 | 1 | 9.84 | 14.395 | 75 | 0.0000 | 0 | 1 | 1 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 10881 | 2012-12-19 19:00:00 | 4 | 0 | 1 | 1 | 15.58 | 19.695 | 50 | 26.0027 | 7 | 329 | 336 |
| 10882 | 2012-12-19 20:00:00 | 4 | 0 | 1 | 1 | 14.76 | 17.425 | 57 | 15.0013 | 10 | 231 | 241 |
| 10883 | 2012-12-19 21:00:00 | 4 | 0 | 1 | 1 | 13.94 | 15.910 | 61 | 15.0013 | 4 | 164 | 168 |
| 10884 | 2012-12-19 22:00:00 | 4 | 0 | 1 | 1 | 13.94 | 17.425 | 61 | 6.0032 | 12 | 117 | 129 |
| 10885 | 2012-12-19 23:00:00 | 4 | 0 | 1 | 1 | 13.12 | 16.665 | 66 | 8.9981 | 4 | 84 | 88 |
10886 rows × 12 columns
<svg xmlns="http://www.w3.org/2000/svg" height="24px"viewBox="0 0 24 24"
width="24px">
<script>
const buttonEl =
document.querySelector('#df-077866c7-9241-44d6-a098-a8e01792fbd2 button.colab-df-convert');
buttonEl.style.display =
google.colab.kernel.accessAllowed ? 'block' : 'none';
async function convertToInteractive(key) {
const element = document.querySelector('#df-077866c7-9241-44d6-a098-a8e01792fbd2');
const dataTable =
await google.colab.kernel.invokeFunction('convertToInteractive',
[key], {});
if (!dataTable) return;
const docLinkHtml = 'Like what you see? Visit the ' +
'<a target="_blank" href=https://colab.research.google.com/notebooks/data_table.ipynb>data table notebook</a>'
+ ' to learn more about interactive tables.';
element.innerHTML = '';
dataTable['output_type'] = 'display_data';
await google.colab.output.renderOutput(dataTable, element);
const docLink = document.createElement('div');
docLink.innerHTML = docLinkHtml;
element.appendChild(docLink);
}
</script>
</div>import sys #파이썬 버전 확인sys.version'3.8.16 (default, Dec 7 2022, 01:12:13) \n[GCC 7.5.0]'import tensorflow as tftf.__version__'2.9.2'케라스
텐서플로우 1버전 초기 버전(텐서 플로우 그래프에 데이터를 흘려서 사용하는 형태)은 전문적으로 배우지 않으면 사용하기 힘들었음 -> '케라스'라는 라이브러리를 통해 텐서플로우를 처리할 수 있게 되었다. 텐서플로우 2버전은 케라스가 기본 api로 들어가 있음.
sklearn에서는 학습, 예측 틀이 정해져 있어서 편했는데
케라스도 패턴으로 편하게 사용 가능하다.
케라스 특징
- 유연성
- 모듈화
- 파이썬 기반
딥러닝에서 진행하는 내용
1. 학습 데이터 준비
2. 문제를 해결하기 위한 모델 정의
3. 손실 합수, 옵티마이저를 설정
4. 모델을 학습시키고, 추론 -> fit(), evaluate(), predict()
skelearn에서는 평가, 예측 -> predict
케라스에서는 평가 -> evaluate, 예측 -> predict
문제정의
가장 중요한 것은 명확한 문제 정의
-
데이터가 숫자? 문자? 이미지? 오디오?비디오
-
어떻게 해결 이진 분류?다중 분류? 회귀? 생성?
문제 해결을 위한 형태로 데이터를 변경하는 데이터 전처리(data processing) -
손실함수
실제값과 예측값의 차이 계산 = 손실함수
손실함수의 결과값은 작을 수록 좋다.
미분을 통해 계속 작업
과소표집
큰쪽을 작은쪽으로 맞춤
과대표집
작은쪽을 큰쪽으로 맞춤
- 이진분류: 두 개의 범류
- 다중분류: 세 개 이상의 범주로 구분(여러개 중에 하나선택)
- 다중 레이블 분류:여러 개 중에 여러 개 선택
회귀
K폴드
-
하이퍼 파라미터
학습률, 배치 크기, 에폭, 스텝
미분을 통해 w값을 조정
학습률을 크게 잡으면 크게 움직인다.
학습률을 작게 잡으면 작게 움직인다. -
에폭epochs
전체 데이터를 사용하여 학습하는 횟수를 의미
전체 데이터를 10회 반복하여 모델을 학습시킨 것을 10 에폰이라고 한다.
과대적합 - dropout사용
텐서 플로우
기본단위는 넘파이 배열
자료형은 한 가지 형태로만 가질 수 있다.
a = tf.constant(2)print(a) #tf.Tensor(2, shape=(), dtype=int32) : 차원=2tf.Tensor(2, shape=(), dtype=int32)print(tf.rank(a)) #tf.Tensor(0, shape=(), dtype=int32) : 차원=0tf.Tensor(0, shape=(), dtype=int32)b = tf.constant([1,2]) #tf.Tensor(1, shape=(), dtype=int32) :차원=1
print(tf.rank(b))tf.Tensor(1, shape=(), dtype=int32)신경망
- 퍼셉트론
신경망은 퍼셉트론 알고리즘에서부터 시작한다. 퍼셉트론 알고리즘은 여러 개의 신호를 입력받아 하나의 신호를 출력
퍼세트론은 x와 가중치 w를 곱한 값을 모두 더하여 하나의 값(y)으로 만들어 낸다. 이를 임곗값threshold와 비교하여 크면 1, 그렇지 않으면 0을 출력. 이렇게 신경망에서 만들어진 값을 적절한 출력값으로 변환해주는 함수를 활성화 함수라고 한다.
w = 가중치
x = 입력
y = 출력
y = x1w1 + x2w2 + b
- 계단함수step function
단순히 0,1을 출력하는 함수
import tensorflow as tftf.random.set_seed(777)import numpy as np
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD, RMSprop# SGD = 확률적경사하강법
from keras.losses import mse
x = np.array([[0,0],[0,1],[1,0],[1,1]])
y = np.array([[0],[1],[1],[1]])activation : 뉴런의 출력에 적용할 함수
소프트맥스와 같이 뉴련의 선형 방정식 계산 결과에 적용되는 함수를 활성화 함수라고 한다.
input_shape : 입력의 크기
model = Sequential()
model.add(Dense(1,input_shape=(2,),activation='linear')) #Dense : 완전 연결층, 값이 모두 연결되는 것, 입력값 2개 만들고 레이어 하나 만든는데, 레어이의 유닛수가 1이라는 것은 DENCE층을 만들었는데 유닛이 하나다.?
#input_shape=(2,) : 값이 2개가 들어온다. [0,0] 요런 식으로 mnist데이터가 들어올 것이다.
model.compile(optimizer=SGD(),
loss = mse,
metrics=['acc'])
model.fit(x,y,epochs=500) #500번 반복해서 학습하겠다. 계산된 값들은 활성화 함수를 통해서 출력된다.
#우리가 학습에 의해서 찾아야 하는 값은 w, xy는 알고 w값을 찾아야 한다.#가중치 찾기
model.get_weights()
#가중치 array([[0.4478314], #바이어스 b array([0.26910788]
# [0.5199499]][array([[0.4478314],
[0.5199499]], dtype=float32), array([0.26910788], dtype=float32)](0*4478314)+(0*5199499)+0.269107880.26910788(0*4478314)+(1*5199499)+0.269107885199499.26910788(1*4478314)+(0*5199499)+0.269107884478314.26910788(1*4478314)+(1*5199499)+0.269107889677813.26910788#andgate
x = np.array([[0,0],[0,1],[1,0],[1,1]])
y = np.array([[0],[0],[0],[1]])model = Sequential()
model.add(Dense(1,input_shape=(2,),activation='linear')) #Dense : 완전 연결층, 값이 모두 연결되는 것, 입력값 2개 만들고 레이어 하나 만든는데, 레어이의 유닛수가 1이라는 것은 DENCE층을 만들었는데 유닛이 하나다.?
#input_shape=(2,) : 값이 2개가 들어온다. [0,0] 요런 식으로 mnist데이터가 들어올 것이다.
model.compile(optimizer=SGD(),
loss = mse,
metrics=['acc'])
model.fit(x,y,epochs=500) #500번 반복해서 학습하겠다. 계산된 값들은 활성화 함수를 통해서 출력된다.
#우리가 학습에 의해서 찾아야 하는 값은 w, xy는 알고 w값을 찾아야 한다.model.get_weights()[array([[0.53026605],
[0.40107936]], dtype=float32), array([-0.20928293], dtype=float32)](0*0.53026605)+(0*40107936)-0.20928293-0.20928293(0*0.53026605)+(1*40107936)-0.2092829340107935.79071707(1*0.53026605)+(0*40107936)-0.209282930.32098312000000007(1*0.53026605)+(1*40107936)-0.2092829340107936.32098312#nand(and+not)
and
0 0 0 1
00 01 10 11
nand
1 1 1 0
#nandgate
x = np.array([[0,0],[0,1],[1,0],[1,1]])
y = np.array([[1],[1],[1],[0]])model = Sequential()
model.add(Dense(1,input_shape=(2,),activation='linear')) #Dense : 완전 연결층, 값이 모두 연결되는 것, 입력값 2개 만들고 레이어 하나 만든는데, 레어이의 유닛수가 1이라는 것은 DENCE층을 만들었는데 유닛이 하나다.?
#input_shape=(2,) : 값이 2개가 들어온다. [0,0] 요런 식으로 mnist데이터가 들어올 것이다.
model.compile(optimizer=SGD(),
loss = mse,
metrics=['acc'])
model.fit(x,y,epochs=500)model.get_weights()[array([[-0.46928743],
[-0.46345294]], dtype=float32), array([1.2101102], dtype=float32)](0*-0.46928743)+(0*-0.46345294)+1.21011021.2101102(0*-0.46928743)+(1*-0.46345294)+1.21011020.7466572599999999(1*-0.46928743)+(0*-0.46345294)+1.21011020.7408227699999999(1*-0.46928743)+(1*-0.46345294)+1.21011020.27736982999999993#exculsive or
0 1 1 0
00 01 10 11#exculsive or
x = np.array([[0,0],[0,1],[1,0],[1,1]])
y = np.array([[0],[1],[1],[0]])model = Sequential()
model.add(Dense(1,input_shape=(2,),activation='linear'))
model.compile(optimizer=SGD(),
loss = mse,
metrics=['acc'])
model.fit(x,y,epochs=1000)model.get_weights()[array([[-0.02017852],
[-0.02132003]], dtype=float32), array([0.52461153], dtype=float32)](0*-0.02017852)+(0*-0.02132003)+0.524611530.52461153(0*-0.02017852)+(1*-0.02132003)+0.524611530.5032915(1*-0.02017852)+(0*-0.02132003)+0.524611530.5044330100000001(1*-0.02017852)+(1*-0.02132003)+0.524611530.48311298다중 퍼셉트론
x = np.array([[0,0],[0,1],[1,0],[1,1]])
y = np.array([[0],[1],[1],[0]])model = Sequential()
model.add(Dense(32,input_shape=(2,),activation='relu'))
model.add(Dense(1,activation='linear'))
model.compile(optimizer=SGD(),
loss = mse,
metrics=['acc'])
model.fit(x,y,epochs=500)model.get_weights()model.predict(x)1/1 [==============================] - 0s 76ms/step
array([[0.2550785 ],
[0.86930585],
[0.7930248 ],
[0.14710155]], dtype=float32)https://www.youtube.com/watch?v=aircAruvnKk
minst 데이터를 이용한 신경망 설명
활성화 함수
계산해서 다음으로 넘어갈 때 통과한다.
시그모이드 함수는 0~1사이의 값으로 출력된다.
하이퍼볼릭 탄제느 함수
-1~1 근접하지만 -1,1의 값이 되지는 않는다.
ReLU 함수
가장 효과 좋음
-값은 다 0
1 -> 1
2 ->
양수 들어오는 값들은 그대로 쓰고 -값은 다 0으로 처리
신경망
mnist, fashion이 hello world랑 비슷함
from keras.datasets.mnist import load_data(x_train, y_train), (x_test, y_test) = load_data()load_data(path) 리턴 타입
Returns:
Tuple of NumPy arrays: (x_train, y_train), (x_test, y_test).
x_train: uint8 NumPy array of grayscale image data with shapes
(60000, 28, 28), containing the training data. Pixel values range
from 0 to 255.
y_train: uint8 NumPy array of digit labels (integers in range 0-9)
with shape (60000,) for the training data.
x_test: uint8 NumPy array of grayscale image data with shapes
(10000, 28, 28), containing the test data. Pixel values range
from 0 to 255.
y_test: uint8 NumPy array of digit labels (integers in range 0-9)
with shape (10000,) for the test data.
x_train.shape(60000, 28, 28)x_test.shape(10000, 28, 28)y_train[:5]array([5, 0, 4, 1, 9], dtype=uint8)import matplotlib.pyplot as plt
import numpy as npsample_size=3
random_idx = np.random.randint(60000,size=sample_size)
random_idxarray([53515, 17627, 21886])for idx in random_idx:
img = x_train[idx,:]
label = y_train[idx]
plt.imshow(img)
plt.title(f'{idx}-th data, label is {label}')
x_train[0].min()0x_train[0].max()255from sklearn.model_selection import train_test_splitx_train,x_val,y_train,y_val = train_test_split(x_train,
y_train,
test_size=0.3,
random_state=777)
print(x_train.shape,y_train.shape)(42000, 28, 28) (42000,)- 전처리
[0] = index0 = 데이터 건수
#일차원으로 만들기
x_train = (x_train.reshape((-1,28*28)))/255
x_train.shape(42000, 784)#0~1사이의 값으로 변환까지 완료
x_train.min(),x_train.max()(0.0, 1.0)#일차원으로 만들기
x_val = (x_val.reshape((-1,28*28)))/255
x_test = (x_test.reshape((-1,28*28)))/255- 모델 입력을 위한 레이블 전처리
원핫인코딩 많이 사용
from keras.utils import to_categorical
이미지는 흑백으로 그레이스스케일 사용
모양만들기(일차원 만들기)
0~1사이 값으로 만들기
from keras.utils import to_categoricaly_train = to_categorical(y_train)
y_val = to_categorical(y_val)
y_test = to_categorical(y_test)array([[0., 0., 1., ..., 0., 0., 0.], ->2번째
[0., 0., 0., ..., 1., 0., 0.], ->7번째
[0., 0., 0., ..., 0., 0., 0.],
...,
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.]], dtype=float32)
- 모델 구성하기
from keras.models import Sequential #가장 기본적 형태
from keras.layers import Dense #완전연결층, 기본적 형태#모델을 만들고, 데이터 모델에 추가
model = Sequential()
#처음에는 들어 올 때 몇 개로 들어와야 하는 지 정해야 한다.
model.add(Dense(64,activation='relu',input_shape=(784,))) #64 = 1층의 유닛수, 입력은 784(28*28)개, w도 784개, 유닛당 바이어스b 붙어있음
#유닛 수 = 784(입력)*64(Dense층)+64(바이어스)
model.add(Dense(32,activation='relu'))
model.add(Dense(10,activation='softmax')) #10개로 나가고, softmax=나가는 값 전체 합을 구하면 1(=100%) , 값이 제일 큰 게 정답이 된다. 입력 2가 들어가면 2가될 확률이 가장 높게 나오는 값이 정답이 된다.
#마지막은 나갈 때 몇 개로 나가야 하는 지 정해야 한다.
모델을 만들었고 complie하기
model.compile(optimizer='adam', #상황에 따라 나가야 하는 형태가 정해져 있다
loss='categorical_crossentropy',metrics=['acc']) #metrics=['acc'] 정확도로 평가하겠다.
#loss는 최종값이 원핫인코딩으로 만들어지면 'categorical_crossentropy, gd : 경사하강법, 모든 데이터를 검토해서 시간이 오래 걸린다.
sgd : 데이터 일부만 가지고 빨리 계산한다.
스텐사이즈는 학습률을 봐야 한다.
adagrad : 기울기가 급하면 학습률을 크게크게 듬성듬성 건너가고
기울기가 완만하면 학습률을 작게작게 조금조금 움직이자
RMSProp : 조금움직이만 이전 맥락도 봐가면서 가자
momentrum : 스텝 계산해서 움직이는 데 내려오면 방향으로 또 가자
adam : 가장 많이 쓰임, 분위가 보면서 보폭도 줄이고 더 가봄
옵티마이저의 역할은 오차가 가장 작은 지점을 찾아간다. 제대로 찾아갈 수 있게끔 여러가지 방법들이 있다.
history = model.fit(x_train,y_train,
epochs=30,
batch_size=128,
validation_data=(x_val,y_val)#중간 결과값 저장 42000을 30으로 나누면 스텝스가 되고, 한 번 돌면 ?
) Epoch 1/30
329/329 [==============================] - 2s 5ms/step - loss: 0.5245 - acc: 0.8475 - val_loss: 0.2457 - val_acc: 0.9313
Epoch 2/30
329/329 [==============================] - 1s 4ms/step - loss: 0.2001 - acc: 0.9429 - val_loss: 0.1792 - val_acc: 0.9487
Epoch 3/30
329/329 [==============================] - 1s 4ms/step - loss: 0.1495 - acc: 0.9570 - val_loss: 0.1554 - val_acc: 0.9553
Epoch 4/30
329/329 [==============================] - 1s 4ms/step - loss: 0.1198 - acc: 0.9653 - val_loss: 0.1354 - val_acc: 0.9606
Epoch 5/30
329/329 [==============================] - 1s 4ms/step - loss: 0.1022 - acc: 0.9698 - val_loss: 0.1239 - val_acc: 0.9646
Epoch 6/30
329/329 [==============================] - 1s 4ms/step - loss: 0.0868 - acc: 0.9739 - val_loss: 0.1364 - val_acc: 0.9597
Epoch 7/30
329/329 [==============================] - 1s 4ms/step - loss: 0.0762 - acc: 0.9774 - val_loss: 0.1237 - val_acc: 0.9638
Epoch 8/30
329/329 [==============================] - 1s 4ms/step - loss: 0.0659 - acc: 0.9806 - val_loss: 0.1110 - val_acc: 0.9671
Epoch 9/30
329/329 [==============================] - 1s 4ms/step - loss: 0.0577 - acc: 0.9824 - val_loss: 0.1100 - val_acc: 0.9671
Epoch 10/30
329/329 [==============================] - 1s 4ms/step - loss: 0.0517 - acc: 0.9844 - val_loss: 0.1045 - val_acc: 0.9702
Epoch 11/30
329/329 [==============================] - 1s 4ms/step - loss: 0.0472 - acc: 0.9864 - val_loss: 0.1056 - val_acc: 0.9697
Epoch 12/30
329/329 [==============================] - 1s 4ms/step - loss: 0.0423 - acc: 0.9874 - val_loss: 0.1063 - val_acc: 0.9701
Epoch 13/30
329/329 [==============================] - 1s 4ms/step - loss: 0.0351 - acc: 0.9899 - val_loss: 0.1123 - val_acc: 0.9684
Epoch 14/30
329/329 [==============================] - 1s 4ms/step - loss: 0.0340 - acc: 0.9896 - val_loss: 0.1073 - val_acc: 0.9696
Epoch 15/30
329/329 [==============================] - 1s 4ms/step - loss: 0.0287 - acc: 0.9917 - val_loss: 0.1100 - val_acc: 0.9686
Epoch 16/30
329/329 [==============================] - 1s 4ms/step - loss: 0.0241 - acc: 0.9936 - val_loss: 0.1194 - val_acc: 0.9671
Epoch 17/30
329/329 [==============================] - 1s 4ms/step - loss: 0.0223 - acc: 0.9941 - val_loss: 0.1133 - val_acc: 0.9697
Epoch 18/30
329/329 [==============================] - 1s 4ms/step - loss: 0.0202 - acc: 0.9952 - val_loss: 0.1131 - val_acc: 0.9698
Epoch 19/30
329/329 [==============================] - 1s 4ms/step - loss: 0.0178 - acc: 0.9953 - val_loss: 0.1200 - val_acc: 0.9697
Epoch 20/30
329/329 [==============================] - 1s 4ms/step - loss: 0.0156 - acc: 0.9960 - val_loss: 0.1138 - val_acc: 0.9711
Epoch 21/30
329/329 [==============================] - 2s 5ms/step - loss: 0.0139 - acc: 0.9966 - val_loss: 0.1232 - val_acc: 0.9693
Epoch 22/30
329/329 [==============================] - 3s 8ms/step - loss: 0.0124 - acc: 0.9965 - val_loss: 0.1271 - val_acc: 0.9689
Epoch 23/30
329/329 [==============================] - 2s 7ms/step - loss: 0.0121 - acc: 0.9967 - val_loss: 0.1284 - val_acc: 0.9708
Epoch 24/30
329/329 [==============================] - 1s 4ms/step - loss: 0.0122 - acc: 0.9967 - val_loss: 0.1388 - val_acc: 0.9678
Epoch 25/30
329/329 [==============================] - 1s 4ms/step - loss: 0.0112 - acc: 0.9969 - val_loss: 0.1318 - val_acc: 0.9698
Epoch 26/30
329/329 [==============================] - 1s 4ms/step - loss: 0.0072 - acc: 0.9985 - val_loss: 0.1343 - val_acc: 0.9702
Epoch 27/30
329/329 [==============================] - 1s 4ms/step - loss: 0.0068 - acc: 0.9985 - val_loss: 0.1342 - val_acc: 0.9714
Epoch 28/30
329/329 [==============================] - 1s 4ms/step - loss: 0.0063 - acc: 0.9985 - val_loss: 0.1495 - val_acc: 0.9688
Epoch 29/30
329/329 [==============================] - 1s 4ms/step - loss: 0.0099 - acc: 0.9972 - val_loss: 0.1513 - val_acc: 0.9686
Epoch 30/30
329/329 [==============================] - 1s 4ms/step - loss: 0.0114 - acc: 0.9962 - val_loss: 0.1570 - val_acc: 0.9676history<keras.callbacks.History at 0x7f2694d46dc0>history.history.keys() #값확인dict_keys(['loss', 'acc', 'val_loss', 'val_acc'])그래프로 그려보기
import matplotlib.pyplot as plthis_dict = history.history
loss = his_dict['loss']
val_loss = his_dict['val_loss']
epochs = range(1,len(loss)+1) #range 연속된 숫자가 필요해서 range사용
fig = plt.figure(figsize=(10,5))
ax1 = fig.add_subplot(1,2,1)#1행의 2열 첫 번째이다.
ax1.plot(epochs, loss, color='blue', label='train_loss')
ax1.plot(epochs,val_loss,color='orange',label='val_loss')
ax1.legend()
<matplotlib.legend.Legend at 0x7f269044a130>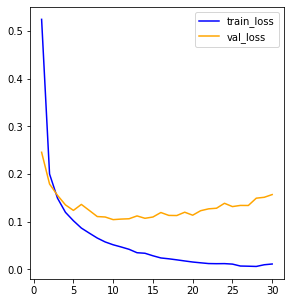
model.evaluate(x_test,y_test)his_dict = history.history
loss = his_dict['loss']
val_loss = his_dict['val_loss']
epochs = range(1,len(loss)+1) #range 연속된 숫자가 필요해서 range사용
fig = plt.figure(figsize=(10,5))
ax1 = fig.add_subplot(1,2,1)#1행의 2열 첫 번째이다.
ax1.plot(epochs, loss, color='blue', label='train_loss')
ax1.plot(epochs,val_loss,color='orange',label='val_loss')
ax1.legend()
acc = his_dict['acc']
val_acc = his_dict['val_acc']
ax2 = fig.add_subplot(1,2,2)#1행의 2열 첫 번째이다.
ax2.plot(epochs, acc, color='blue', label='train_acc')
ax2.plot(epochs, val_acc,color='orange',label='val_acc')
ax2.legend()<matplotlib.legend.Legend at 0x7f2692a05fd0>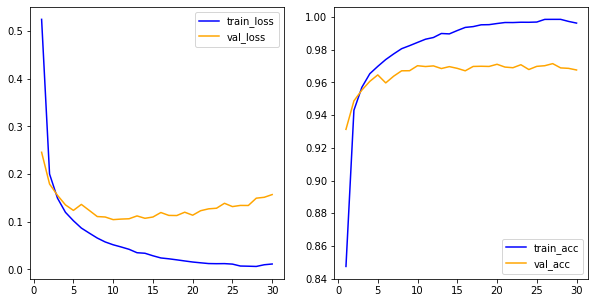
과대적합: 세밀하게 분석, 정확도가 떨어진다
과대적합 문제가 나타나면 데이터 특성, 모델 구조 등을 수정해보고 재학습
model.evaluate(x_test,y_test) #정확도:0.9700999855995178313/313 [==============================] - 1s 2ms/step - loss: 0.1467 - acc: 0.9701
[0.14666560292243958, 0.9700999855995178]#예측
results = model.predict(x_test)#결과313/313 [==============================] - 1s 2ms/stepresults.shape(10000, 10)results[0] #확률array([2.4063402e-11, 2.1041620e-15, 5.7191365e-08, 2.0876705e-05,
1.8434040e-19, 5.8375954e-10, 5.0120952e-27, 9.9997884e-01,
1.1448843e-07, 9.5394647e-08], dtype=float32)np.round(results[0],2)array([0., 0., 0., 0., 0., 0., 0., 1., 0., 0.], dtype=float32)np.argmax(results[0])7y_test[0]array([0., 0., 0., 0., 0., 0., 0., 1., 0., 0.], dtype=float32)x_test[0]array([0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0.32941176, 0.7254902 , 0.62352941,
0.59215686, 0.23529412, 0.14117647, 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0.87058824, 0.99607843, 0.99607843, 0.99607843, 0.99607843,
0.94509804, 0.77647059, 0.77647059, 0.77647059, 0.77647059,
0.77647059, 0.77647059, 0.77647059, 0.77647059, 0.66666667,
0.20392157, 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0.2627451 , 0.44705882,
0.28235294, 0.44705882, 0.63921569, 0.89019608, 0.99607843,
0.88235294, 0.99607843, 0.99607843, 0.99607843, 0.98039216,
0.89803922, 0.99607843, 0.99607843, 0.54901961, 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0.06666667, 0.25882353, 0.05490196, 0.2627451 ,
0.2627451 , 0.2627451 , 0.23137255, 0.08235294, 0.9254902 ,
0.99607843, 0.41568627, 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0.3254902 , 0.99215686, 0.81960784, 0.07058824,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0.08627451, 0.91372549,
1. , 0.3254902 , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0.50588235, 0.99607843, 0.93333333, 0.17254902,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0.23137255, 0.97647059,
0.99607843, 0.24313725, 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0.52156863, 0.99607843, 0.73333333, 0.01960784,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0.03529412, 0.80392157,
0.97254902, 0.22745098, 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0.49411765, 0.99607843, 0.71372549, 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0.29411765, 0.98431373,
0.94117647, 0.22352941, 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0.0745098 , 0.86666667, 0.99607843, 0.65098039, 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0.01176471, 0.79607843, 0.99607843,
0.85882353, 0.1372549 , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0.14901961, 0.99607843, 0.99607843, 0.30196078, 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0.12156863, 0.87843137, 0.99607843,
0.45098039, 0.00392157, 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0.52156863, 0.99607843, 0.99607843, 0.20392157, 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0.23921569, 0.94901961, 0.99607843,
0.99607843, 0.20392157, 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0.4745098 , 0.99607843, 0.99607843, 0.85882353, 0.15686275,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0.4745098 , 0.99607843,
0.81176471, 0.07058824, 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ])plt.imshow(x_test[0].reshape(28,28),cmap='gray')<matplotlib.image.AxesImage at 0x7f2692846be0>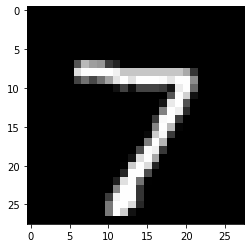
#구글드라이브데이터 가져와 예측, 결과값 적용해보기
import glob
from PIL import Image#패턴을 학습한 것이 아닌 그 위치를 학습한 거라 랜덤포레스트와 비슷하다.
for path in glob.glob('/content/drive/MyDrive/Colab Notebooks/sesac_deeplerning/03_mnist_img/*.png'):
img = Image.open(path).convert('L')
img = np.resize(img,(1,784))
result = (255-img)/255 #0~1사이의 값으로 만들어줌
#print(result.min(),result.max())
plt.imshow(result.reshape(28,28),cmap='gray') #ndarray형태라서 reshape사용
plt.show()
pred = model.predict(result)
print(np.round(pred, 3))
print(np.argmax(pred))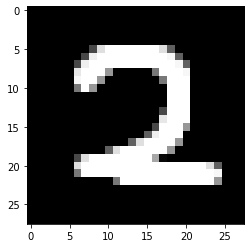
1/1 [==============================] - 0s 18ms/step
[[0. 1. 0. 0. 0. 0. 0. 0. 0. 0.]]
1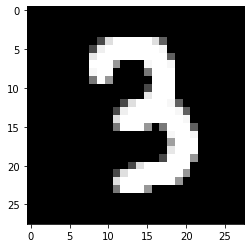
1/1 [==============================] - 0s 17ms/step
[[0. 0. 1. 0. 0. 0. 0. 0. 0. 0.]]
2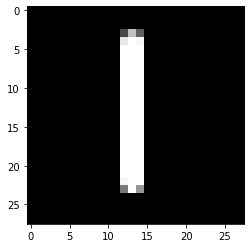
1/1 [==============================] - 0s 16ms/step
[[0. 0. 0. 1. 0. 0. 0. 0. 0. 0.]]
3
1/1 [==============================] - 0s 17ms/step
[[0. 0. 0. 0. 0.023 0. 0. 0. 0.953 0.024]]
8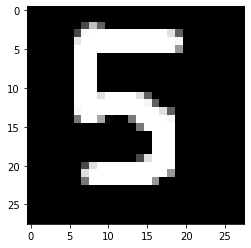
1/1 [==============================] - 0s 20ms/step
[[0. 0. 0. 0. 0. 0. 0. 0. 1. 0.]]
8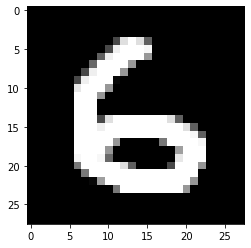
1/1 [==============================] - 0s 17ms/step
[[0. 0. 0. 0. 0. 0. 1. 0. 0. 0.]]
6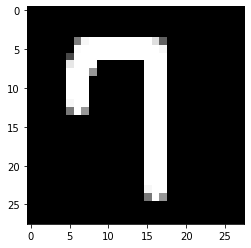
1/1 [==============================] - 0s 18ms/step
[[0. 0. 0.023 0.002 0. 0. 0. 0. 0.976 0. ]]
8
1/1 [==============================] - 0s 16ms/step
[[0. 0. 0. 0. 0. 0.207 0.793 0. 0. 0. ]]
6
1/1 [==============================] - 0s 17ms/step
[[0. 0. 0.002 0.002 0. 0. 0. 0. 0.996 0. ]]
8
1/1 [==============================] - 0s 17ms/step
[[0.879 0. 0.03 0. 0. 0. 0. 0. 0. 0.092]]
0model.save('mnist.h5') #일체형으로 파일저장from keras.models import load_modelnew_model = load_model('mnist.h5')np.argmax(new_model.predict(x_test)[0])313/313 [==============================] - 1s 3ms/step
7#가중치만 저장
model.save_weights('mnist')model1 = Sequential()
model1.add(Dense(64,activation='relu',input_shape=(784,)))
model1.add(Dense(32,activation='relu'))
model1.add(Dense(10,activation='softmax'))model1.load_weights('mnist')<tensorflow.python.training.tracking.util.CheckpointLoadStatus at 0x7f2692c7d700>np.argmax(model1.predict(x_test)[0])313/313 [==============================] - 1s 2ms/step
7