[Python] 백준 / RGB거리 / 1149번 / DP

DP 개념 바로가기

문제

RGB거리 문제 링크

RGB거리에는 집이 N개 있다. 거리는 선분으로 나타낼 수 있고, 1번 집부터 N번 집이 순서대로 있다.

집은 빨강, 초록, 파랑 중 하나의 색으로 칠해야 한다. 각각의 집을 빨강, 초록, 파랑으로 칠하는 비용이 주어졌을 때, 아래 규칙을 만족하면서 모든 집을 칠하는 비용의 최솟값을 구해보자.

• 1번 집의 색은 2번 집의 색과 같지 않아야 한다.
• N번 집의 색은 N-1번 집의 색과 같지 않아야 한다.
• i(2 ≤ i ≤ N-1)번 집의 색은 i-1번, i+1번 집의 색과 같지 않아야 한다.

입력

첫째 줄에 집의 수 N(2 ≤ N ≤ 1,000)이 주어진다. 둘째 줄부터 N개의 줄에는 각 집을 빨강, 초록, 파랑으로 칠하는 비용이 1번 집부터 한 줄에 하나씩 주어진다. 집을 칠하는 비용은 1,000보다 작거나 같은 자연수이다.

3
26 40 83
49 60 57
13 89 99

출력

첫째 줄에 모든 집을 칠하는 비용의 최솟값을 출력한다.

96

접근 방식

현재 RGB중 한 색을 선택했다면 그 이전은 현재 색을 제외한 비용 중 작은 비용을 선택한다

1. 3차원 배열로 입력을 받는다

2. 반복문을 통해 각 색을 선택했을 때 현재 색을 제외한 다른 색 중 최소 비용을 선택하여 현재 값과 더한다

3. 마지막 리스트 중 가장 적은 비용을 선택하여 출력한다

코드

# url : https://www.acmicpc.net/problem/1149
# 난이도 : silver 1

import sys
n = int(input())

num_lists = [list(map(int,sys.stdin.readline().split())) for _ in range(n)]


# 이 전에 칠한 색을 제외한 비용 중 작은 값을 현재 비용과 더한다
for i in range(1, len(num_lists)):
    num_lists[i][0] += min(num_lists[i-1][1],num_lists[i-1][2])
    num_lists[i][1] += min(num_lists[i-1][0],num_lists[i-1][2])
    num_lists[i][2] += min(num_lists[i-1][0],num_lists[i-1][1])

print(min(num_lists[n-1]))
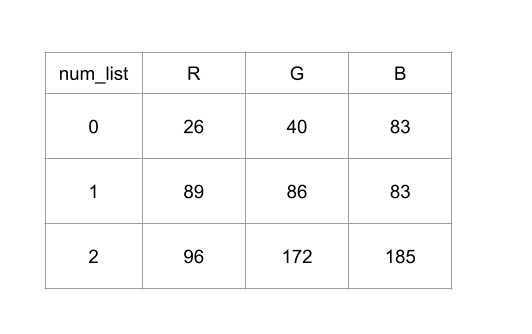
print(num_lists)