[알고리즘 개념] 동적계획법 (Dynamic Programming)

동적 계획법 (Dynamic Programming)

동적 계획법(DP)은 메모리를 적절히 사용하여 수행 시간 효율성을 향상시키는 방법이다

• 이미 계산된 결과를 별도의 메모리 영역에 저장하여 중복계산을 막는다
• 다이나믹 프로그래밍의 구현은 일반적으로 두가지 방식(top-down , bottom-up)으로 구성된다

문제가 다음과 같은 조건일 때 동적 계획법을 사용할 수 있다

• 최적 부분 구조(Optimal Substructure)
  - 큰 문제를 작은 문제로 나눌 수 있으며 작은 문제의 답을 모아 큰 문제를 해결할 수 있다
• 중복되는 부분 문제(Overlapping Subproblem)
  - 동일한 작은 문제를 반복적으로 해결해야 한다

피보나치 수열의 일반적인 재귀 풀이

• fibo함수가 얼마나 실행되는지 확인하는 코드를 추가

def fibo(n):
    print(f'fibo({n})', end=' ')
                        
    if n == 1 or n == 2 :
        return 1
    
    return fibo(n-1) + fibo(n-2)

print(fibo(5))

• 실행결과
  

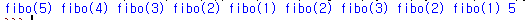
• 시간 복잡도 : 함수 하나가 두개를 반환하므로 O(2^n)
  

피보나치 수열의 동적계획법 (top-down) 풀이

• Memoization
  - 한번 계산한 결과를 메모리 공간에 저장하는 기법
  - 같은 문제를 다시 호출하면 저장된 결과를 그대로 가져온다
• 결과 저장용 리스트를 DP테이블이라 부른다

#DP table
d = [0] * 100

def fibo(n):
    print(f'fibo({n})', end=' ')

                   
    if n == 1 or n == 2 :
        return 1

    if d[n] != 0:
        return d[n]

    d[n] = fibo(n-1) + fibo(n-2)
    return d[n]

print(fibo(5))

• 실행결과 ( fibo(1) 이후의 fibo함수는 DP table에 대응되는 수를 바로 반환 )
  

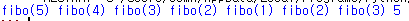
• 시간 복잡도 : O(n)

피보나치 수열의 동적계획법(bottom-up) 풀이

#DP table
d = [0] * 100


d[1] = 1
d[2] = 1
n = 5

for i in range(3, n+1):
    d[i] = d[i - 1] + d[i - 2]

print(d[n])

• 실행 결과

출처
https://www.youtube.com/watch?v=5Lu34WIx2Us